Graphing Functions (DP IB Maths: AA HL)

Revision Note

Author

Dan

Last updated

20 April 2023

Did this video help you?

Graphing Functions

How do I graph the function y = f(x)?

A point $(a, b)$ lies on the graph $y = f (x)$ if $f (a) = b$
The horizontal axis is used for the domain
The vertical axis is used for the range
You will be able to graph some functions by hand
For some functions you will need to use your GDC
You might be asked to graph the sum or difference of two functions
- Use your GDC to graph $y = f (x) + g (x)$ or $y = f (x) - g (x)$
- Just type the functions into the graphing mode

What is the difference between “draw” and “sketch”?

If asked to sketch you should:
- Show the general shape
- Label any key points such as the intersections with the axes
- Label the axes
If asked to draw you should:
- Use a pencil and ruler
- Draw to scale
- Plot any points accurately
- Join points with a straight line or smooth curve
- Label any key points such as the intersections with the axes
- Label the axes

How can my GDC help me sketch/draw a graph?

You use your GDC to plot the graph
- Check the scales on the graph to make sure you see the full shape
Use your GDC to find any key points
Use your GDC to check specific points to help you plot the graph

Did this video help you?

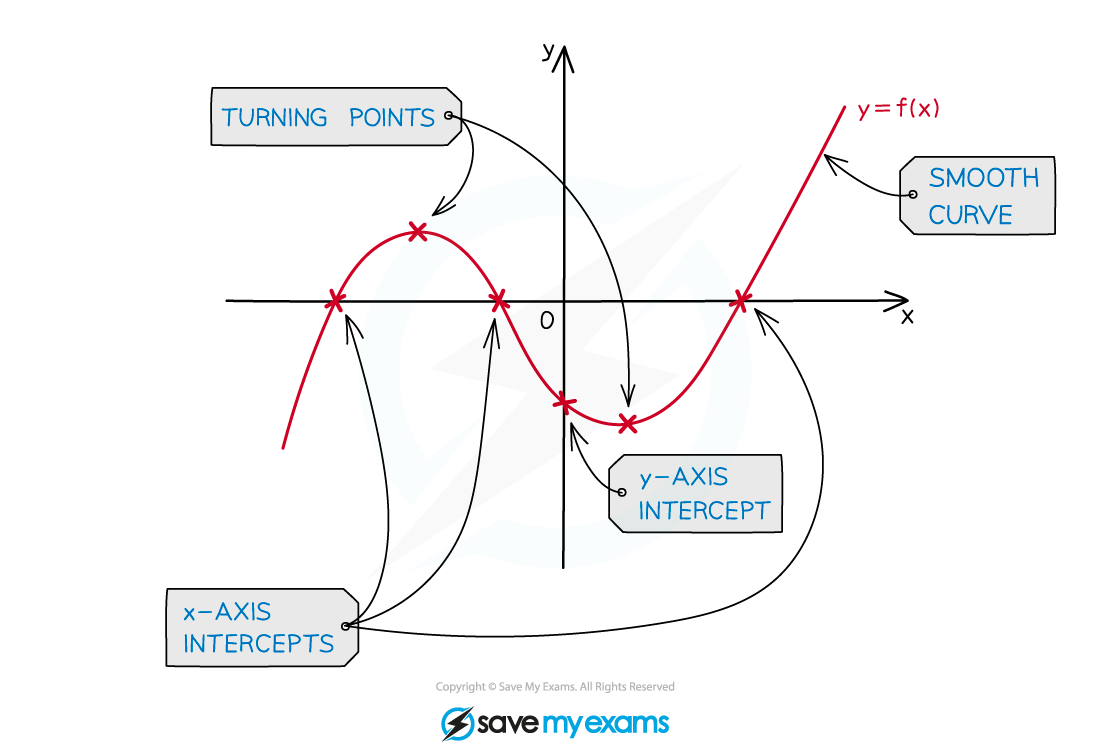
Key Features of Graphs

What are the key features of graphs?

You should be familiar with the following key features and know how to use your GDC to find them
Local minimums/maximums
- These are points where the graph has a minimum/maximum for a small region
- They are also called turning points
  - This is where the graph changes its direction between upwards and downwards directions
- A graph can have multiple local minimums/maximums
- A local minimum/maximum is not necessarily the minimum/maximum of the whole graph
  - This would be called the global minimum/maximum
- For quadratic graphs the minimum/maximum is called the vertex
Intercepts
- y – intercepts are where the graph crosses the y-axis
  - At these points x = 0
- x – intercepts are where the graph crosses the x-axis
  - At these points y = 0
  - These points are also called the zeros of the function or roots of the equation
Symmetry
- Some graphs have lines of symmetry
  - A quadratic will have a vertical line of symmetry
Asymptotes
- These are lines which the graph will get closer to but not cross
- These can be horizontal or vertical
  - Exponential graphs have horizontal asymptotes
  - Graphs of variables which vary inversely can have vertical and horizontal asymptotes

Sketching Polynomials Notes Diagram 1

Examiner Tip

Most GDC makes/models will not plot/show asymptotes just from inputting a function
- Add the asymptotes as additional graphs for your GDC to plot
- You can then check the equations of your asymptotes visually
- You may have to zoom in or change the viewing window options to confirm an asymptote
Even if using your GDC to plot graphs and solve problems sketching them as part of your working is good exam technique
- Label the key features of the graph and anything else relevant to the question on your sketch

Worked example

Two functions are defined by

$f (x) = x^{2} - 4 x - 5$ and $g (x) = 2 + \frac{1}{x + 1}$ .

Draw the graph

y = f (x)

2-2-2-ib-ai-key-features-of-graphs-a-we-solution

Sketch the graph

y = g (x)

2-2-2-ib-ai-key-features-of-graphs-b-we-solution

Did this video help you?

Intersecting Graphs

How do I find where two graphs intersect?

Plot both graphs on your GDC
Use the intersect function to find the intersections
Check if there is more than one point of intersection

Solving Equations Graphically Notes Diagram 1

How can I use graphs to solve equations?

One method to solve equations is to use graphs
To solve $f (x) = a$
- Plot the two graphs $y = f (x)$ and $y = a$ on your GDC
- Find the points of intersections
- The x-coordinates are the solutions of the equation
To solve $f (x) = g (x)$
- Plot the two graphs $y = f (x)$ and $y = g (x)$ on your GDC
- Find the points of intersections
- The x-coordinates are the solutions of the equation
Using graphs makes it easier to see how many solutions an equation will have

Examiner Tip

You can use graphs to solve equations
- Questions will not necessarily ask for a drawing/sketch or make reference to graphs
- Use your GDC to plot the equations and find the intersections between the graphs

Worked example

Two functions are defined by

$f (x) = x^{3} - x$ and $g (x) = \frac{4}{x}$ .

Sketch the graph

y = f (x)

2-2-2-ib-ai-sl-intersecting-graphs-a-we-solution

Write down the number of real solutions to the equation

x^{3} - x = 2

2-2-2-ib-ai-sl-intersecting-graphs-b-we-solution

Find the coordinates of the points where

y = f (x)

and

y = g (x)

intersect.

2-2-2-ib-ai-sl-intersecting-graphs-c-we-solution

Write down the solutions to the equation

x^{3} - x = \frac{4}{x}

2-2-2-ib-ai-sl-intersecting-graphs-d-we-solution

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself Flashcards

Did this page help you?

Previous:2.3.3 Symmetry of FunctionsNext:2.4.1 Exponential & Logarithmic Functions

Graphing Functions (DP IB Maths: AA HL)

Revision Note

How do I graph the function y = f(x)?

What is the difference between “draw” and “sketch”?

How can my GDC help me sketch/draw a graph?

What are the key features of graphs?

How do I find where two graphs intersect?

How can I use graphs to solve equations?

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

1. Number & Algebra

1.1 Number & Algebra Toolkit

1.1.1 Standard Form

1.1.2 Laws of Indices

1.1.3 Partial Fractions

1.2 Exponentials & Logs

1.2.1 Introduction to Logarithms

1.2.2 Laws of Logarithms

1.2.3 Solving Exponential Equations

1.3 Sequences & Series

1.3.1 Language of Sequences & Series

1.3.2 Arithmetic Sequences & Series

1.3.3 Geometric Sequences & Series

1.3.4 Applications of Sequences & Series

1.3.5 Compound Interest & Depreciation

1.4 Simple Proof & Reasoning

1.4.1 Proof

1.5 Further Proof & Reasoning

1.5.1 Proof by Induction

1.5.2 Proof by Contradiction

1.6 Binomial Theorem

1.6.1 Binomial Theorem

1.6.2 Extension of The Binomial Theorem

1.7 Permutations & Combinations

1.7.1 Counting Principles

1.7.2 Permutations & Combinations

1.8 Complex Numbers

1.8.1 Intro to Complex Numbers

1.8.2 Modulus & Argument

1.8.3 Introduction to Argand Diagrams

1.9 Further Complex Numbers

1.9.1 Geometry of Complex Numbers

1.9.2 Forms of Complex Numbers

1.9.3 Complex Roots of Polynomials

1.9.4 De Moivre's Theorem

1.9.5 Roots of Complex Numbers

1.10 Systems of Linear Equations

1.10.1 Systems of Linear Equations

1.10.2 Algebraic Solutions

2. Functions

2.1 Linear Functions & Graphs

2.1.1 Equations of a Straight Line

2.2 Quadratic Functions & Graphs

2.2.1 Quadratic Functions

2.2.2 Factorising & Completing the Square

2.2.3 Solving Quadratics

2.2.4 Quadratic Inequalities

2.2.5 Discriminants

2.3 Functions Toolkit

2.3.1 Language of Functions

2.3.2 Composite & Inverse Functions

2.3.3 Symmetry of Functions

2.3.4 Graphing Functions

2.4 Other Functions & Graphs

2.4.1 Exponential & Logarithmic Functions

2.4.2 Solving Equations

2.4.3 Modelling with Functions

2.5 Reciprocal & Rational Functions

2.5.1 Reciprocal & Rational Functions

2.6 Transformations of Graphs

2.6.1 Translations of Graphs

2.6.2 Reflections of Graphs

2.6.3 Stretches Graphs

2.6.4 Composite Transformations of Graphs

2.7 Polynomial Functions

2.7.1 Factor & Remainder Theorem

2.7.2 Polynomial Division

2.7.3 Polynomial Functions

2.7.4 Roots of Polynomials