Roots of Complex Numbers (DP IB Analysis & Approaches (AA)): Revision Note
Did this video help you?
Roots of complex numbers
How do I find the square roots of a complex number?
A complex number
has two square roots,
and
, that are also complex
To find them, let
where
and form simultaneous equations from the relationship
by expanding
and equating the real and imaginary parts with
E.g. find the square roots of
Let
be one of the square roots of
This means
Expand the left-hand side
so
Equate the real parts on both sides
Equate the imaginary parts on both sides
Solve these two equations simultaneously
e.g. make
the subject of
to get
Substitute
into
to get
Rearrange to
which gives
or
(but
)
so
which gives
The two square roots are
and
How do I use de Moivre’s theorem to find the nth roots of a complex number?
De Moivre's theorem to find the
th roots of a complex number,
, is
Letting
gives each
th root
In exponential (Euler's) form, this is
where
Examiner Tips and Tricks
This formula is not given in the formula booklet so it must be learnt.
e.g. find the fourth roots of
gives
gives
gives
gives
Examiner Tips and Tricks
Your GDC can find roots of complex numbers.
How are complex roots related to polygons?
If you plot the
complex roots of of a complex number on an Argand diagram
they form a regular
-sided polygon
e.g. in the example above
,
,
and
form a square
whose vertices lies on a circle of radius
Worked Example
(a) Find both square roots of , giving your answers in the form
.
Answer:

(b) Solve the equation , giving your solutions in the form
.
Answer:
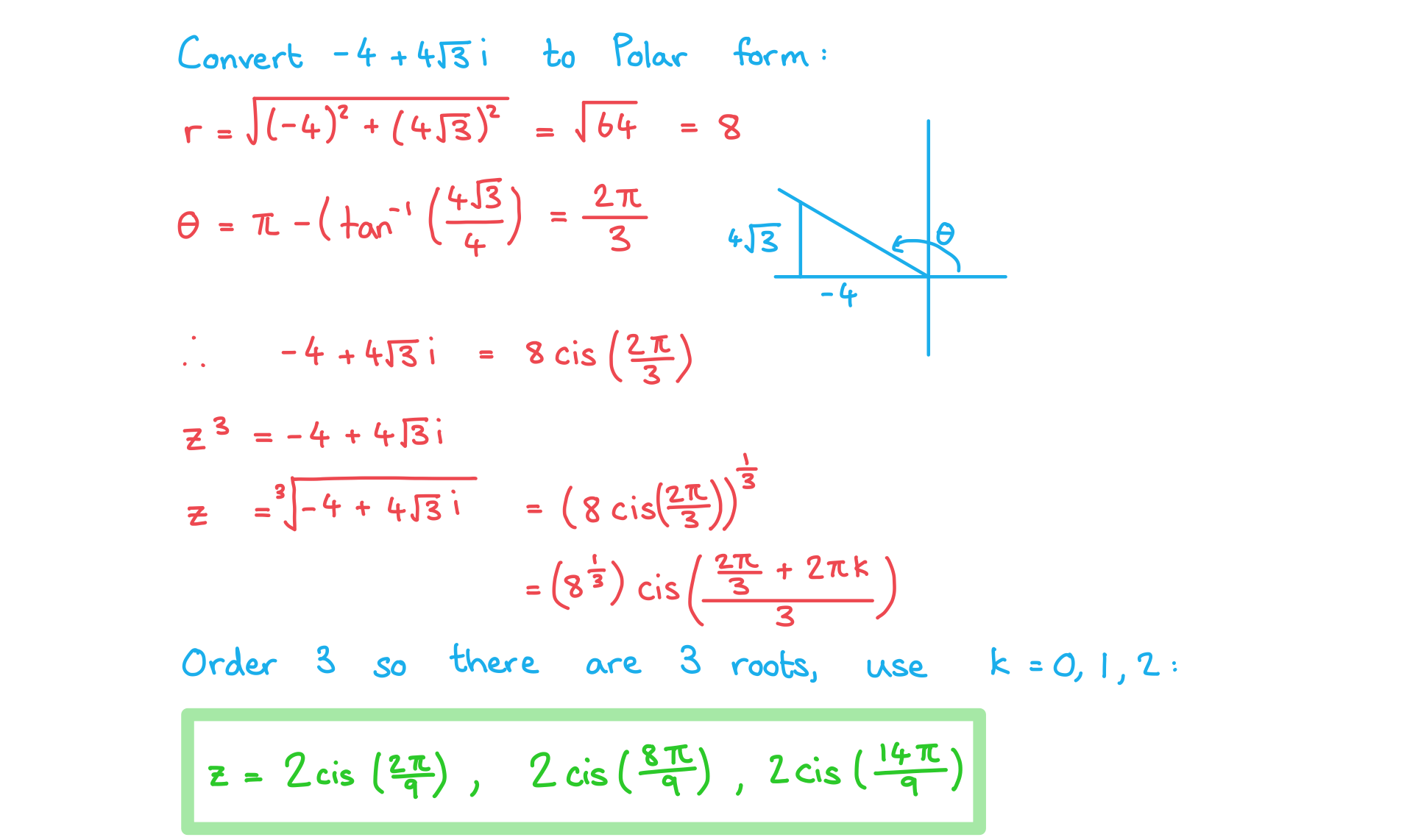

Unlock more, it's free!
Did this page help you?