Roots of Complex Numbers (DP IB Analysis & Approaches (AA)) : Revision Note
Did this video help you?
Roots of Complex Numbers
How do I find the square root of a complex number?
The square roots of a complex number will themselves be complex:
i.e. if
then
We can then square (
) and equate it to the original complex number (
), as they both describe
:
Then expand and simplify:
As both sides are equal we are able to equate real and imaginary parts:
Equating the real components:
(1)
Equating the imaginary components:
(2)
These equations can then be solved simultaneously to find the real and imaginary components of the square root
In general, we can rearrange (2) to make
and then substitute into (1)
This will lead to a quartic equation in terms of d; which can be solved by making a substitution to turn it into a quadratic
The values of
can then be used to find the corresponding values of
, so we now have both components of both square roots (
)
Note that one root will be the negative of the other root
g.
and
How do I use de Moivre’s Theorem to find roots of a complex number?
De Moivre’s Theorem states that a complex number in modulus-argument form can be raised to the power of n by
Raising the modulus to the power of n and multiplying the argument by n
When in modulus-argument (polar) form de Moivre’s Theorem can then be used to find the roots of a complex number by
Taking the nth root of the modulus and dividing the argument by n
If
then
Recall that adding 2π to the argument of a complex number does not change the complex number
Therefore we must consider how different arguments will give the same result
This can be rewritten as
This can be written in exponential (Euler’s) form as
For
,
The nth root of complex number will have n roots with the properties:
The modulus is
for all roots
There will be n different arguments spaced at equal intervals on the unit circle
This creates some geometrically beautiful results:
The five roots of a complex number raised to the power 5 will create a regular pentagon on an Argand diagram
The eight roots of a complex number raised to the power 8 will create a regular octagon on an Argand diagram
The n roots of a complex number raised to the power n will create a regular n-sided polygon on an Argand diagram
Sometimes you may need to use your GDC to find the roots of a complex number
Using your GDC’s store function will help when entering complicated modulus and arguments
Make sure you choose the correct form to enter your complex number in
Your GDC should be able to give you the answer in your preferred form
Examiner Tips and Tricks
De Moivre's theorem makes finding roots of complex numbers very easy, but you must be confident converting from Cartesian form into Polar and Euler's form first
If you are in a calculator exam your GDC will be able to do this for you but you must clearly show how you got to your answer
You must also be prepared to do this by hand in a non-calculator paper
Worked Example
a) Find the square roots of 5 + 12i, giving your answers in the form a + bi.

b) Solve the equation giving your answers in the form r cis θ.
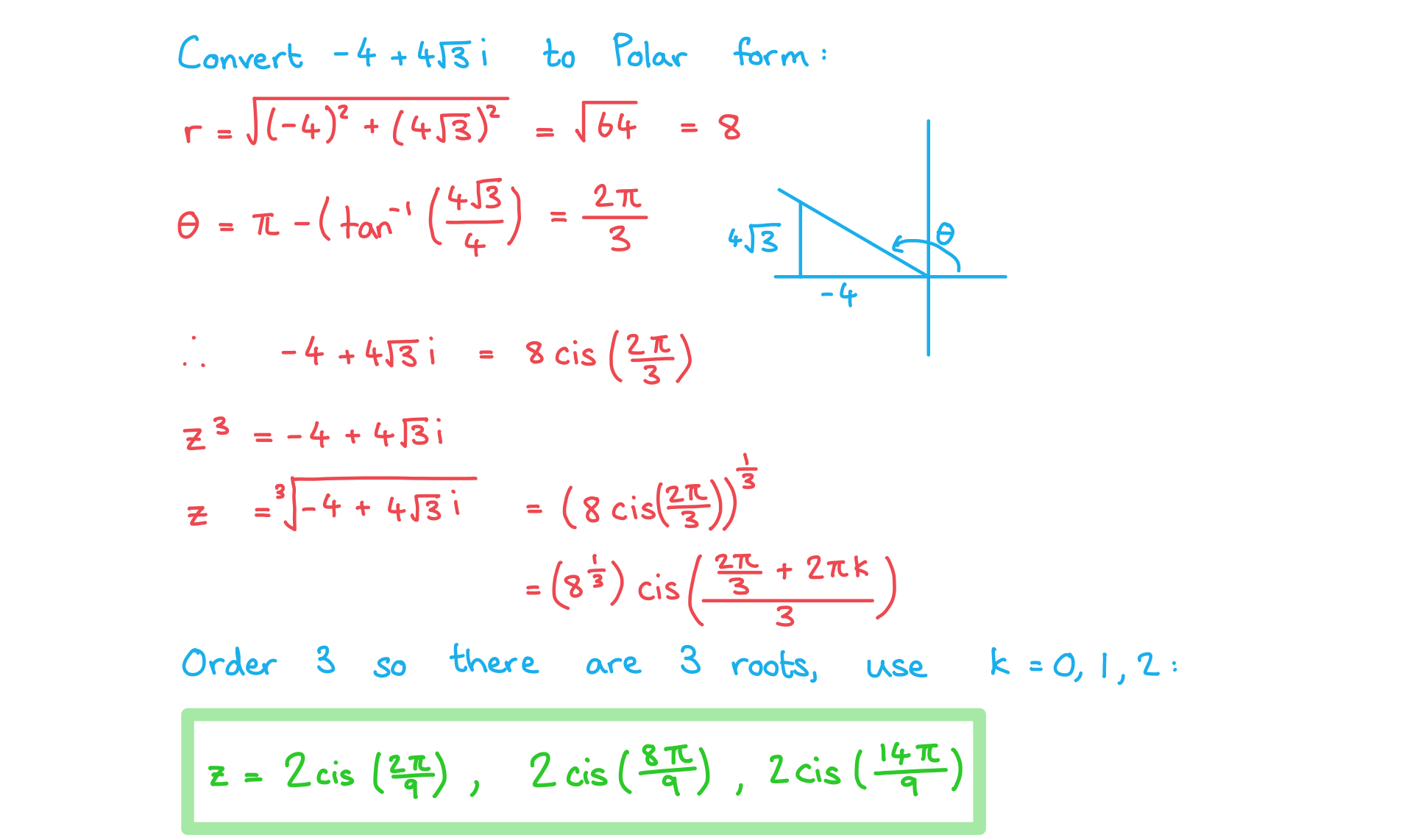

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?
