Volumes of Revolution (DP IB Analysis & Approaches (AA)): Revision Note

Volumes of Revolution Around x-axis

What is a volume of revolution around the x-axis?

• A solid of revolution is formed when an area bounded by a function
  (and other boundary equations) is rotated radians around the -axis

• The volume of revolution is the volume of this solid

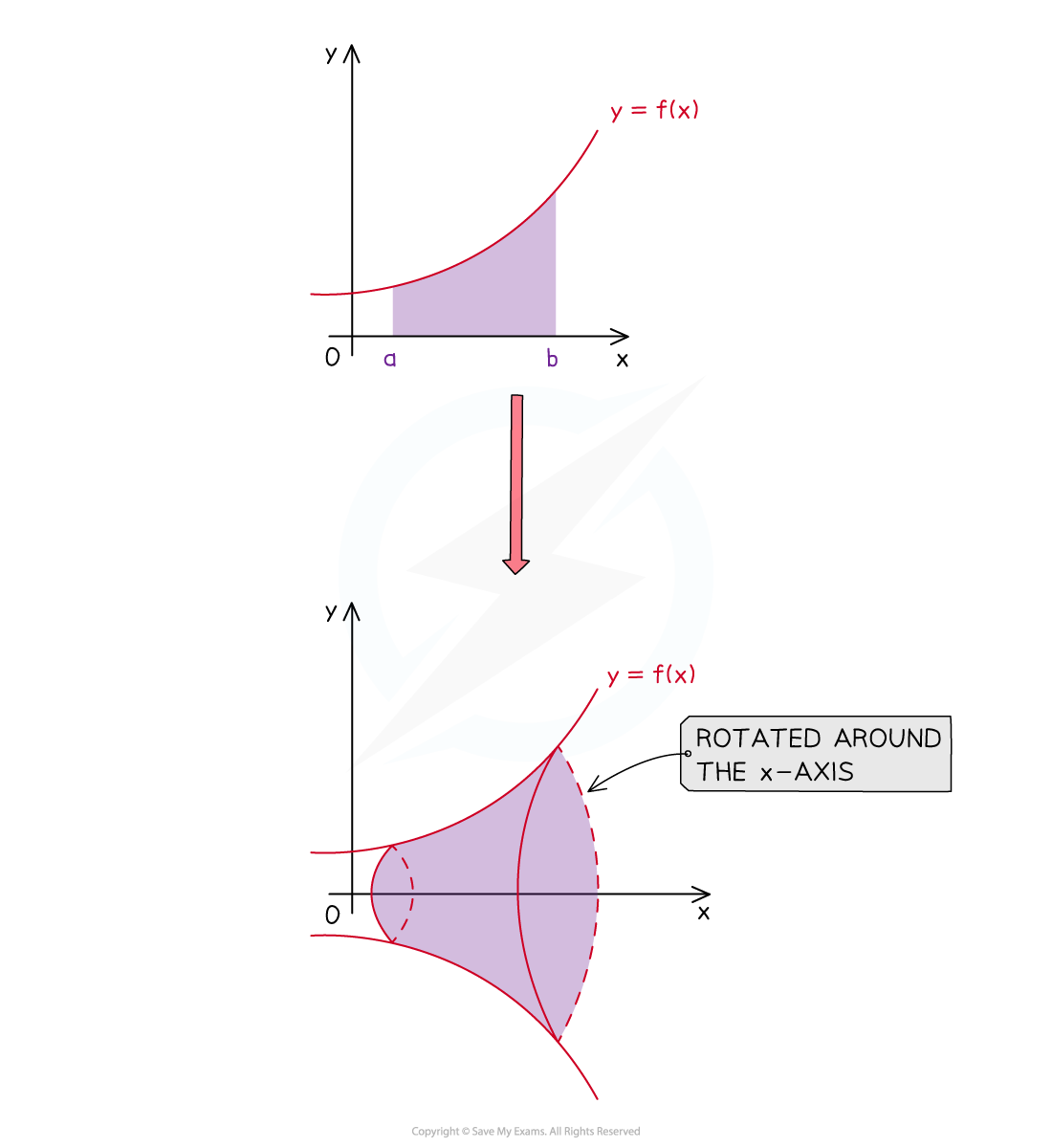
• Be careful – the ’front’ and ‘back’ of this solid are flat

  • They were created from straight (vertical) lines

  • 3D sketches can be misleading

How do I solve problems involving a volume of revolution around x-axis?

• Use the formula

• is a function of

• and are the equations of the (vertical) lines bounding the area

  • If and are not stated in a question, the boundaries could involve the -axis () and/or a root of

  • You can use a GDC to plot the curve, sketch it and highlight the area to help

  • Visualising the solid created is helpful

    • Try sketching some functions and their solids of revolution for practice

• STEP 1
  Identify the limits and

  • Sketching the graph of or using a GDC to do so is helpful, especially when  and are not given directly in the question
     

• STEP 2
  Square the function
   

• STEP 3
  Use the formula to evaluate the integral and find the volume of revolution

  • An answer may be required in exact form

Volumes of Revolution Around y-axis

What is a volume of revolution around the y-axis?

• Very similar to above, this is a solid of revolution which is formed when an area bounded by a function (and other boundary equations) is rotated radians  around the -axis

• The volume of revolution is the volume of this solid

How do I solve problems involving a volume of revolution around the y-axis?

• Use the formula

•  is a function of 

  • the function is usually given in the form 

  • this will need rearranging into the form

• and  are the equations of the (horizontal) lines bounding the area

  • If  and  are not stated in the question, the boundaries could involve the -axis () and/or a root of

  • Use a GDC to plot the curve, sketch it and highlight the area for practice

  • Visualising the solid created is helpful

    • Try sketching some functions and their solids of revolution to help

• STEP 1
  Identify the limits and 

  • Sketching the graph of or using a GDC to do so is helpful, especially if and  are not given directly in the question

• STEP 2
  Rearrange into the form 

  • This is similar to finding the inverse function

• STEP 3
  Square the function
   

• STEP 4
  Use the formula to evaluate the integral and find the volume of revolution

  • An answer may be required in exact form