Applying Techniques in Chemistry (DP IB Chemistry)
Revision Note
Applying Techniques in Chemistry
There are a number of practical experiments and techniques that you need to be aware of, within the following categories:
Volumetric analysis techniques
Separation techniques
Purification techniques
Other techniques and experiments
Volumetric analysis
Volumetric analysis techniques including:
Preparing a standard solution
Carrying out dilutions
Performing titrations (acid–base titration and redox titration)
Volumetric analysis is a process that uses the volume and concentration of one chemical reactant (a standard / volumetric solution) to determine the concentration of another unknown solution
The technique most commonly used is a titration
The volumes are measured using two precise pieces of equipment:
A volumetric or graduated pipette
A burette
Before the titration can be done, the standard solution must be prepared
Specific apparatus must be used both when preparing the standard solution and when completing the titration, to ensure that volumes are measured precisely
Key pieces of apparatus used to prepare a volumetric solution and perform a simple titration
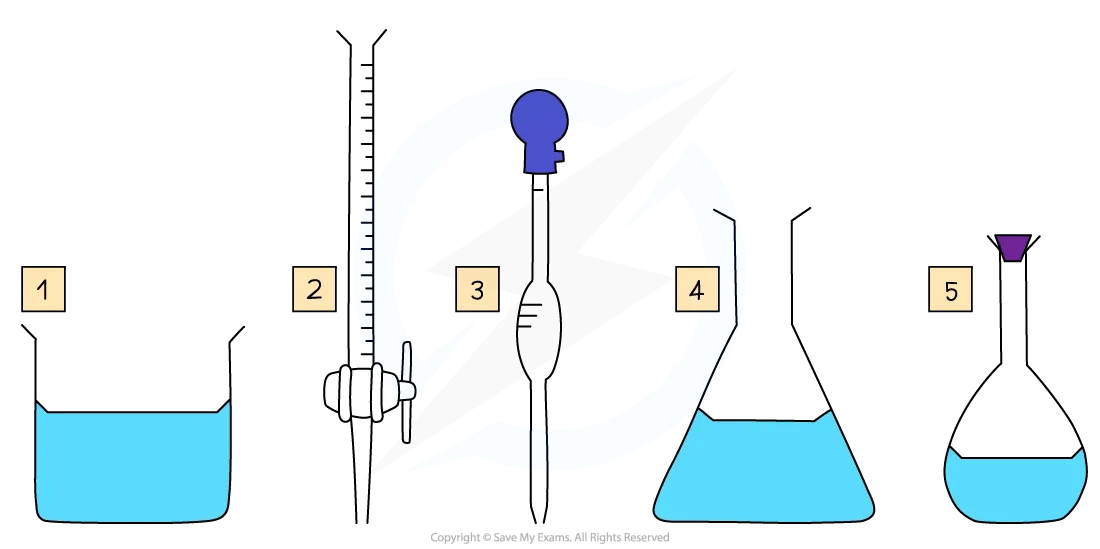
Key pieces of apparatus for volumetric analysis include a beaker, burette, volumetric pipette, conical flask and a standard / volumetric flask
Making a standard / volumetric solution
Chemists routinely prepare solutions needed for analysis, whose concentrations are known precisely
These solutions are termed standard solutions or volumetric solutions
They are made as accurately and precisely as possible using three decimal place balances and volumetric flasks to reduce the impact of measurement uncertainties
How to prepare a standard solution
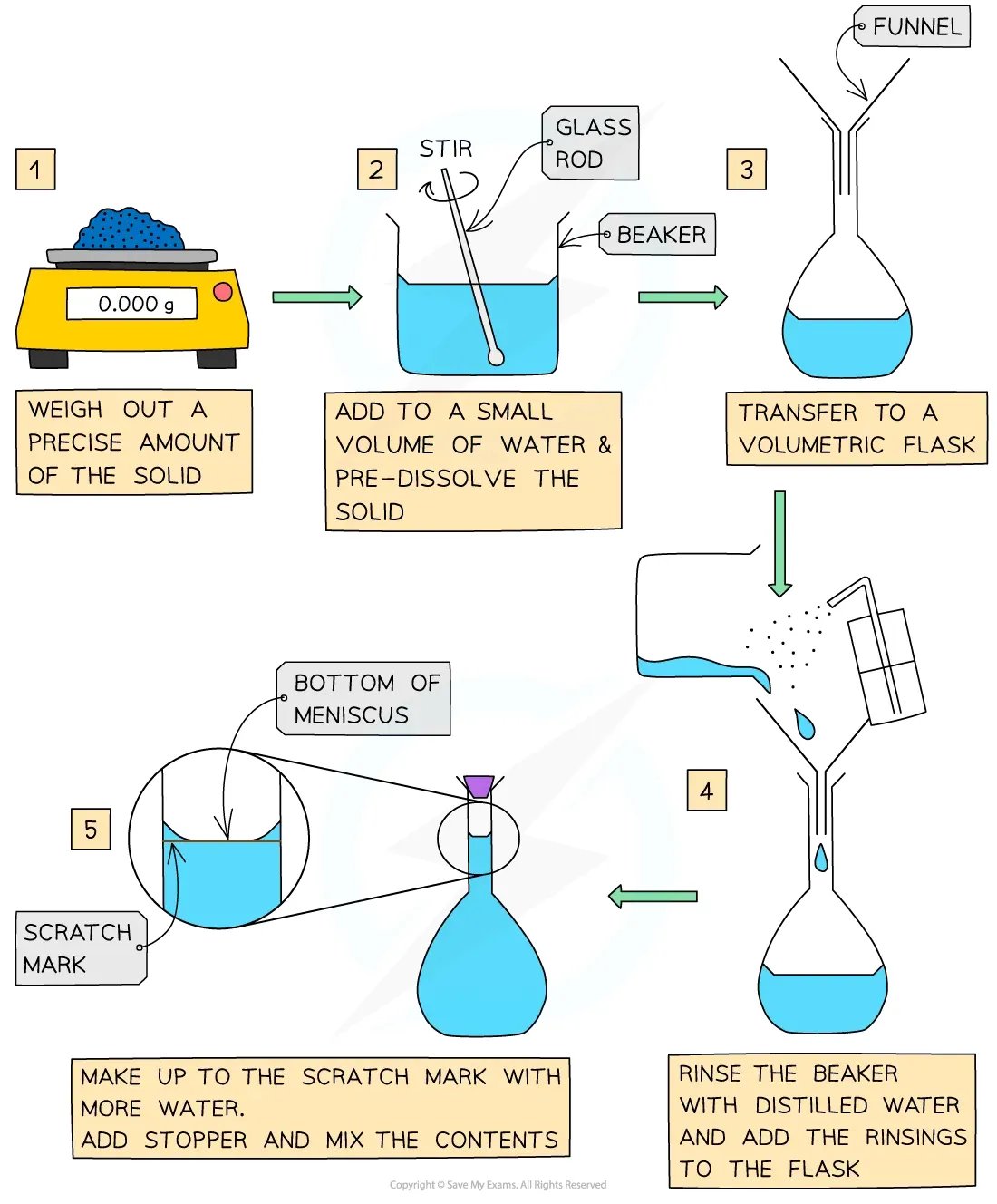
A standard solution is made by adding a measured mass of solid to a measured volume of deionised water
Worked Example
Calculate the mass of sodium hydroxide, NaOH, required to prepare 250 cm3 of a 0.200 mol dm-3 solution.
Answer:
Find the number of moles of NaOH needed from the concentration and volume:
number of moles = concentration (mol dm-3) x volume (dm3)
n = 0.200 mol dm–3 x 0.250 dm3
n = 0.0500 mol
Find the molar mass of NaOH:
Mr = 22.99 + 16.00 + 1.01 = 40.00 g mol–1
Calculate the mass of NaOH required:
mass = moles x molar mass
mass = 0.0500 mol x 40.00 g mol–1 = 2.00 g
Carrying out dilutions
The concentration of a solution is the amount of solute dissolved in a solvent to make 1 dm3 of solution
The solute is the substance that dissolves in a solvent to form a solution
The solvent is often water
A concentrated solution is a solution that has a high concentration of solute
A dilute solution is a solution with a low concentration of solute
Concentration is usually expressed in one of three ways:
moles per unit volume
mass per unit volume
parts per million
A concentrated solution can be diluted to form a dilute solution
For example, diluting 500 cm3 of a stock 1.0 mol dm–3 standard solution to a 0.5 mol dm–3 standard solution
Take the 500 cm3 of the 1.0 mol dm–3 standard solution
Add 500 cm3 of deionised water
There is now 1000 cm3 of a 0.5 mol dm–3 standard solution
Serial dilutions are a sequence of dilutions
The initial stock solution is typically diluted by a factor of 10, e.g. 100 cm3 of the stock solution added to 900 cm3 of deionised solution
This process is then repeated until a solution of the desired concentration is achieved
Performing titrations
Titrations include acid-base titrations and redox titrations
Acid-base titrations involve an acid and a base
Redox titrations are more specific reactions involving the reduction and oxidation occurring simultaneously, e.g. the Fe2+ / MnO4– titration
The key piece of equipment used in the titration is the burette
Burettes are usually marked to a precision of 0.10 cm3
Since they are analogue instruments, the uncertainty is recorded to half the smallest marking, in other words to ±0.05 cm3
The endpoint or equivalence point occurs when the two solutions have reacted completely
In the case of most acid-base titrations, this can be observed with the use of an indicator
For more information about choosing indicators, see our revision note on Choosing an Acid-Base Indicator
There are some examples of redox titrations where no indicator is required, e.g. the Fe2+ / MnO4– redox titration
Using an indicator in titrations
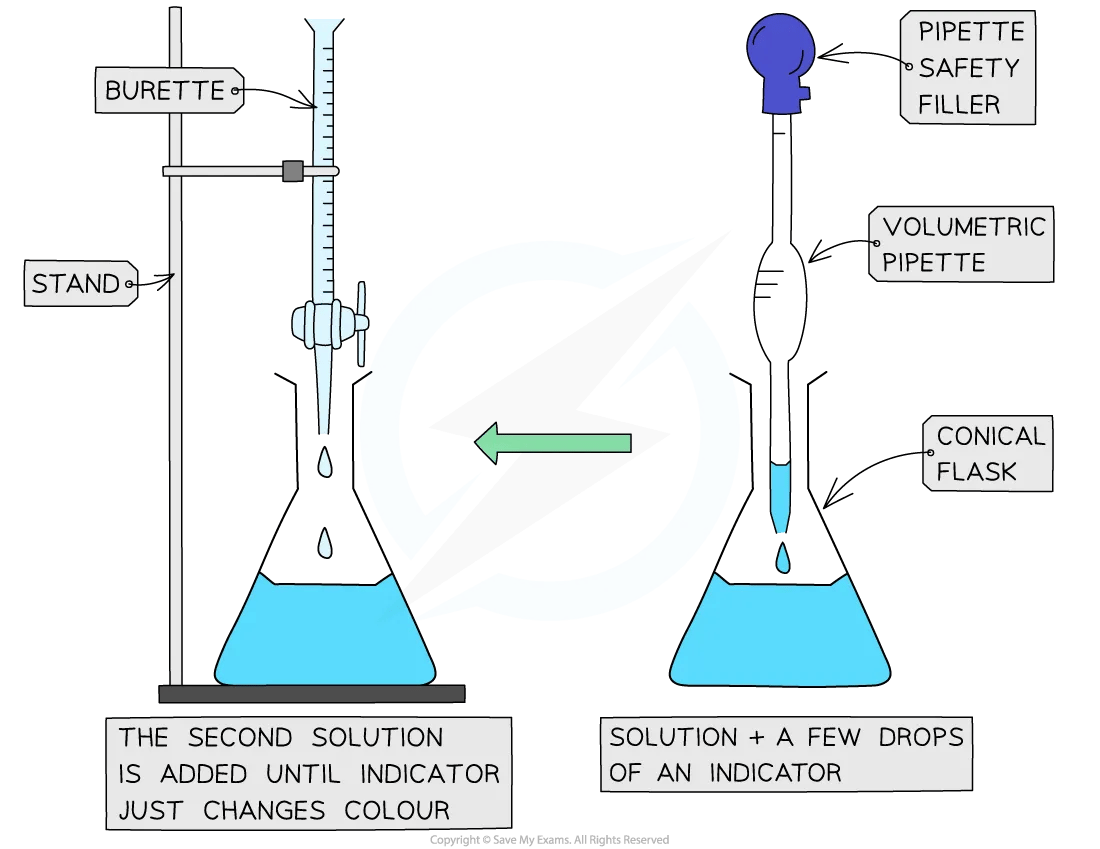
Only a few drops of indicator are added, if necessary, because they are typically weak acids and can influence the results
The steps in a titration are:
Measuring a known volume (usually 20.0 or 25.0 cm3) of one of the solutions with a volumetric pipette and placing it into a conical flask
The other solution is placed in the burette
To start with, the burette will usually be filled to 0.00 cm3
If necessary, a few drops of indicator are added to the solution in the conical flask
A white tile is sometimes placed under the conical flask while the titration is performed, to make it easier to see the colour change
The tap on the burette is carefully opened and the solution is added, portion by portion, to the conical flask until the indicator starts to change colour
After each portion, the conical flask should be swirled
As you start getting near to the endpoint, the flow of the burette should be slowed right down so that the solution is added dropwise
You should be able to close the tap on the burette after one drop has caused a permanent colour change
Multiple runs are carried out until concordant results are obtained
Recording and processing titration results
Both the initial and final burette readings should be recorded and shown to a precision of ±0.05 cm3, the same as the uncertainty
A typical layout and set of titration results
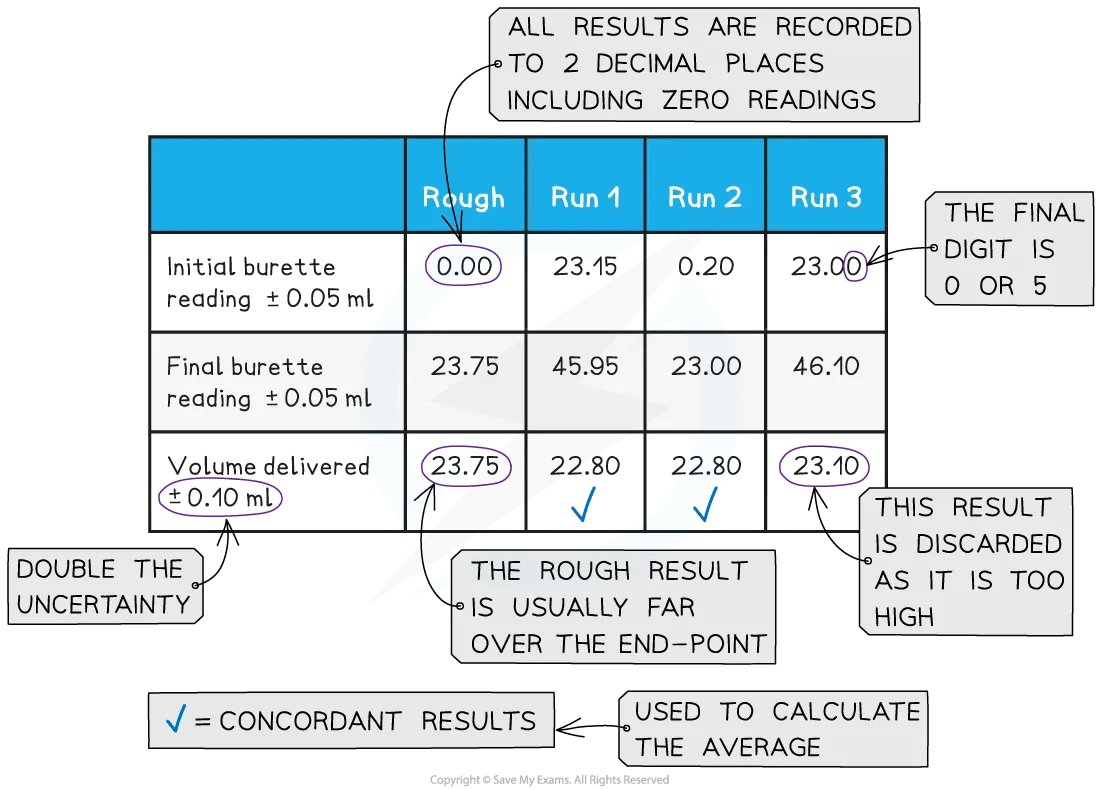
The volume delivered (titre) is calculated and recorded to an uncertainty of ±0.10 cm3
For more information about working with uncertainties, see our revision note on Processing Uncertainties in Chemistry
Concordant results are then averaged, and non-concordant results are discarded
For more information about calculating average titres, see "What is the mean average?" in our Applying General Mathematics in Chemistry revision note
Appropriate titration calculations are then performed, as shown in our revision note on Concentration Calculations
Separation of mixtures
The required separation techniques covered in our revision note on Separating Mixtures include:
Filtration
Simple and fractional distillation
Paper chromatography
The process of thin layer chromatography is the same as paper chromatography
The stationary phase is changed from chromatography paper to a sheet with a fine layer of silica or alumina
The mobile phase can still be any liquid solvent
Separation is still based on solubility
It can be common to use UV light or locating agents, such as ninhydrin, to identify the spots
Crystallisation
Purification techniques
The specific purification techniques explicitly stated in the syllabus are:
Recrystallisation
Melting point determination
Recrystallisation
Recrystallisation involves dissolving an impure solid in a suitable solvent and then allowing the compound to crystallise out of the solution
The recrystallisation product should have a higher purity
This process relies on the differences in solubility between the desired compound and the impurities present in the original solid
For more information about recrystallisation, see our revision note on Separating Mixtures
Melting point determination
The melting point of a solid is indicative of its purity and identity
A melting point can be matched to a known substance as a means of identification or confirmation of a desired product
The proximity of a melting point to the actual data book value can express purity
Impurities tend to lower the melting point of a solid
The melting point range also reveals the degree of purity
Pure substances have sharp well-defined melting points
Impure substances have a broad melting point range, i.e. a large difference between when the substance first melts and when it completely melts
The skills needed in performing a melting point test are largely dependent on the specific melting point apparatus you are using:
Different apparatus used to determine the melting point of a sample
|
However, there are some common key skills:
Correctly preparing the melting point tubes
Heating the tubes very slowly
Repeating to get a range of measurements (three would be normal)
The sample solid must be totally dry and finely powdered - this can be achieved by crushing it with the back of a spatula onto some filter paper or the back of a white tile (this absorbs any moisture)
Use the first tube to find the approximate melting point range and then repeat using a much slower heating rate
Other experiments and techniques
Other specific experiments and techniques explicitly stated in the syllabus are:
Calorimetry
For more information about calorimetry, see our revision note on Calorimetry
Electrochemical cells
For more information about experiments involving electrochemical cells, see the relevant revision notes in our Electron Transfer Reactions topic
Drying to constant mass
Reflux
Colorimetry / spectrophotometry
Physical and digital molecular modelling
Drying to constant mass
This is used to determine the amount of water (or volatile components) in a substance
The initial mass of the substance is recorded, using a balance
The substance is placed in an oven / drying chamber and heated at a specific temperature
At regular intervals, the substance is taken out of the oven, allowed to cool and reweighed
These steps are repeated until the recorded mass of the substance remains constant
This is a common technique associated with water of crystallisation in hydrated transition metal compounds
Heating under reflux
Organic reactions often occur slowly at room temperature
Therefore, organic reactions can be completed by heating under reflux to produce an organic liquid
This allows the mixture to react as fully as possible without the loss of any reactants, products or solvent
In distillation, you are trying to separate a chemical or product from a mixture
When heating under reflux, you aim to keep all the chemicals inside the reaction vessel
Example reactions where heating under reflux could be used include:
The production of a carboxylic acid from a primary alcohol using acidified potassium dichromate
The production of an ester from an alcohol and acid in the presence of an acid catalyst
The reaction mixture is placed into a pear-shaped or round-bottomed flask
Anti-bumping granules are added to promote smooth boiling
The flask is placed in a heating mantle or it can be immersed in a water bath for heating
Quickfit apparatus is then set up with the condenser clamped vertically in place
The joints of the Quickfit apparatus are commonly greased as with distillation
A steady and constant stream of water passes through the condenser in a 'water jacket' - it enters at the bottom of the condenser and the drainage pipe removes the water from the top of the condenser
The flask is indirectly heated and the reaction mixture is allowed to boil
Finally, heating stops and the mixture is allowed to cool back to room temperature
Heating under reflux practical equipment
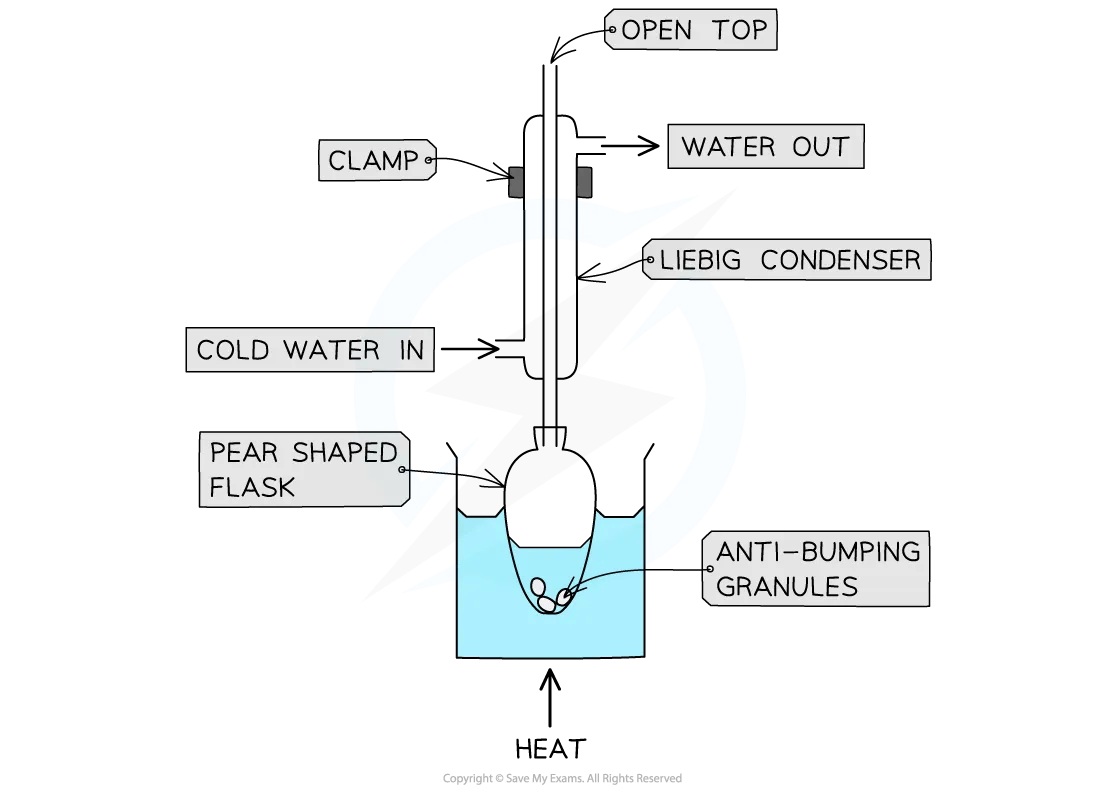
The preparation of ethyl ethanoate involves heating under reflux for about 15 minutes
Colorimetry / spectrophotometry
Colorimetry and spectrophotometry are techniques used to measure the concentration of substances in a solution based on the absorbance / transmittance of light at specific wavelengths
Both techniques use the same basic method:
A light source emits a beam of light covering a wide range of wavelengths
The sample solution absorbs certain wavelengths of light, depending on its composition and concentration
The absorbance and transmittance of various wavelengths are then recorded
The detector on a colorimeter measures the intensity of light which is directly related to the concentration of the solution
It is a relatively quick process although not as precise as spectrophotometry, especially with low concentrations or complex mixtures
The detector on a spectrophotometer measures the absorbance of each wavelength of light
The resulting absorption spectrum is plotted, showing the characteristic absorption peaks of the sample
The concentration is then determined by comparing this spectrum to a calibration curve
Spectrophotometry is highly sensitive and accurate, making it suitable for analysing low concentrations and complex mixtures
It is widely used in research, quality control, drug analysis, environmental monitoring and food testing
For more information about calorimetry, see our revision note on Measuring Rates of Reaction
Physical and digital molecular modelling
Physical molecular modelling is the creation of three-dimensional models using materials such as plastic balls and sticks (molymods)
It serves as a tool to understand molecular geometry, bond angles and the overall spatial arrangement of atoms within a molecule
Digital molecular modelling uses specialist computer software to generate accurate and detailed 3D models of molecules
By giving specific data, such as bond lengths and angles, the software can produce highly accurate representations of molecules, including their electronic structures
It allows the study of more complex molecules, especially ones that are challenging to construct
It allows observations of molecular movements and reactions in real time
Digital molecular modelling provides access to various tools and simulations that can predict:
Molecular properties
Behaviour in different environments
Potential interactions with other molecules
These simulations aid researchers in drug design, material science and many other applications

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?



