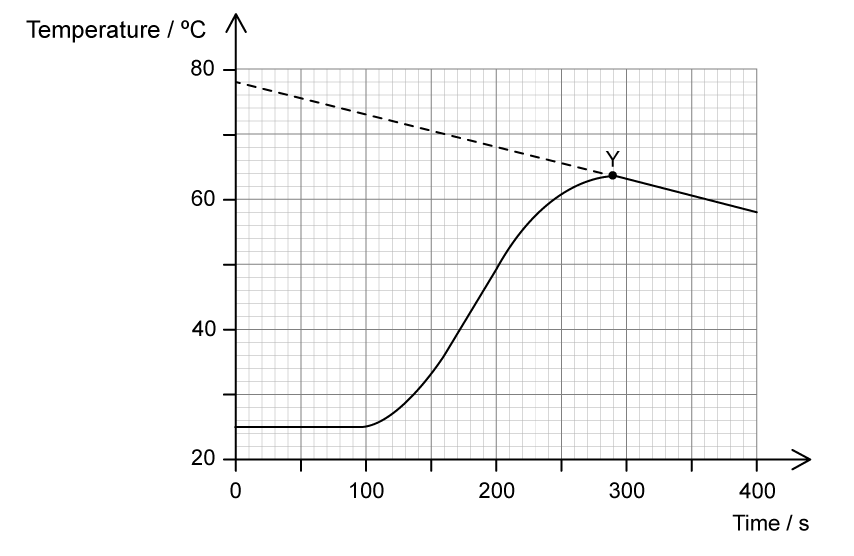
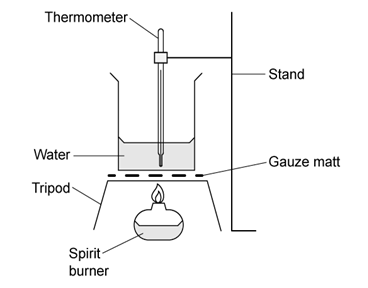
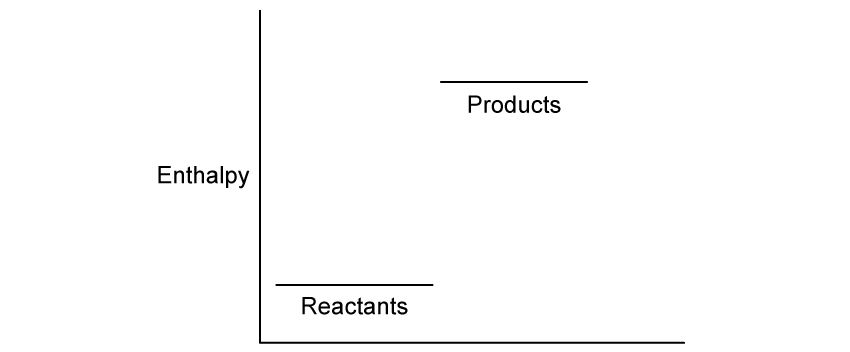
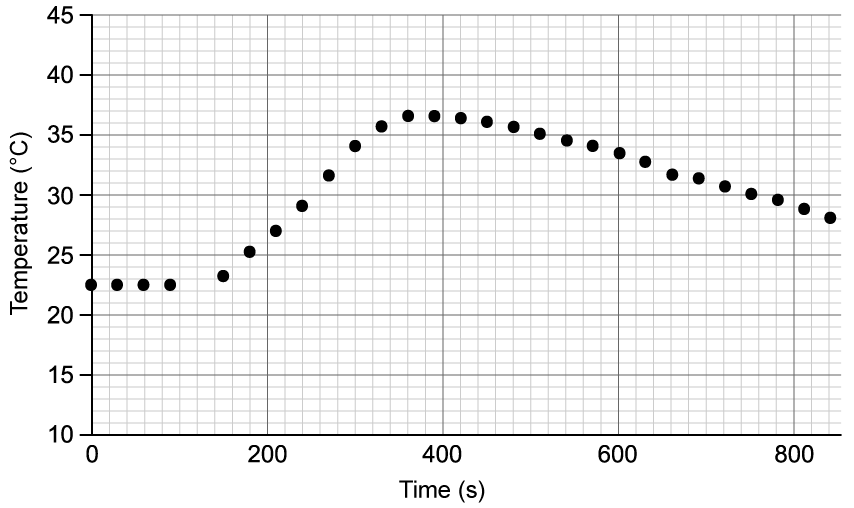
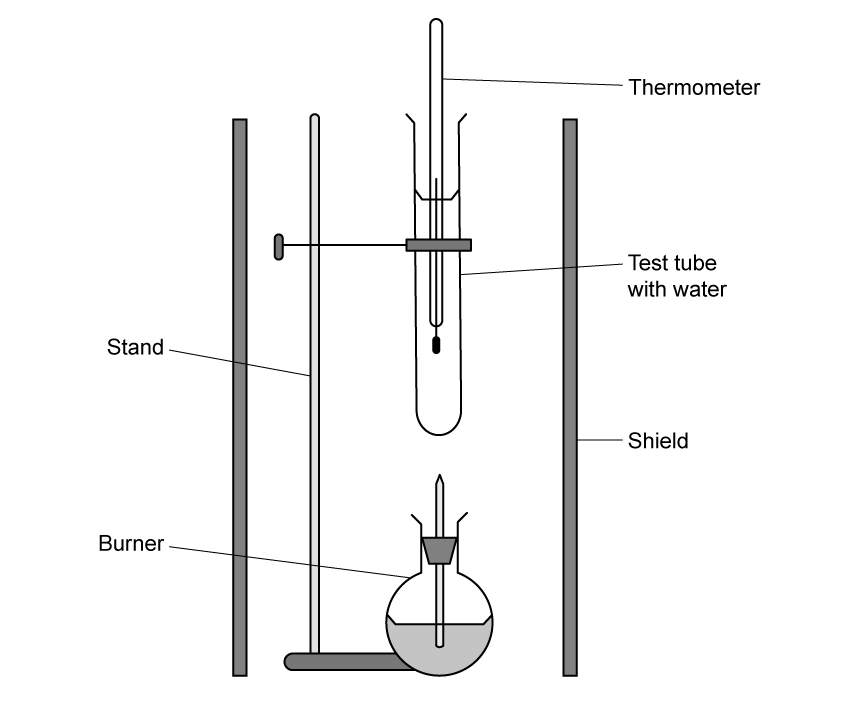
Chemical reactions can be exothermic or endothermic. State which type of reaction is indicated by a decrease in temperature.
State the type of reaction in which the energy of the system decreases.
The reaction of propane with oxygen is represented by the following equation
C3H8 + 5O2 → 3CO2 + 4H2O ΔH = -2219 kJ mol-1
State the classification of the enthalpy change is occurring in this reaction.
Define the term enthalpy of formation, ΔHf , and state the standard conditions.
Did this page help you?