The Ion Product of Water (DP IB Chemistry): Revision Note

The ion product of water

pH of water

• An equilibrium exists in water, where a few water molecules dissociate into proton and hydroxide ions

H₂O (l) ⇌ H⁺ (aq) + OH^– (aq)

• The equilibrium constant for this reaction is:

K_c x [H₂O] = [H⁺][OH^–]

• Since the concentration of the H⁺ and OH^- ions is very small, the concentration of water is considered to be a constant

• This means that the expression can be rewritten as:

K_w = [H⁺] [OH^-]

• Where K_w (ion product of water) =  K_c x [H₂O] =  1.00 10^-14 at 298K

• The product of the two ion concentrations is always 1.00 x 10^–14 

• This makes it straightforward to see the relationship between the two concentrations and the nature of the solution:

[H⁺] & [OH^–] Table

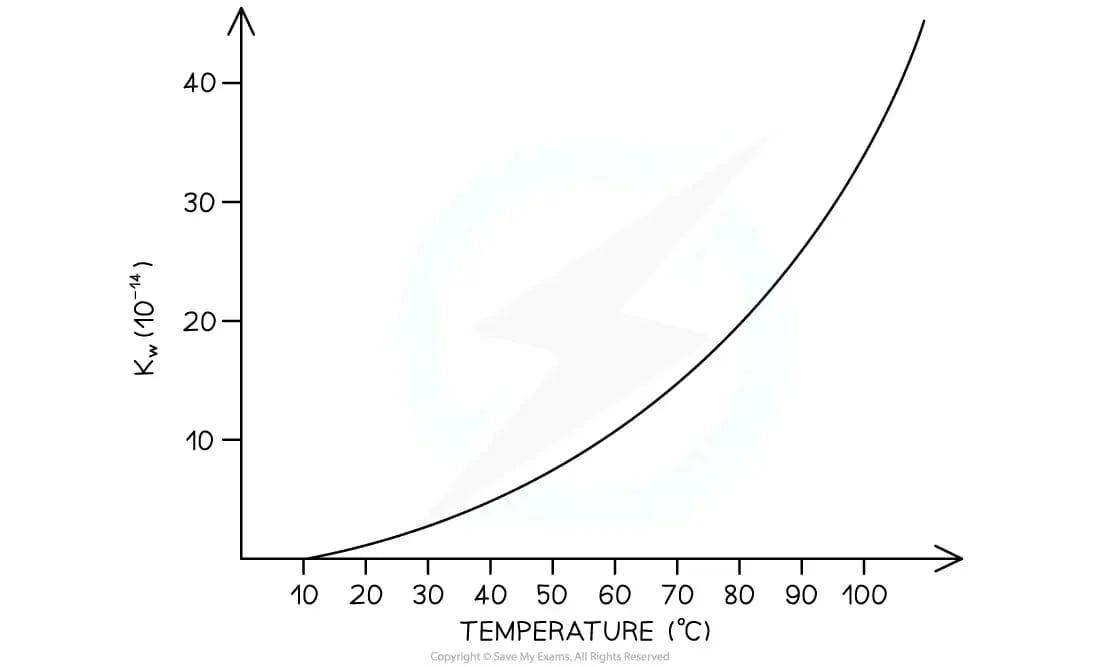
How does temperature affect the ion product of water, K_w?

• The ionisation of water is an endothermic process

2H₂O (l) ⇌ H₃O⁺  (aq) + OH^- (aq) 

• According to Le Châtelier's principle, if the temperature is increased, the equilibrium will shift to the right to absorb the added heat

  • This causes the concentrations of both H⁺ and OH^- ions to increase

  • As a result, the values of K_w increases

The effect on pH

• Since the concentration of H⁺ ions has increased, the pH of the water must decrease

pH = -log₁₀[H⁺]

• Due to the negative sign in the formula, as [H⁺] increases, pH decreases

  • Increasing the temperature decreases the pH of water (becomes more acidic)

  • Decreasing the temperature increases the pH of water (becomes more basic)

Graph to show how K_w changes with temperature