The Ion Product of Water (DP IB Chemistry)

The Ion Product of Water

pH of water

• An equilibrium exists in water, where a few water molecules dissociate into proton and hydroxide ions

H₂O (l) ⇌ H⁺ (aq) + OH^– (aq)

• The equilibrium constant for this reaction is:

K_c x [H₂O] = [H⁺][OH^–]

• Since the concentration of the H⁺ and OH^- ions is very small, the concentration of water is considered to be a constant

• This means that the expression can be rewritten as:

K_w = [H⁺] [OH^-]

• Where K_w (ion product of water) =  K_c x [H₂O] =  1.00 10^-14 at 298K

• The product of the two ion concentrations is always 1.00 x 10^–14 

• This makes it straightforward to see the relationship between the two concentrations and the nature of the solution:

[H⁺] & [OH^–] Table

How does temperature affect the ion product of water, K_w?

• The ionisation of water is an endothermic process

2H₂O (l) ⇌ H₃O⁺  (aq) + OH^- (aq) 

• In accordance with Le Châtelier's principle, an increase in temperature will result in the forward reaction being favoured

  • This causes an increase in the concentration of the hydrogen and hydroxide ions

  • This leads to the magnitude of K_w increasing

  • Therefore, the pH will decrease

• Increasing the temperature decreases the pH of water (becomes more acidic)

• Decreasing the temperature increases the pH of water (becomes more basic)

Graph to show how K_w changes with temperature

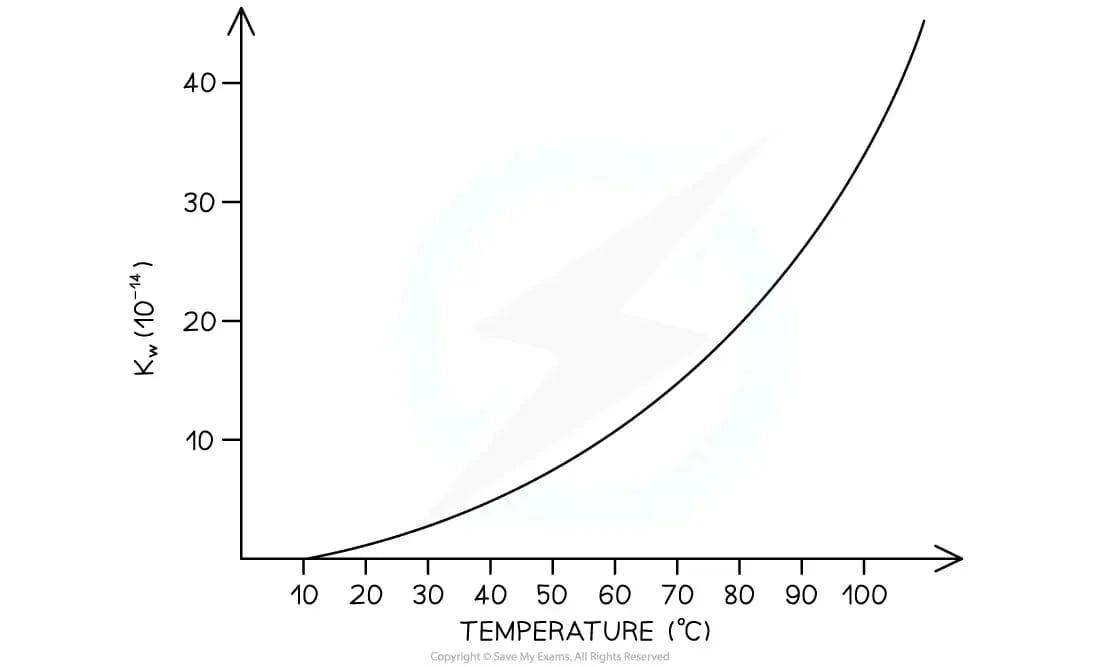
As temperature increases, K_w increases so pH decreases