Spontaneous Reactions (HL) (DP IB Chemistry) : Revision Note
Spontaneous Reactions
Gibbs free energy provides an effective way of focusing on a reaction system at constant temperature and pressure to determine its spontaneity
For a reaction to be spontaneous, Gibbs free energy must have a negative value (ΔGꝋ ≤ 0)
We can use the Gibbs equation to calculate whether a reaction is spontaneous / feasible or not
ΔGꝋ = ΔHreactionꝋ – TΔSsystemꝋ
When ΔGꝋ is negative, the reaction is spontaneous / feasible and likely to occur
When ΔGꝋ is positive, the reaction is not spontaneous / feasible and unlikely to occur
Depending on the value for ΔH and ΔS we can determine whether the reaction is spontaneous at a given temperature (T)
We can also look at the values for enthalpy change, ΔH, and entropy change, ΔS
Worked Example
Determining if a reaction is feasible / spontaneous
Calculate the Gibbs free energy change for the following reaction at 298 K
Determine whether the reaction is feasible.
2Ca (s) + O2 (g) → 2CaO (s) ΔH = -635.5 kJ mol-1
Sꝋ[Ca(s)] = 41.00 J K-1 mol-1
Sꝋ[O2(g)] = 205.0 J K-1 mol-1
Sꝋ[CaO(s)] = 40.00 J K-1 mol-1
Answer 1:
Step1: Calculate ΔSsystemꝋ
ΔSsystemꝋ = ΣΔSproductsꝋ – ΣΔSreactantsꝋ
ΔSsystemꝋ = (2 x ΔSꝋ [CaO(s)]) – (2 x ΔSꝋ [Ca(s)] + ΔSꝋ [O2(g)])
= (2 x 40.00) – (2 x 41.00 + 205.0)
= -207.0 J K-1 mol-1
Step 2: Convert ΔSꝋ to kJ K-1 mol-1
ΔSsystemꝋ =
-0.207 kJ mol-1
Step 3: Calculate ΔGꝋ
ΔGꝋ = ΔHreactionꝋ – TΔSsystemꝋ
ΔGꝋ = -635.5 – (298 x -0.207)
= –573.8 kJ mol-1
Answer 2:
Since ΔGꝋ is negative, the reaction is feasible
Factors affecting ΔG and the spontaneity / feasibility of a reaction
We can also look at the values for ΔH and ΔS to determine whether the reaction is spontaneous / feasible at a given temperature (T)
The Gibbs equation will be used to explain what will affect the spontaneity / feasibility of a reaction for exothermic and endothermic reactions
Gibbs free energy equation

Exothermic reactions
In exothermic reactions, ΔHreactionꝋ is negative
If the ΔSsystemꝋ is positive:
Both the first and second terms will be negative
Resulting in a negative ΔGꝋ so the reaction is feasible
Therefore, regardless of the temperature, an exothermic reaction with a positive ΔSsystemꝋ will always be feasible
If the ΔSsystemꝋ is negative:
The first term is negative and the second term is positive
At very high temperatures, the –TΔSsystemꝋ will be very large and positive and will overcome ΔHreactionꝋ
Therefore, at high temperatures ΔGꝋ is positive and the reaction is not feasible
Since the relative size of an entropy change is much smaller than an enthalpy change, it is unlikely that TΔS > ΔH as temperature increases
These reactions are therefore usually spontaneous under normal conditions
Flow chart to determine the feasibility of exothermic reactions
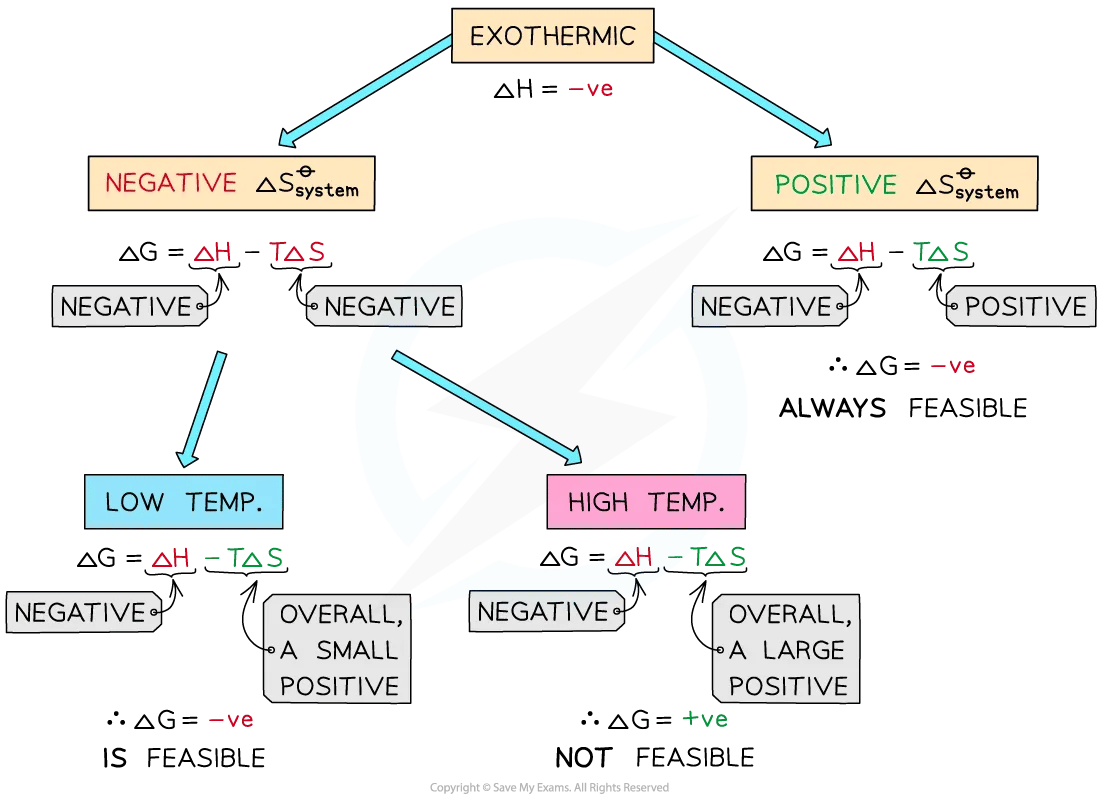
The diagram shows under which conditions exothermic reactions are feasible
Endothermic reactions
In endothermic reactions, ΔHreactionꝋ is positive
If the ΔSsystemꝋ is negative:
Both the first and second term will be positive
Resulting in a positive ΔGꝋ so the reaction is not feasible
Therefore, regardless of the temperature, endothermic with a negative ΔSsystemꝋ will never be feasible
If the ΔSsystemꝋ is positive:
The first term is positive and the second term is negative
At low temperatures, the –TΔSsystemꝋ will be small and negative and will not overcome the larger ΔHreactionꝋ
Therefore, at low temperatures ΔGꝋ is positive and the reaction is not feasible
The reaction is more feasible at high temperatures as the second term will become negative enough to overcome the ΔHreactionꝋ resulting in a negative ΔGꝋ
This tells us that for certain reactions which are not feasible at room temperature, they can become feasible at higher temperatures
An example of this is found in metal extractions, such as the extraction if iron in the blast furnace, which will be unsuccessful at low temperatures but can occur at higher temperatures (~1500 oC in the case of iron)
Flow chart to determine the feasibility of endothermic reactions
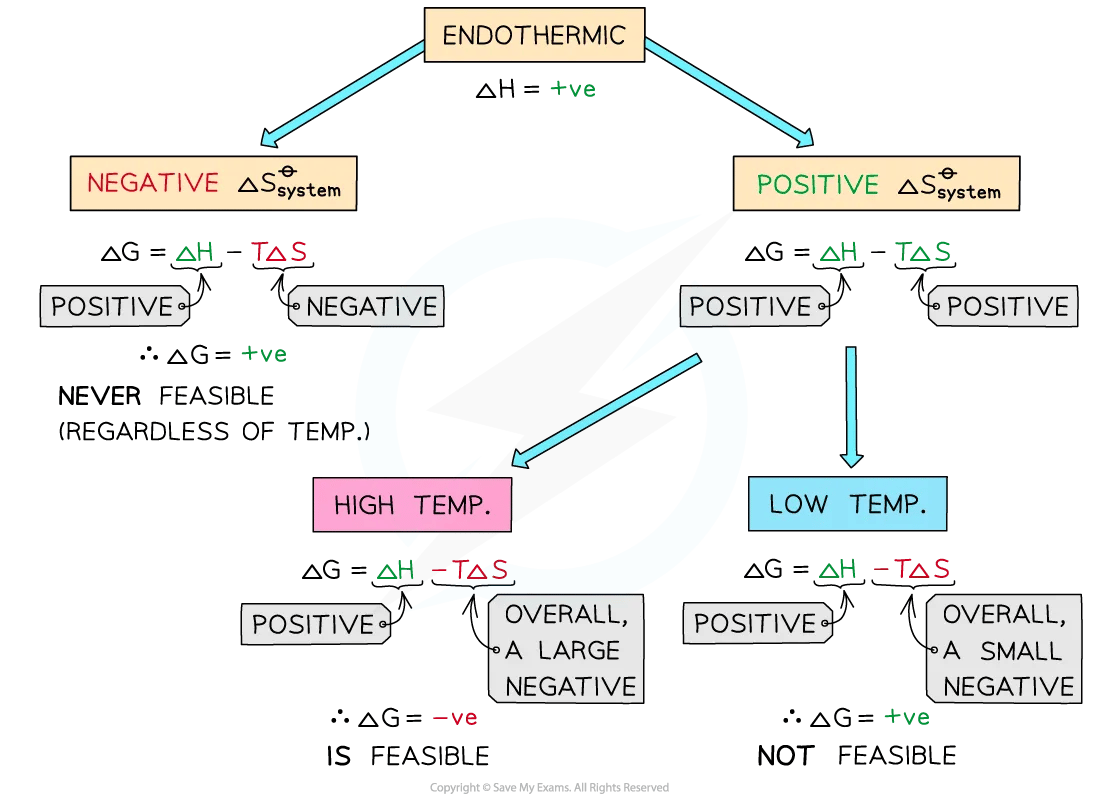
The diagram shows under which conditions endothermic reactions are feasible
Summary of factors affecting Gibbs free energy
If ΔH .... | And if ΔS .... | Then ΔG is | Spontaneous? | Because |
|---|---|---|---|---|
is negative < 0 exothermic | is positive > 0 more disorder | always negative < 0 | Always | Forward reaction spontaneous at any T |
is positive > 0 endothermic | is negative < 0 more order | always positive > 0 | Never | Reverse reaction spontaneous at any T |
is negative < 0 exothermic | is negative < 0 more order | negative at low T positive high T | Dependent on T | Spontaneous only at low T TΔS < H |
is positive > 0 endothermic | is positive > 0 more disorder | negative at high T positive low T | Dependent on T | Spontaneous only at high T TΔS > H |
Temperature & Spontaneity
Rearranging the Gibbs equation allows you to determine the temperature at which a non-spontaneous reaction become feasible
ΔGꝋ = ΔHreactionꝋ - TΔSsystemꝋ
Remember, for a reaction to be feasible ΔGΘꝋmust be zero or negative
0 = ΔHꝋ - TΔSꝋ
ΔHꝋ = TΔSꝋ
T =
Worked Example
At what temperature will the reduction of aluminium oxide with carbon become spontaneous?
Al2O3 (s) + 3C (s)→ 2Al (s) + 3CO (g)
ΔHꝋ = +1336 kJ mol-1
ΔSꝋ = +581 J K-1 mol-1
Answer:
If ΔGꝋ = 0 then T =
Covert ΔSꝋ to kJ K-1 mol-1 by dividing by 1000
T =
= 2299 K

You've read 1 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?

