Molar Gas Volume (DP IB Chemistry)

Molar Gas Volume

• Gases in a container exert a pressure as the gas molecules are constantly colliding with the walls of the container

A particle model of a gas in a container

Gas particles exert a pressure by constantly colliding with the walls of the container

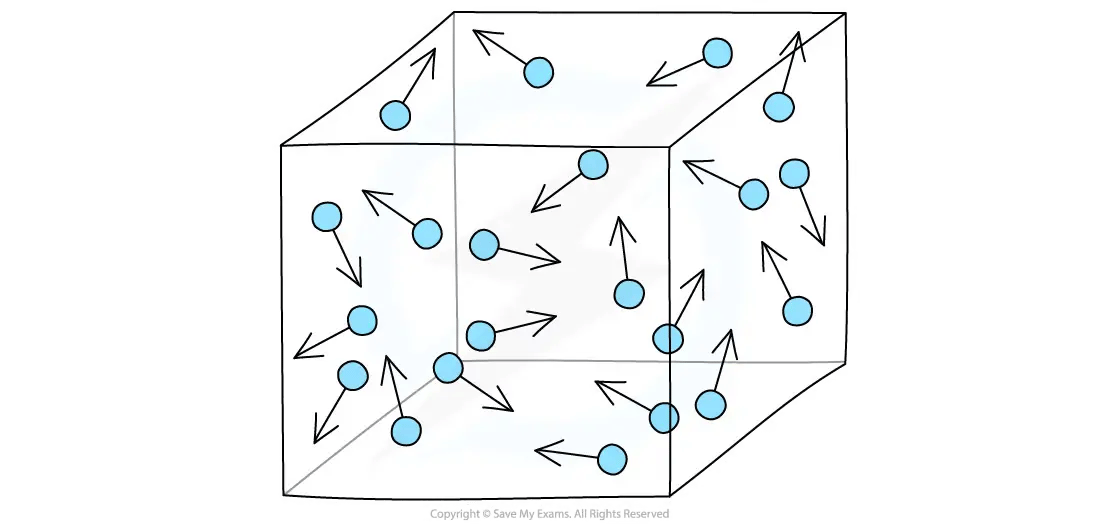
Changing gas volume

• Decreasing the volume (at constant temperature) of the container causes the molecules to be squashed together which results in more frequent collisions with the container wall

• The pressure of the gas increases

Gas Molecule Collision Frequency with Increasing Pressure Diagram

Decreasing the volume of a gas causes an increased collision frequency of the gas particles with the container wall

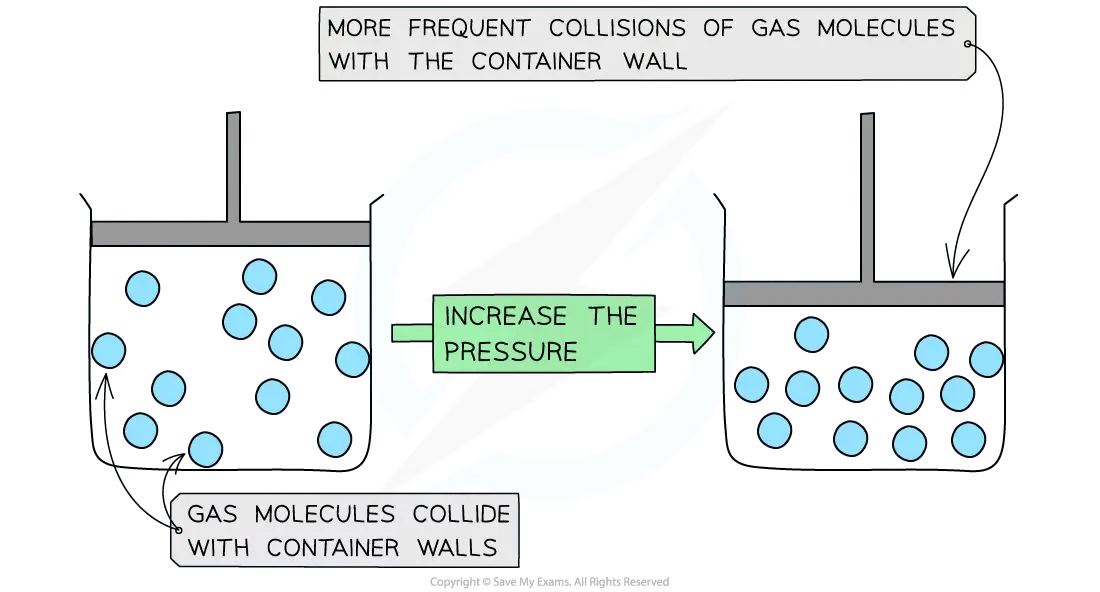
• The pressure is therefore inversely proportional to the volume (at constant temperature)

• This is known as Boyle's Law

• Mathematically, we say P ∝ 1 / V or PV = a constant

• We can show a graphical representation of Boyle's Law in three different ways:

  • A graph of pressure of gas plotted against 1 / volume gives a straight line

  • A graph of pressure against volume gives a curve

  • A graph of PV versus P gives a straight line

Sketch graphs of Boyles' Law

Three graphs that show Boyle’s Law

Changing gas temperature

• When a gas is heated (at constant pressure) the particles gain more kinetic energy and undergo more frequent collisions with the container walls

• To keep the pressure constant, the molecules must get further apart and therefore the volume increases

• The volume is therefore directly proportional to the temperature in Kelvin (at constant pressure)

• This is known as Charles' Law

• Mathematically, V ∝ T or V / T = a constant

• A graph of volume against temperature in Kelvin gives a straight line

Gas Molecule Collision Frequency with Increasing Temperature Diagram

Increasing the temperature of a gas causes an increased collision frequency of the gas particles with the container wall (a); volume is directly proportional to the temperature in Kelvin (b)

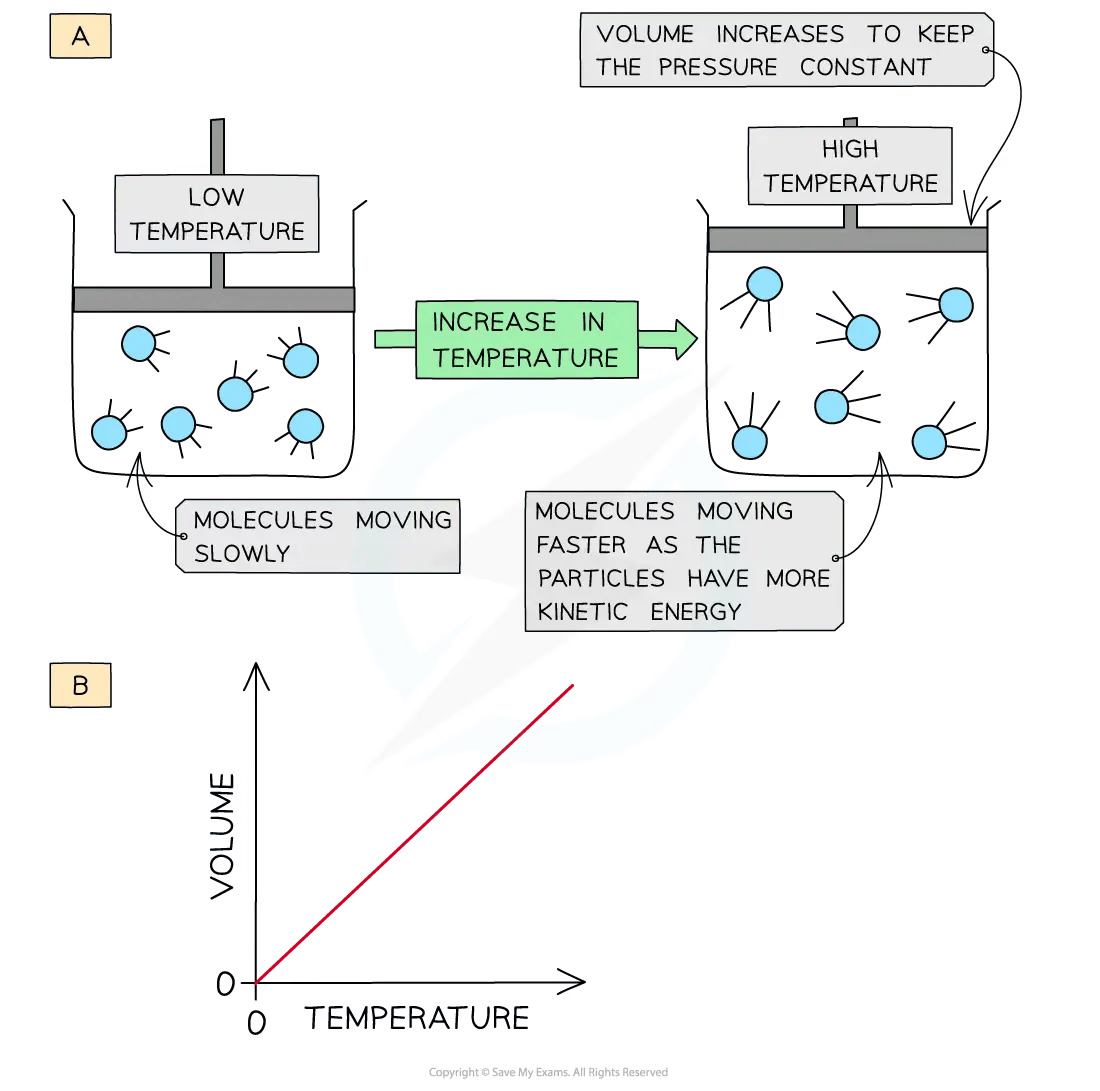
Changing gas pressure

• Increasing the temperature (at constant volume) of the gas causes the molecules to gain more kinetic energy

• This means that the particles will move faster and collide with the container walls more frequently

• The pressure of the gas increases

• The temperature is therefore directly proportional to the pressure (at constant volume)

• Mathematically, we say that P ∝ T or P / T = a constant 

• A graph of temperature in Kelvin of a gas plotted against pressure gives a straight line

Gas Molecule Collision Frequency with Increasing Pressure at Constant Volume Diagram

Increasing the temperature of a gas causes an increased collision frequency of the gas particles with the container wall (a); temperature is directly proportional to the pressure (b)

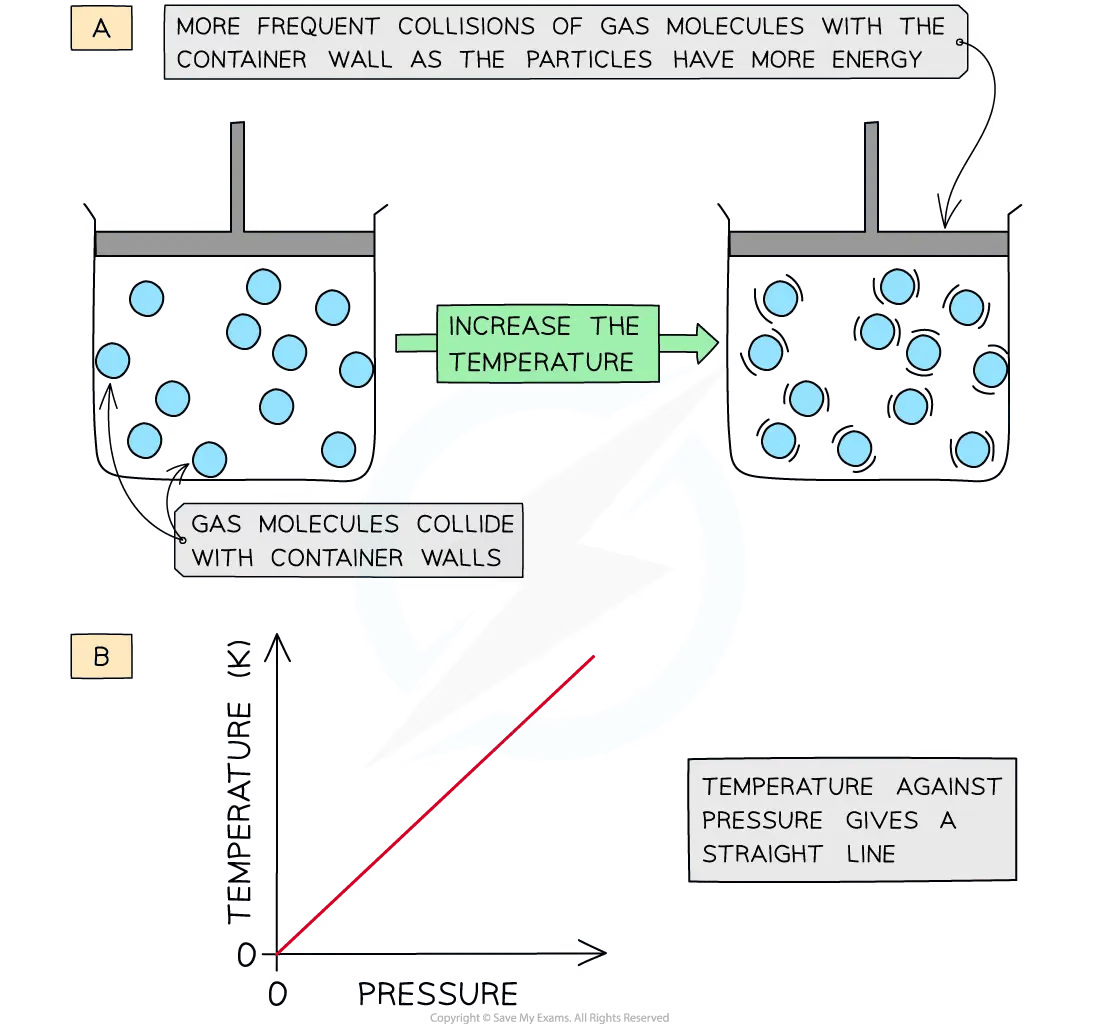
Pressure, volume and temperature

• Combining these three relationships together:

  • PV = a constant

  • V / T = a constant

  • P / T = a constant

• We can see how the ideal gas equation is constructed

  • PV / T = a constant

  • PV = a constant x T

• This constant is made from two components, the number of moles, n, and the gas constant, R, resulting in the overall equation:

  • PV = nRT

Changing the conditions of a fixed amount of gas

• For a fixed amount of gas, n and R will be constant, so if you change the conditions of a gas we can ignore n and R in the ideal gas equation

• This leads to a very useful expression for problem solving

• Where P₁, V₁ and T₁ are the initial conditions of the gas and P₂, V₂ and T₂ are the final conditions