Descriptive Statistics (DP IB Business Management)

RapidKleen kept a record of mobile vehicle valets carried out each day during a busy holiday period.

Find the mean, median, mode, and range of mobile valets during the period using the following data:

[6 marks]

Answer:

Step 1: To calculate the mean, first add together each of the values

14 + 10 + 12 + 12 + 14 + 15 + 14 = 91

Step 2: Divide the total by the number of values

91 ÷ 7 = 13 [2 marks]

• Note that the mean in this case isn't a value from the original data set

• This is a common result - you should not assume that your mean will be one of your original numbers and you should not be surprised when it isn't

Step 3: To calculate the median first rewrite the data set in numerical order

10, 12, 12, 14, 14, 14, 15

Step 4: Identify the middle number

• There are seven numbers in the list, so the middle one will be the (7 + 1) ÷ 2 = 8 ÷ 2 = 4th number:

10, 12, 12, 14, 14, 14, 15

So the median is 14 [2 marks]

• Note: The formula for the place to find the median is "([the number of data points] + 1) ÷ 2", but you don't have to use this formula

  • You can just count in from both ends of the list until you meet in the middle if you prefer, especially if the data set is small
    

Step 5: To calculate the mode rewrite the data set in numerical order

10, 12, 12, 14, 14, 14, 15

Step 6: Identify the number that occurs most often in the list

14 occurs three times

14 occurs x3

12 appears x2

10 appears x1

15 appears x1

As it appears most frequently, the mode number of valets sold is 14 [2 marks]

FreshBite is a pre-packaged sandwich manufacturer which produces a range of products that are sold in cafés and refreshment stands in tourist attractions such as theme parks.

Freshbite's sales are highly variable - the business regularly suffers from high levels of wastage as a result of having large quantities of unsold stock. On several occasions it has also been unable to fulfil orders from customers as it has not produced enough units.

The business has recently employed a new operations manager who has suggested that calculating the standard deviation of sales would aid planning. He has requested the last month's sales data to allow him to calculate this.

Calculate the standard deviation of last months' sales for Freshbite. 

[4 marks]

Answer:

Step 1: Calculate the mean

110,000 + 27,000 + 12,000 + 54,000 + 6,000 = 210,000

210,000 ÷ 5 = 42,000 [1 mark]

Step 2: For each product, subtract the mean and square the result

[1 mark]

Step 3: Add up the squared differences and express in an expanded form

4,624 + 225 + 900 + 144 + 1,225 = 7,118

= 7,118,000 [1 mark]

Step 4: Find the square root to identify the standard deviation 

[1 mark]

Note - in this instance, a significant standard deviation from the mean informs Freshbite's managers that they need to carefully plan for significant variations in sales. This may include detailed market research as well as capital investment to reduce wastage (for example, further freezers).

BestGrip is shoe manufacturing business that employs a team of sales managers who receive performance-related monthly bonuses on top of their monthly salaries.

Bonuses are awarded to those sales managers who achieve sales in the top quartile.

Sales data for the month of May are shown in the table below.

Identify the sales managers to be awarded a bonus in May.

[4 marks]

Answer:

Step 1: Put the list of data into order, from smallest to largest

[2 marks]

Step 2: Divide the list into four equal parts:

[1 mark]

Step 3: Identify the data within the top quartile

• In this case, sales managers L, H and J will receive a performance-related bonus in May [1 mark]

Maggri Spice Ltd manufactures a range of hot curry pastes that are sold online and in specialist stores.

In 2022 total sales were $180,000, with sales for individual products shown in the pie chart below.

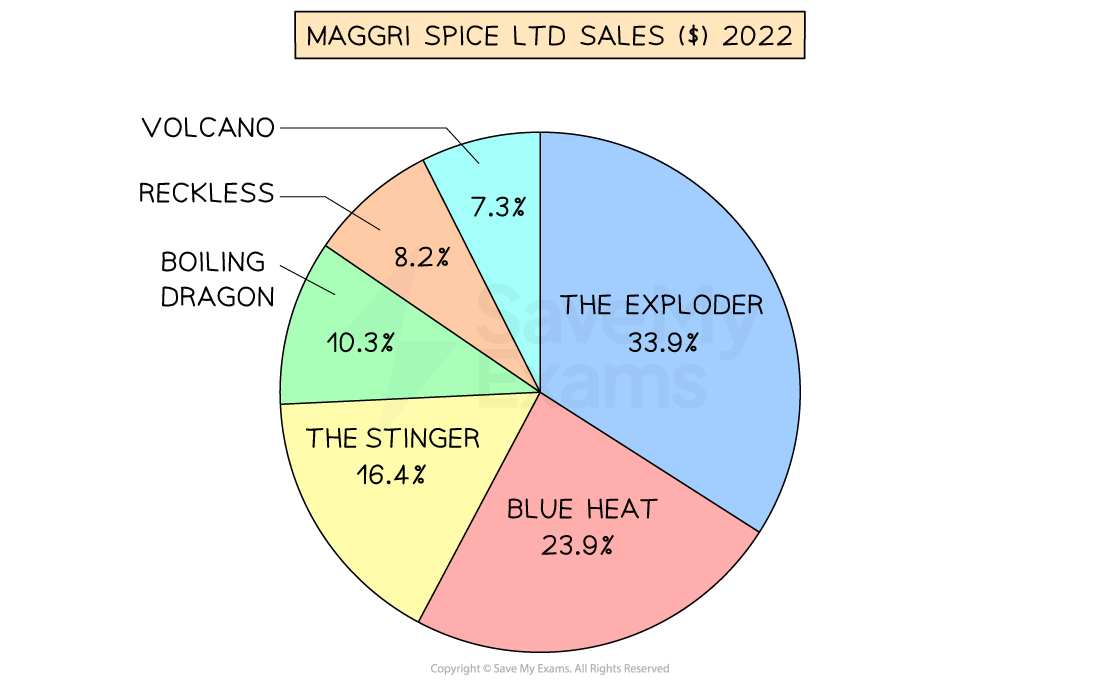
Calculate the value of sales of Blue Heat curry paste in 2022.

[2 marks]

Answer:

Step 1: Identify the percentage of total sales attributed to Blue Heat

In this case, 23.9% of total sales can be attributed to Blue Heat

Step 2: Convert the percentage to a decimal

23.9% = 0.239 [1 mark]

Step 3 - Multiply total sales by the decimal

$180,000 x 0.239 = $43,020

Blue Heat curry paste achieved sales of $43,020 in 2022 [1 mark]

You can make use of descriptive statistical techniques throughout both exam papers.

They are particularly useful when making comparisons or supporting chains of analysis to lead to a judgement. You do not have to wait to be told to use them in your work - become accustomed to applying them to data in your work as you move through the course.

Interpreting data using these tools is a higher level approach to application and demonstrates that you are making optimum use of data presented in case study materials - this really does impress the examiner!