Critical Path Analysis (DP IB Business Management): Revision Note
The nature and purpose of critical path analysis
Critical path analysis is a project management tool that uses network analysis to plan complex and time-sensitive projects
It involves the construction of a visual model of the project that includes key elements
A list of all activities required to complete the project
The time (duration) that each activity will take to complete
How each project activity depends on others
Critical Path Analysis shows
The order in which activities must be completed
The longest path of project activities to the completion of the project
The earliest and latest that each project activity can start and finish without delaying completion of the project as a whole
Activities within a project that can be carried out simultaneously are identified
The critical project activities which if delayed will cause the project as a whole to over-run
Those project activities where some delay is acceptable without delaying the project as a whole
The shortest time possible to complete the project
It allows managers to identify the relationships between the activities involved and to work out the most efficient way of completing the project
Resources such as raw materials and components can be ordered or hired at precisely the right time they are needed
Working capital may be managed efficiently
Where delays occur managers can identify the implications for the project’s completion and redirect resources if required
Components of network analysis diagrams
Example network analysis

A network diagram must always start and end on a single node
Lines must not cross and must only be assigned to activities
Elements of a network diagram
Element | Description |
|---|---|
Node |
|
Activities |
|
Duration |
|
Calculating earliest start times
Working forward from Node 1, it is possible to calculate the Earliest Start Time for each activity by adding the duration of each task
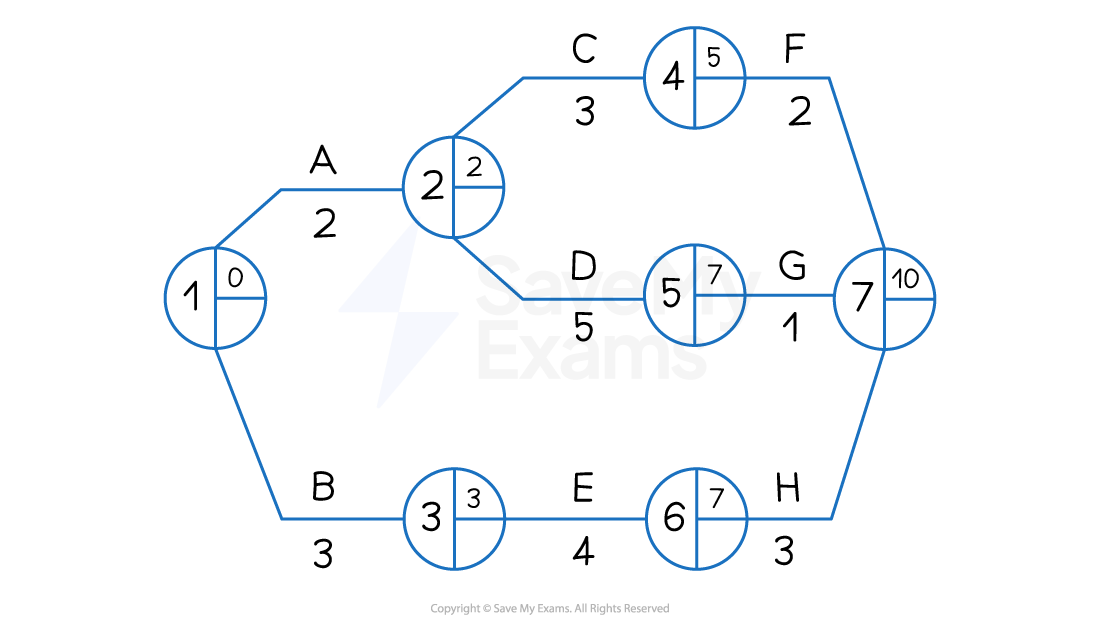
Network diagram analysis
The EST for each activity is placed in the top right of each node
Node 1 is the starting point of the project and where both Activity A and Activity B begin
Activity A and Activity B are independent processes
Activity A has a duration of 2 days and its earliest start time (EST) is 0 days
Activity B has a duration of 3 days and its EST is also 0 days
Activity C and Activity D both begin at Node 2 and are dependent upon the completion of Activity A but are independent from each other
Activity C has a duration of 3 days and its EST is 2 days
Activity D has a duration of 5 days and its EST is also 2 days
Activity E begins at Node 3
Activity E has a duration of 4 days and its EST is 3 days
Activity F begins at Node 4
Activity F has a duration of 2 days and its EST is 5 days
Activity G begins at Node 5
Activity G has a duration of 1 day and its EST is 7 days
Activity H begins at Node 6
Activity H has a duration of 3 days and its EST is 7 days
Node 7 is the end point of the project
Calculating latest finish times
Working backwards from Node 7, it is now possible to calculate the Latest Finish Time (LFT) for each activity by subtracting the duration of each task
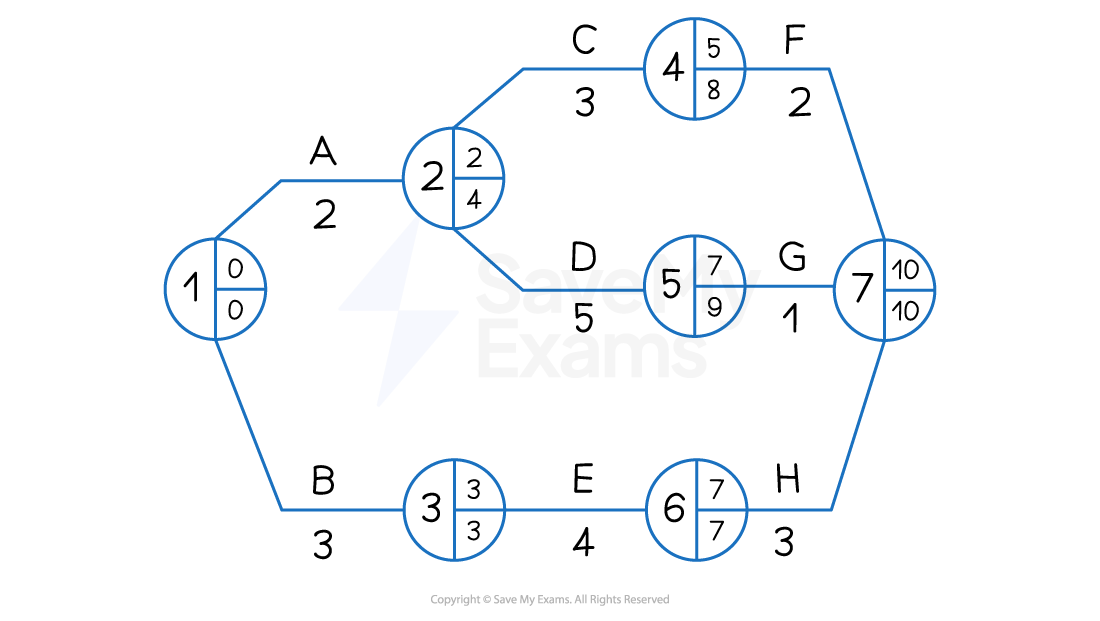
Network diagram analysis
The LFT for each activity is placed in the bottom right of each node
Node 7 is the end point of the project, which has a latest finish time of 10 days
Activity H has a duration of 3 days
The LFT in Node 6 is 7 days (10 days - 3 days)
Activity G has a duration of 1 day
The LFT in Node 5 is 9 days (10 days - 1 day)
Activity F has a duration of 2 days
The LFT in Node 4 is 8 days (10 days - 2 days)
Activity E has a duration of 4 days
The LFT in Node 3 is 3 days (7 days - 4 days)
Activity D has a duration of 5 days
The LFT in Node 2 is 4 days (9 days - 5 days)
Activity C has a duration of 3 days
The LFT in Node 3 is 4 days because Activity D is the more time-critical of the two activities that are dependent upon the completion of Activity A and so its LFT is recorded
Activity B has a duration of 3 days
The LFT in Node 1 is 0 days (3 days - 3 days)
Activity A has a duration of 2 days
The LFT in Node 1 is 0 days because Activity B is the more time-critical of the two starting activities and so its LFT is recorded
The LFT in Node 1 is always 0
Identifying the critical path
The critical path highlights those activities that determine the length of the whole project
If any of these critical activities are delayed the project as a whole will be delayed
The critical path follows the nodes where the EST and LFT are equal
In the diagram below nodes 1 3 6 and 7 have equal ESTs and LFTs
Activities that determine these nodes are B E and H
These activities are marked with two short lines
The critical path is therefore BEH
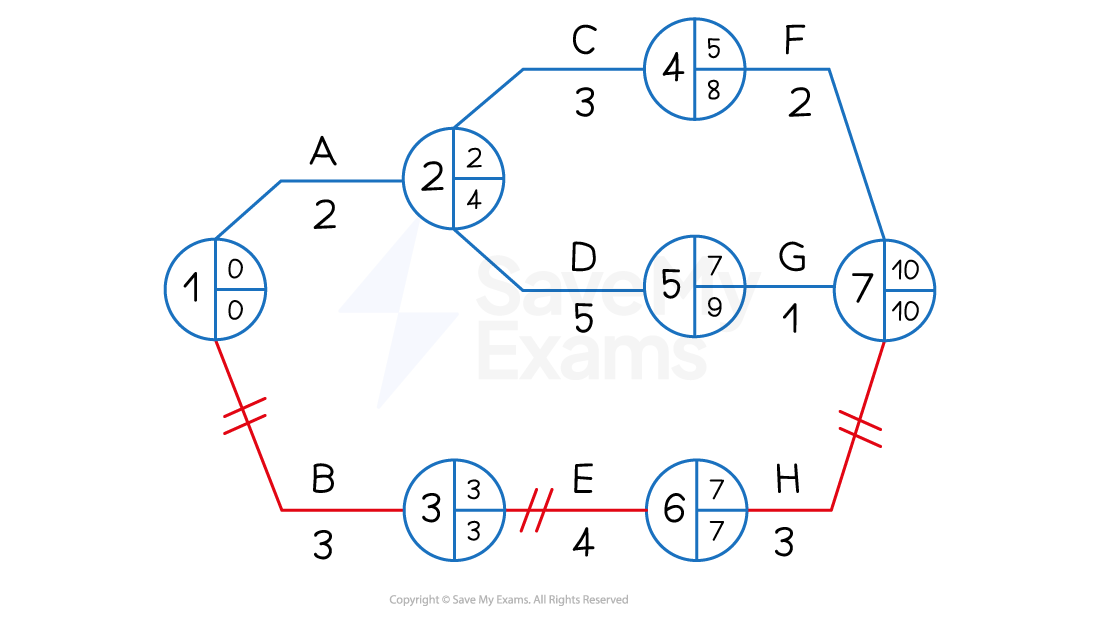
Identifying and calculating float time
Float time exists where there is a difference between the Earliest Start Time (EST and the Latest Finish Time (LFT)
Where float time is identified, managers may
Transfer resources such as staff or machinery to more critical activities
Allow extra time to complete tasks to improve quality or allow for creativity
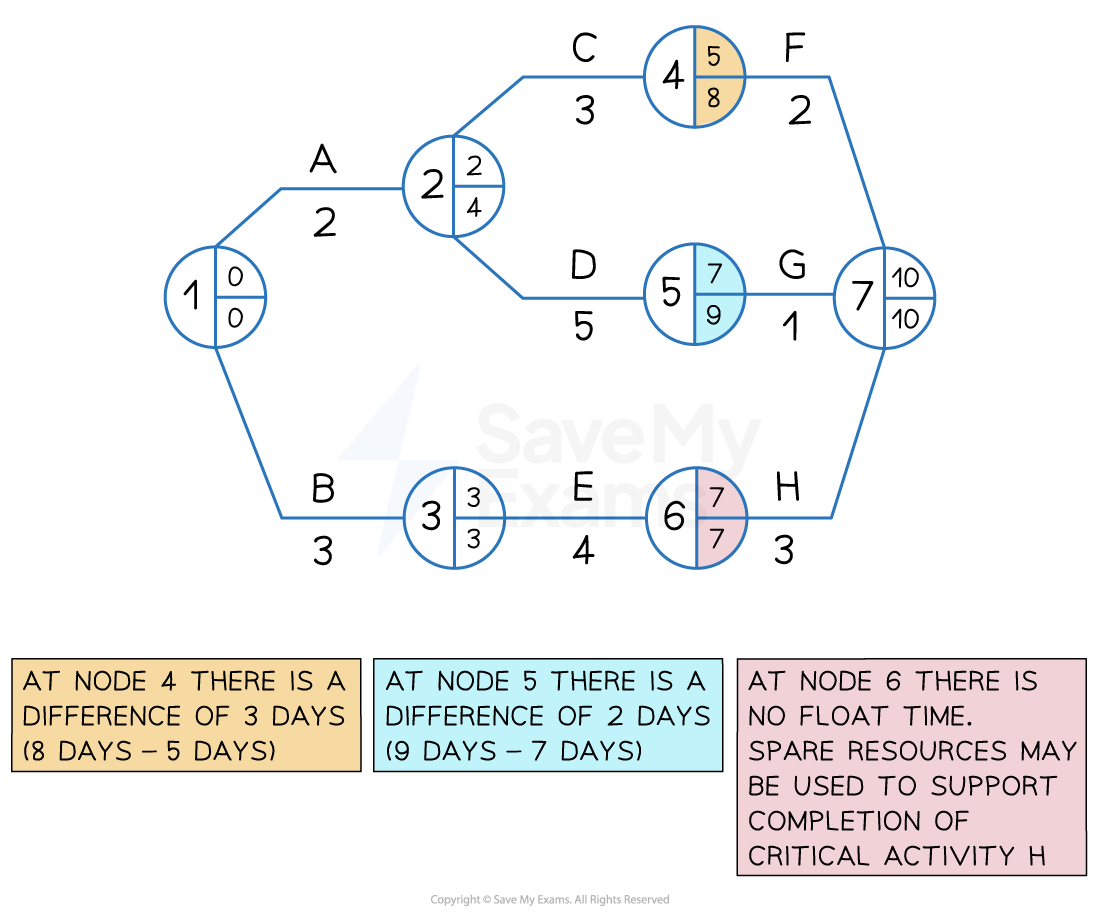
Float time analysis
The total float refers specifically to spare time that is available so that the overall project completion is not delayed
The total float for a specific activity is calculated by
LFT for the activity - Duration of the activity - EST for the activity
Using the diagram above the following total float times can be calculated for Activities A to H
Activity | LFT | - Duration | - EST | = Total Float |
|---|---|---|---|---|
A | 4 | 2 | 0 | 2 |
B | 3 | 3 | 0 | 0 |
C | 8 | 3 | 2 | 3 |
D | 9 | 5 | 2 | 2 |
E | 7 | 4 | 3 | 0 |
F | 10 | 2 | 5 | 3 |
G | 10 | 1 | 7 | 2 |
H | 10 | 3 | 7 | 0 |
The critical activities B E and H each have a total float of 0 days
Worked Example
The network diagram below shows the activities involved in a new promotional campaign for a small fashion accessories business as well as the time (in weeks) it is expected that each activity will take to complete.
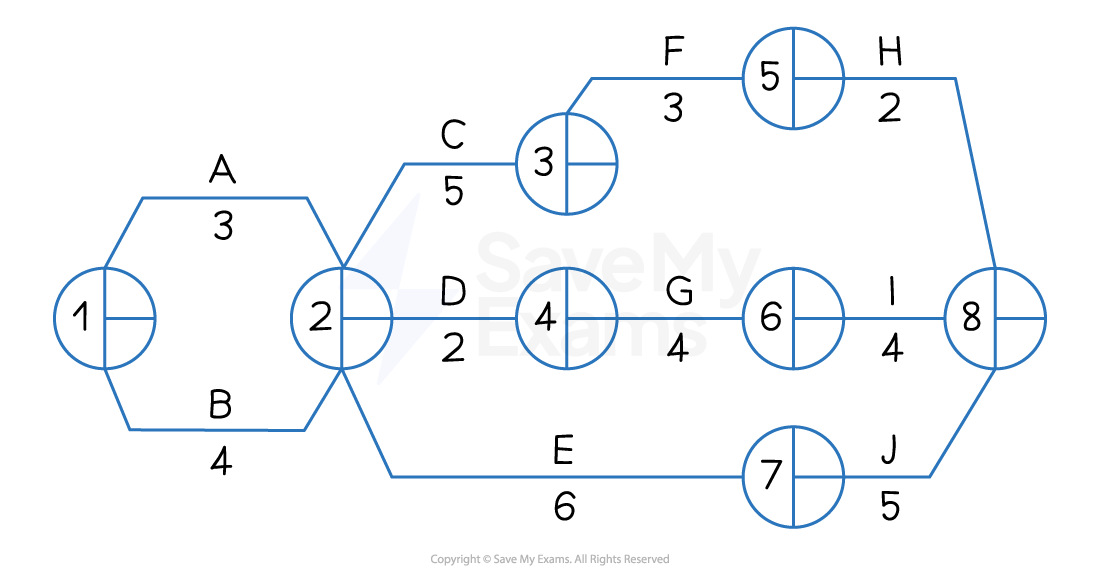
Calculate
a) The earliest start times and latest finish times for each node. (4 marks)
b) The total float time for activity G. (3 marks)
Step 1 - Calculate the Earliest Start Times (EST)
Node 1 EST = 0
Node 2 EST = 0 + 3 = 3 but 0 + 4 = 4 so 4
Node 3 EST = 4 + 5 = 9
Node 4 EST = 4 + 2 = 6
Node 5 EST = 9 + 3 = 12
Node 6 EST = 6 + 4 = 10
Node 7 EST = 4 + 6 = 10
Node 8 EST = 12 + 2 = 14 but 10 + 4 = 14 and 10 + 5 = 15 so 15
Step 2 - Calculate the Latest Finish Times (LFT)
Node 8 = 15
Node 7 = 15 - 5 = 10
Node 6 = 15 - 4 = 11
Node 5 =15 - 2 = 13
Node 4 =11 - 4 = 7
Node 3 =13 - 3 = 10
Node 2 = 10 - 6 = 4
Node 1 = 4 - 4 = 0
Step 3 - Calculate the total float time for Activity G
Total float = LFT for the activity - Duration of the activity - EST for the activity
= 11 weeks - 4 weeks - 6 weeks
= 1 week
Evaluating critical path analysis
Although Critical Path Analysis can be useful in project planning, the method has some limitations
Limitations of critical path analysis as a project planning tool
Limitations | Explanation |
|---|---|
|
|
|
|
|
|
|
|

Unlock more, it's free!
Did this page help you?