Processing Uncertainties in Biology (DP IB Biology)

Processing Uncertainties in Biology

What is uncertainty?

• Scientific measurements are not perfect; there is always an associated level of uncertainty

• Uncertainty is a quantitative indication of the quality of numerical results; it can be defined as:

The range of values around a measurement within which the true value is expected to lie

• Uncertainties in measurements are recorded as a range (±) to an appropriate level of precision, e.g.

  • If a balance that measures mass shows scale graduations of 10 g, then mass is measured to the nearest 10 g (this is known as the margin of error)

    • The true value could be 5 g higher or lower than the measured value, so the uncertainty would be ±5 g

  • If a pipette shows scale graduations every 0.1 cm³, then volume is measured to the nearest 0.1 cm³

    • The true value could be 0.05 cm³ more or less than this, so the uncertainty would be ±0.05 cm³

• Note that uncertainty is not the same as error

  • Error is the difference between a measured value and the true value for a measurement

  • Errors arise from equipment or practical techniques that cause a reading to be different from the true value

Error bars

• The uncertainty in a measurement can be shown on a graph as an error bar

  • This bar is drawn above and below the point (or from side to side) and shows the uncertainty in that measurement

  • Usually, error bars will be in the vertical direction, for y-values, but can also be plotted horizontally, for x-values

• Range, degree of precision, standard error and standard deviation can be expressed on a graph using error bars

  • Range = the difference between the lowest and highest value

  • Degree of precision = how close a set of data points are to each other

  • Standard error = an estimate of the reliability of the mean

  • Standard deviation = the spread of data around the mean

• Note that it is important that you know what is represented by error bars on a graph, e.g. whether they represent standard deviation or standard error; in an exam this information would be provided in the question

  • Error bars that represent standard deviation can be used to assess whether or not two data sets are significantly different to each other

  • Overlapping error bars indicate that two sets of data are not significantly different

• Error bars are used in the specification when measuring osmotic concentration

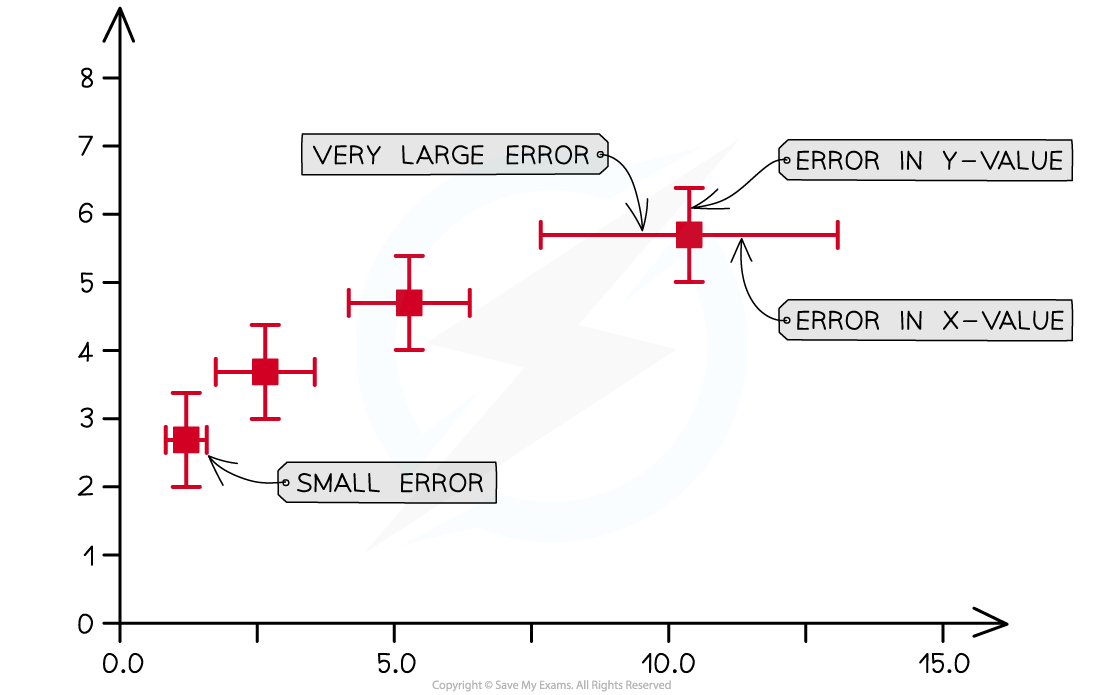
Error bars on a graph can be used to show uncertainty

Level of precision

• Measurements and processed uncertainties must be expressed to an appropriate level of precision

  • E.g. number of decimal places

• This may depend on the sensitivity of the apparatus used to collect data; the level of precision used to express the data should not exceed the level of precision at which the data is initially measured

• Values in a raw data set should all be expressed to the same level of precision

The coefficient of determination, R²

• The coefficient of determination is a measure of fit that can be applied to lines and curves on graphs

• The coefficient of determination is written as R² 

• It is used to evaluate the fit of a trend line / curve with its data set:

  • R² = 0

    • The dependent variable cannot be predicted from the independent variable. 

    • R² is usually greater than or equal to zero

  • R² between 0 and 1

    • The dependent variable can be predicted from the independent variable, although the degree of success depends on the value of R² 

    • The closer to 1, the better the fit of the trend line / curve

  • R² = 1

    • The dependent variable can be predicted from the independent variable

    • The trend line / curve is a perfect fit  

    • Note: This does not guarantee that the trend line / curve is a good model for the relationship between the dependent and independent variables

• Coefficient of determination is used in the specification when comparing the speed of nerve impulse transmission

Correlation

• Correlation is an association, or relationship, between variables

  • Note that there is a clear distinction between correlation and causation: correlation does not necessarily indicate a causal relationship

  • Causation occurs when one variable has an influence or is influenced by another

• Correlation can be positive or negative

  • Positive correlation: as variable A increases, variable B increases

  • Negative correlation: as variable A increases, variable B decreases

• The correlation coefficient (r) can be calculated to determine whether a linear relationship exists between variables and how strong that relationship is

  • Perfect correlation occurs when all of the data points lie on a straight line; this will give a correlation coefficient of 1 or -1

    • +1 = a completely positive correlation

    • -1 = a completely negative correlation

  • A less-than perfect correlation will give a correlation coefficient between 1 and 0, or between 0 and -1

    • The closer to +1, or -1, the coefficient is, the stronger the correlation

  • If there is no correlation between variables the correlation coefficient will be 0

• Correlation coefficients are used in the specification when evaluating data on coronary heart disease

A strong correlation will have a correlation coefficient close to 1, a weak correlation will have a correlation coefficient close to 0, while a lack of any correlation will give a correlation coefficient of 0

Statistical tests

• Statistical tests are used to assess whether or not a data set supports a particular hypothesis. e.g.

  • A null hypothesis will state that there is no significant difference, or association, between two variables

  • An alternative hypothesis will state that there is a significant difference, or association, between two variables

• Statistical analysis allows researchers to accept or reject the null hypothesis

• If a statistical test shows that there is no significant difference, or association, between variables, then it is said that any visible difference is due to chance alone

• Different statistical tests are used for different types of data set, e.g.

  • A t-test determines whether the means of two data sets differ significantly

  • A correlation test determines the presence and strength of a correlation

  • A chi-squared test determines whether the difference between observed and expected values is significant

• You should be able to select and apply the correct statistical test

• The chi-squared test is used in the specification as follows:

  • To test for difference between observed and expected outcomes of a genetic cross

  • To test for association between species