Estimating Population Size (DP IB Biology)

Random Sampling

• Finding out about the abundance and distribution of populations can be achieved by counting all of the organisms present in a habitat

• This is possible for areas that are very small or where the species involved is very large

• For larger and more complex habitats it is not possible to find, identify, and count every organism that is present

• When this is the case, sampling can be used to make an estimate for the total species numbers

  • Sampling involves measuring small samples of a population that act to represent the whole population

Sampling

• Sampling is a method of investigating the abundance and distribution of populations
  

• There are two different types of sampling

  • Random

  • Systematic

• In random sampling the positions of the sampling points are selected at random

  • This method avoids bias by the person that is carrying out the sampling

  • Bias can affect the results, e.g.

    • A student might choose to carry out samples in a particular location because it looks interesting, and this might give the impression that the habitat contains more species than it really does

• In systematic sampling the positions of the sampling points are located at fixed intervals throughout the sampling site

  • This avoids accidentally missing out sections of habitat due to chance

  • Systematic sampling allows researchers to investigate the effect of the presence of certain environmental features on species distribution, e.g. by taking samples along a line that extends away from an environmental feature such as a river

    • A line of this type is known as a transect

• When a sampling area is reasonably uniform then random sampling is the best choice

• Random sample sites can be selected by

  • Laying out a grid over the area to be studied

  • Generating random number co-ordinates 

  • Placing sample sites in the grid squares that match the random number co-ordinates

Random & systematic sampling diagram

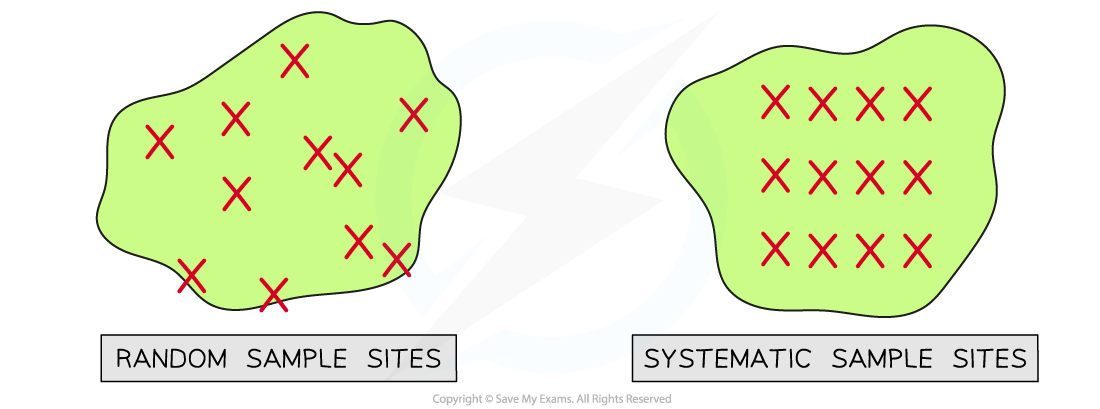
Random sampling involves selecting sample sites at random while systematic sampling involves placing sample sites at regular intervals

NOS: Students should be aware that random sampling, instead of measuring an entire population, inevitably results in sampling error

• A population estimate that is based on sampling makes the assumption that individuals are distributed evenly across the sample site, e.g.

  • Random sampling may happen to miss an area of a site in which no individuals are present; this will result in an overestimate of population size

  • Random sampling may happen to miss an area of a site where many individuals are present; this will result in an underestimate of population size

• There are many factors that influence the distribution of a population, so an even distribution is very unlikely, and so the chance of sampling error occurring when calculating such an estimate is very high

  • A sampling error is the difference between an estimated population size and a true population size

  • This occurs when a sample is not truly representative of a whole population

• Sampling error can be minimised by good investigation design, e.g. carrying out the right type of sampling and taking a large enough sample size

• When scientists write about their findings they must include details of any experimental methods used; this allows their readers to evaluate any error that may be present in the results

Random Quadrat Sampling

Sampling using frame quadrats

• A frame quadrat is a square frame that is placed within the area to be studied to provide a sample

  • Quadrats are used to study the distribution of sessile organisms

  • Quadrats can be different sizes depending on the species being studied

    • A 1 m² quadrat can be used to study small organisms such as herbaceous plants in a grassland or limpets on a rocky shore

    • A 400 m² quadrat can be used to study large organisms such as trees

      • Quadrats like this will usually be marked out with string rather than a frame!

• Frame quadrats can be placed in a habitat randomly, e.g. using random co-ordinates, or systematically, e.g. along a transect

Frame quadrat diagram

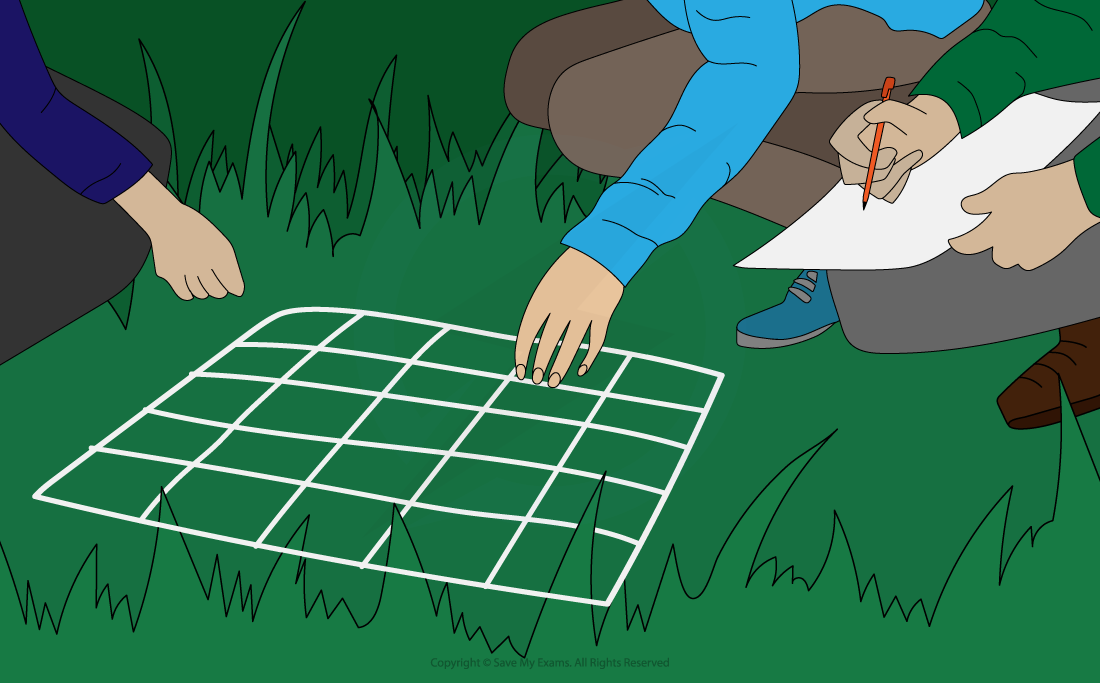
A frame quadrat can be used to measure abundance and distribution

• Scientists can record different types of data from a frame quadrat depending on the aim of a study and the species involved

  • Presence or absence of a species

  • Species frequency; how many individuals are in the quadrat

  • Species abundance; measured on a scale called the ACFOR scale on which species are recorded as being abundant, common, frequent, occasional, rare, or none

  • Percentage cover; the percentage of the quadrat covered by a species

    • Quadrats can be divided up into smaller squares to allow percentage cover to be assessed more easily

Recording percentage cover diagram

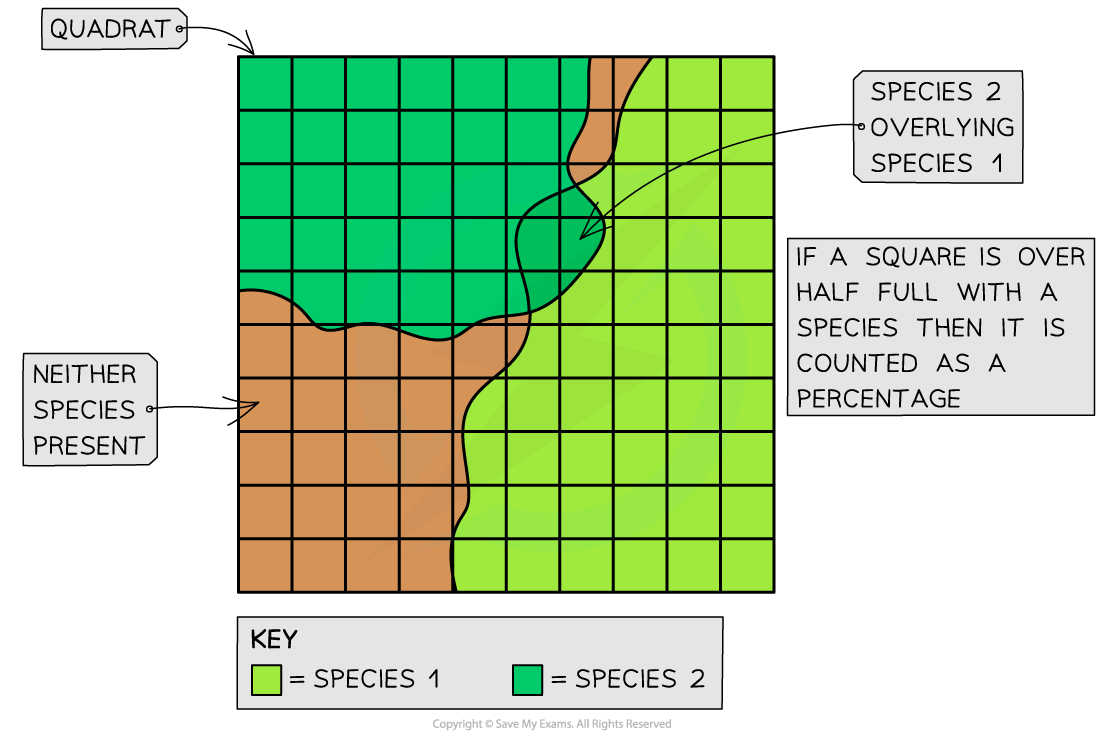
Abundance in a frame quadrat can be assessed by measuring percentage cover

Analysing results

• Quantitative investigations of variation can involve the interpretation of mean values and their standard deviations

  • A mean value describes the average value of a data set

  • Standard deviation is a measure of the spread or dispersion of data around the mean

    • A small standard deviation indicates that the results lie close to the mean, so there is little variation

    • A large standard deviation indicates that the results are more spread out around the mean, so there is a lot of variation

• In the quadrat study described here, a mean could be calculated for the number of individuals of a species found in each quadrat, and then the standard deviation could be calculated to find out how spread out the data points are around the mean

  • This would give an indication of how evenly distributed the population is across the habitat

Small vs large standard deviation graph

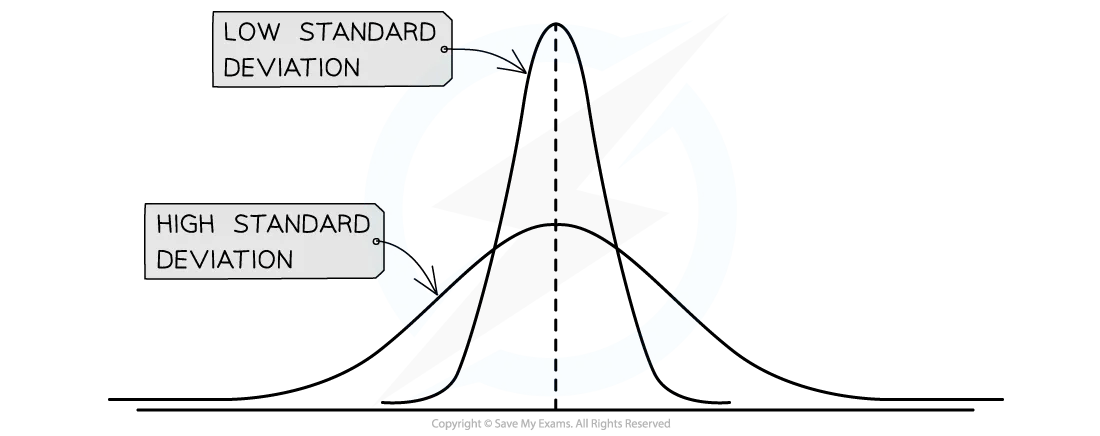
A small standard deviation shows that data are closely grouped around the mean while a large standard deviation shows that data are spread widely around the mean

Estimating Population Size: Motile Organisms

Capture-mark-release-recapture

• The sampling methods described above are only useful for non-motile (sessile) organisms

• Different methods are required for estimating the number of individuals in a population of motile organisms

  • The mark-release-recapture method can be used

• The mark-release-recapture method is carried out as follows:

  • The first large sample is taken; as many individuals as possible are caught, counted and marked in a way that won’t affect their survival

    • e.g. if studying a species of beetle, a small amount of brightly coloured non-toxic paint can be applied to their wing cases

  • The marked individuals are returned to their habitat and allowed to randomly mix with the rest of the population

  • When a sufficient time period has passed another large sample is captured

  • The number of marked and unmarked individuals within the sample are counted

  • The proportion of marked to unmarked individuals is used to calculate an estimate of the population size using a statistical measure known as the Lincoln index

Population size = M × 

• Where:

  • M = number of marked individuals in the first sample

  • N = total number of individuals in the second sample (marked and unmarked)

  • R = number of marked individuals recaptured in the second sample

• The Lincoln index makes some assumptions about the population and the capture-mark-release-recapture method:

  • The marked individuals disperse and mix back in fully with the main population

  • The marking doesn't affect the survival rates of the marked individuals, e.g. doesn't make them more visible and therefore more likely to be predated

  • The marking remains visible throughout the sampling and doesn't rub off

  • The population stays the same size during the study period, i.e.

    • There are no significant changes in population size due to births and deaths

    • There are no migrations into or out of the main population