Estimating Population Size (DP IB Biology) : Revision Note
Random Sampling
Finding out about the abundance and distribution of populations can be achieved by counting all of the organisms present in a habitat
This is possible for areas that are very small or where the species involved is very large
For larger and more complex habitats it is not possible to find, identify, and count every organism that is present
When this is the case, sampling can be used to make an estimate for the total species numbers
Sampling involves measuring small samples of a population that act to represent the whole population
Sampling
Sampling is a method of investigating the abundance and distribution of populations
There are two different types of sampling
Random
Systematic
In random sampling the positions of the sampling points are selected at random
This method avoids bias by the person that is carrying out the sampling
Bias can affect the results, e.g.
A student might choose to carry out samples in a particular location because it looks interesting, and this might give the impression that the habitat contains more species than it really does
In systematic sampling the positions of the sampling points are located at fixed intervals throughout the sampling site
This avoids accidentally missing out sections of habitat due to chance
Systematic sampling allows researchers to investigate the effect of the presence of certain environmental features on species distribution, e.g. by taking samples along a line that extends away from an environmental feature such as a river
A line of this type is known as a transect
When a sampling area is reasonably uniform then random sampling is the best choice
Random sample sites can be selected by
Laying out a grid over the area to be studied
Generating random number co-ordinates
Placing sample sites in the grid squares that match the random number co-ordinates
Random & systematic sampling diagram
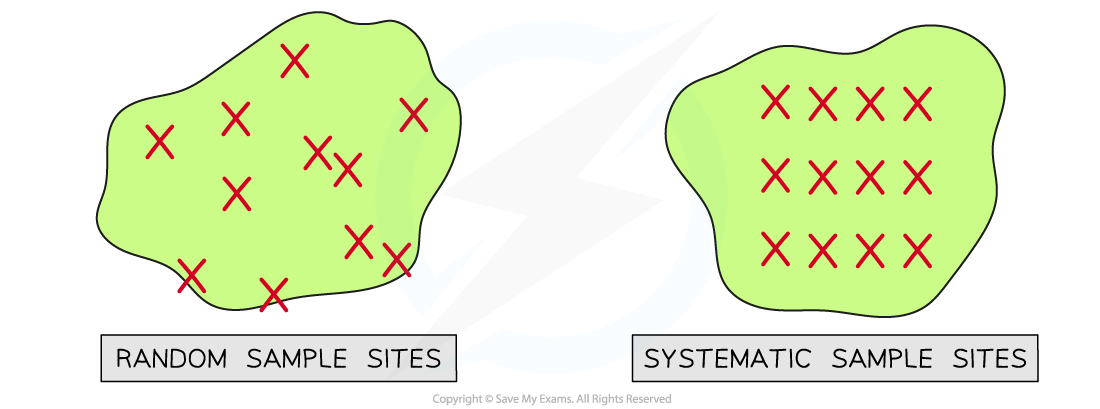
Random sampling involves selecting sample sites at random while systematic sampling involves placing sample sites at regular intervals
NOS: Students should be aware that random sampling, instead of measuring an entire population, inevitably results in sampling error
A population estimate that is based on sampling makes the assumption that individuals are distributed evenly across the sample site, e.g.
Random sampling may happen to miss an area of a site in which no individuals are present; this will result in an overestimate of population size
Random sampling may happen to miss an area of a site where many individuals are present; this will result in an underestimate of population size
There are many factors that influence the distribution of a population, so an even distribution is very unlikely, and so the chance of sampling error occurring when calculating such an estimate is very high
A sampling error is the difference between an estimated population size and a true population size
This occurs when a sample is not truly representative of a whole population
Sampling error can be minimised by good investigation design, e.g. carrying out the right type of sampling and taking a large enough sample size
When scientists write about their findings they must include details of any experimental methods used; this allows their readers to evaluate any error that may be present in the results
Random Quadrat Sampling
Sampling using frame quadrats
A frame quadrat is a square frame that is placed within the area to be studied to provide a sample
Quadrats are used to study the distribution of sessile organisms
Quadrats can be different sizes depending on the species being studied
A 1 m² quadrat can be used to study small organisms such as herbaceous plants in a grassland or limpets on a rocky shore
A 400 m² quadrat can be used to study large organisms such as trees
Quadrats like this will usually be marked out with string rather than a frame!
Frame quadrats can be placed in a habitat randomly, e.g. using random co-ordinates, or systematically, e.g. along a transect
Frame quadrat diagram
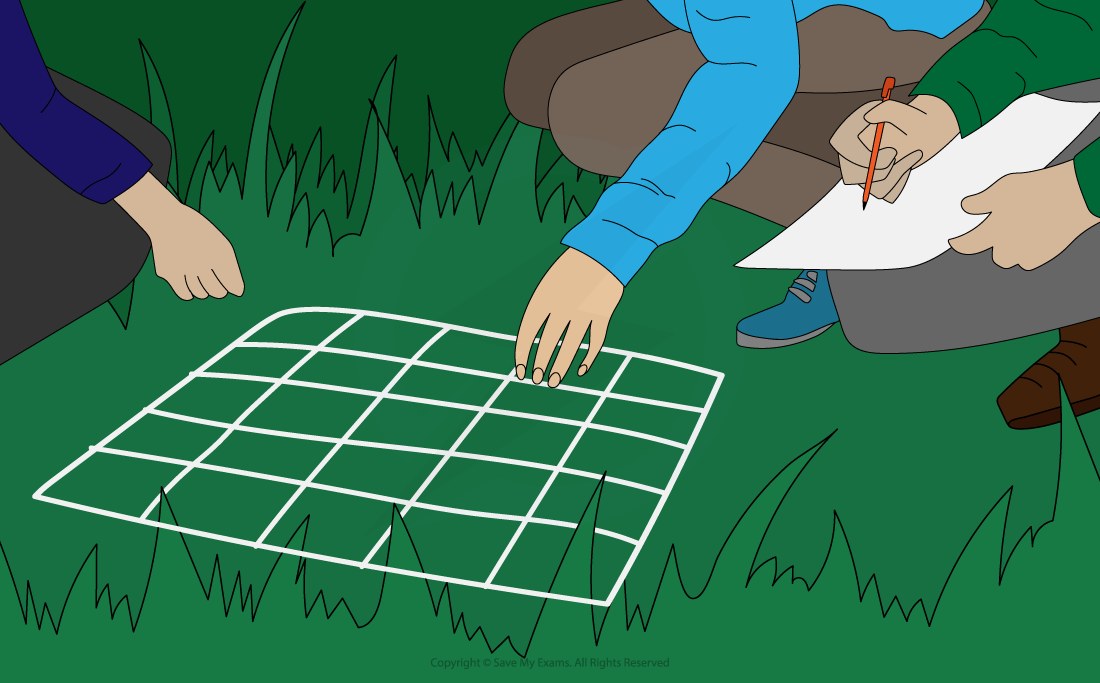
A frame quadrat can be used to measure abundance and distribution
Scientists can record different types of data from a frame quadrat depending on the aim of a study and the species involved
Presence or absence of a species
Species frequency; how many individuals are in the quadrat
Species abundance; measured on a scale called the ACFOR scale on which species are recorded as being abundant, common, frequent, occasional, rare, or none
Percentage cover; the percentage of the quadrat covered by a species
Quadrats can be divided up into smaller squares to allow percentage cover to be assessed more easily
Recording percentage cover diagram
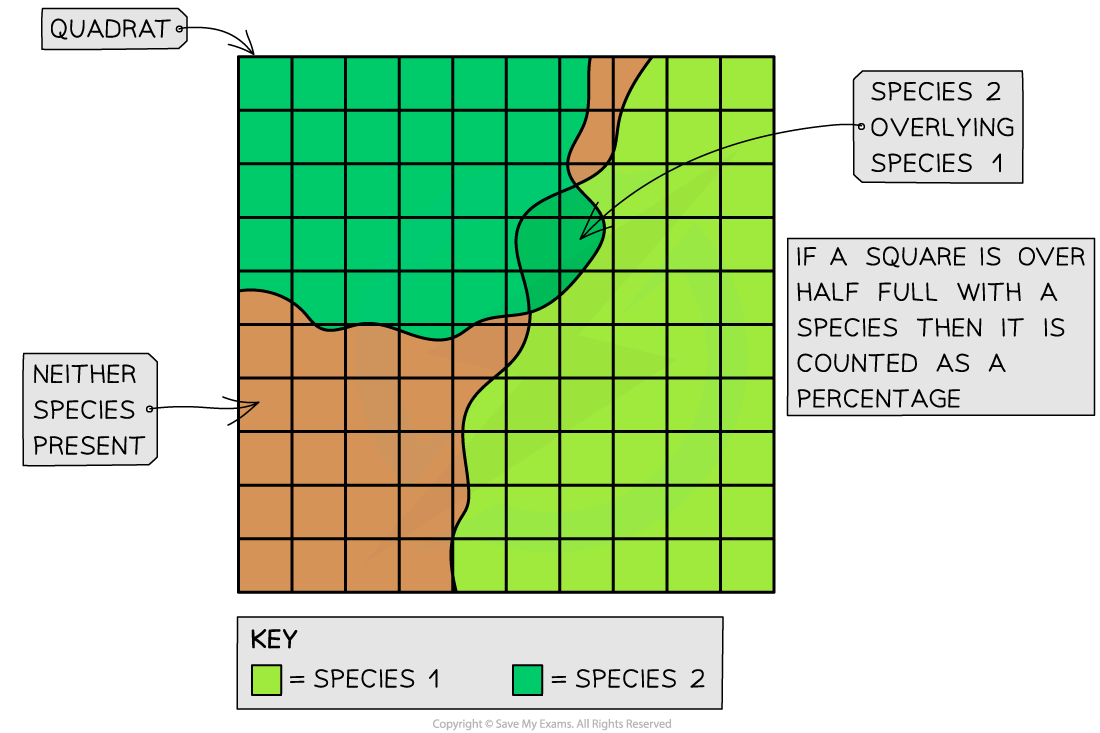
Abundance in a frame quadrat can be assessed by measuring percentage cover
Analysing results
Quantitative investigations of variation can involve the interpretation of mean values and their standard deviations
A mean value describes the average value of a data set
Standard deviation is a measure of the spread or dispersion of data around the mean
A small standard deviation indicates that the results lie close to the mean, so there is little variation
A large standard deviation indicates that the results are more spread out around the mean, so there is a lot of variation
In the quadrat study described here, a mean could be calculated for the number of individuals of a species found in each quadrat, and then the standard deviation could be calculated to find out how spread out the data points are around the mean
This would give an indication of how evenly distributed the population is across the habitat
Small vs large standard deviation graph
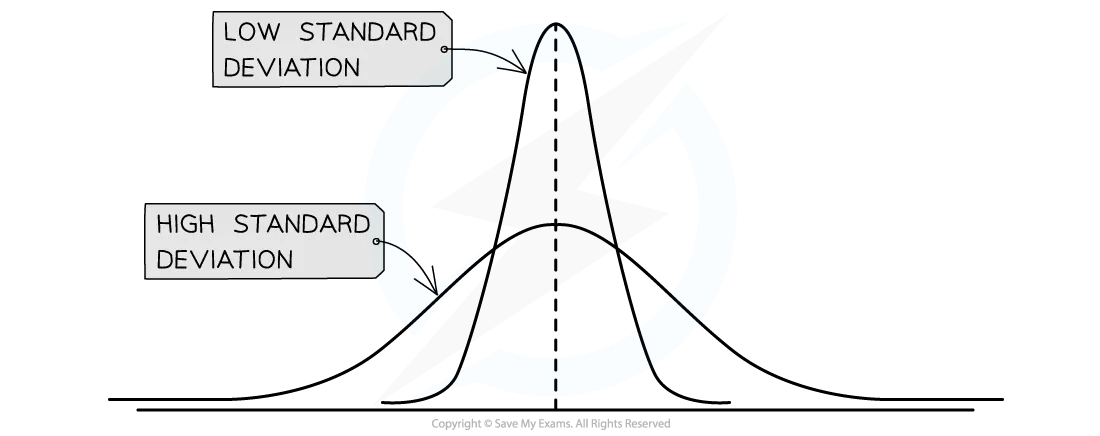
A small standard deviation shows that data are closely grouped around the mean while a large standard deviation shows that data are spread widely around the mean
Estimating Population Size: Motile Organisms
Capture-mark-release-recapture
The sampling methods described above are only useful for non-motile (sessile) organisms
Different methods are required for estimating the number of individuals in a population of motile organisms
The mark-release-recapture method can be used
The mark-release-recapture method is carried out as follows:
The first large sample is taken; as many individuals as possible are caught, counted and marked in a way that won’t affect their survival
e.g. if studying a species of beetle, a small amount of brightly coloured non-toxic paint can be applied to their wing cases
The marked individuals are returned to their habitat and allowed to randomly mix with the rest of the population
When a sufficient time period has passed another large sample is captured
The number of marked and unmarked individuals within the sample are counted
The proportion of marked to unmarked individuals is used to calculate an estimate of the population size using a statistical measure known as the Lincoln index
Population size = M ×
Where:
M = number of marked individuals in the first sample
N = total number of individuals in the second sample (marked and unmarked)
R = number of marked individuals recaptured in the second sample
Worked Example
Scientists wanted to investigate the abundance of leafhoppers in a small grassy meadow.
They used nets to catch a large sample of leafhoppers. Each insect was marked on its underside with non-toxic, waterproof paint and then released back into the meadow.
The following week another large sample was caught using sweep nets.
Use the figures below to estimate the size of the leafhopper population in this meadow.
No. caught and marked in first sample (M) = 236
No. caught in second sample (N) = 244
No. of marked individuals recaptured in the second sample (R) = 71
Answer:
Step One: Write out the Lincoln index equation and substitute in the known values
N = M x
N = 236 ×
Step Two: Calculate the population size estimate (N)
N = 236 x 3.44
N = 811.84
= 812 (to the nearest whole organism)
The Lincoln index makes some assumptions about the population and the capture-mark-release-recapture method:
The marked individuals disperse and mix back in fully with the main population
The marking doesn't affect the survival rates of the marked individuals, e.g. doesn't make them more visible and therefore more likely to be predated
The marking remains visible throughout the sampling and doesn't rub off
The population stays the same size during the study period, i.e.
There are no significant changes in population size due to births and deaths
There are no migrations into or out of the main population

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
