Population Growth Curves: Skills (DP IB Biology)

Population Growth Curves

• Populations of living organisms tend to follow a set growth pattern over time; this growth pattern gives rise to a population growth curve that can be plotted on a graph

• Population growth curves can generally be seen in any newly established or recovering population, e.g.

  • Antarctic fur seals were hunted extensively during the 1800s, and underwent a population recovery following the end of this practice

  • The recovery of the seal population in some locations follows a classic growth curve, e.g. in the graph below for seals on Cape Shirreff, Antarctica

    • Pup count is used to represent the size of the seal population

  • Note that this recovery has not continued throughout the early 21st century, with climate change having since caused severe declines in many seal populations

Antarctic fur seal growth curve graph

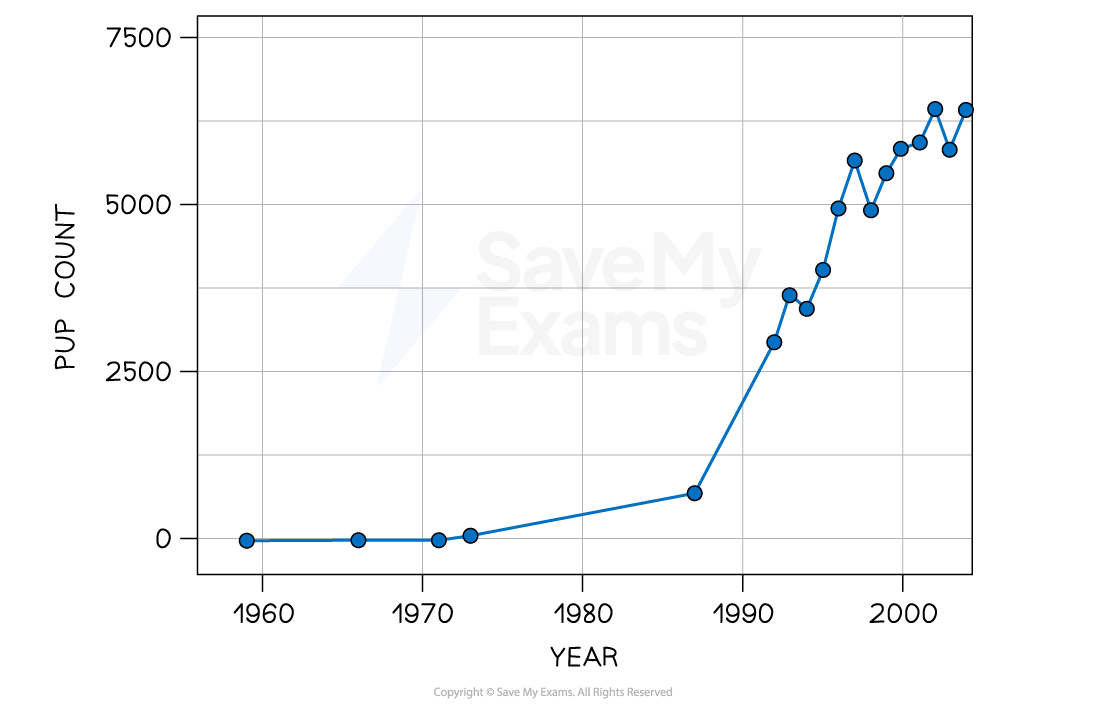
The Antarctic fur seal population in Cape Shirreff, Antarctica, followed a classic growth curve between 1960 and the early 2000s

• The population growth curve shown above is an example of a sigmoid, or s-shaped, growth curve

• Such curves contain three phases:

  • Exponential phase

    • Also known as the logarithmic phase

    • Here there are no factors that limit population growth, so the population increases exponentially

    • The number of individuals increases, and so does the rate of growth

  • Transition phase

    • Limiting factors start to act on the population, e.g. competition increases and predators are attracted to large prey populations

    • The rate of growth slows, though the population is still increasing

  • Plateau phase

    • Also known as the stationary phase

    • Limiting factors cause the death rate to equal the birth rate and population growth stops

    • This plateau occurs at the carrying capacity

    • The population size often fluctuates slightly around the carrying capacity

Population growth curve graph

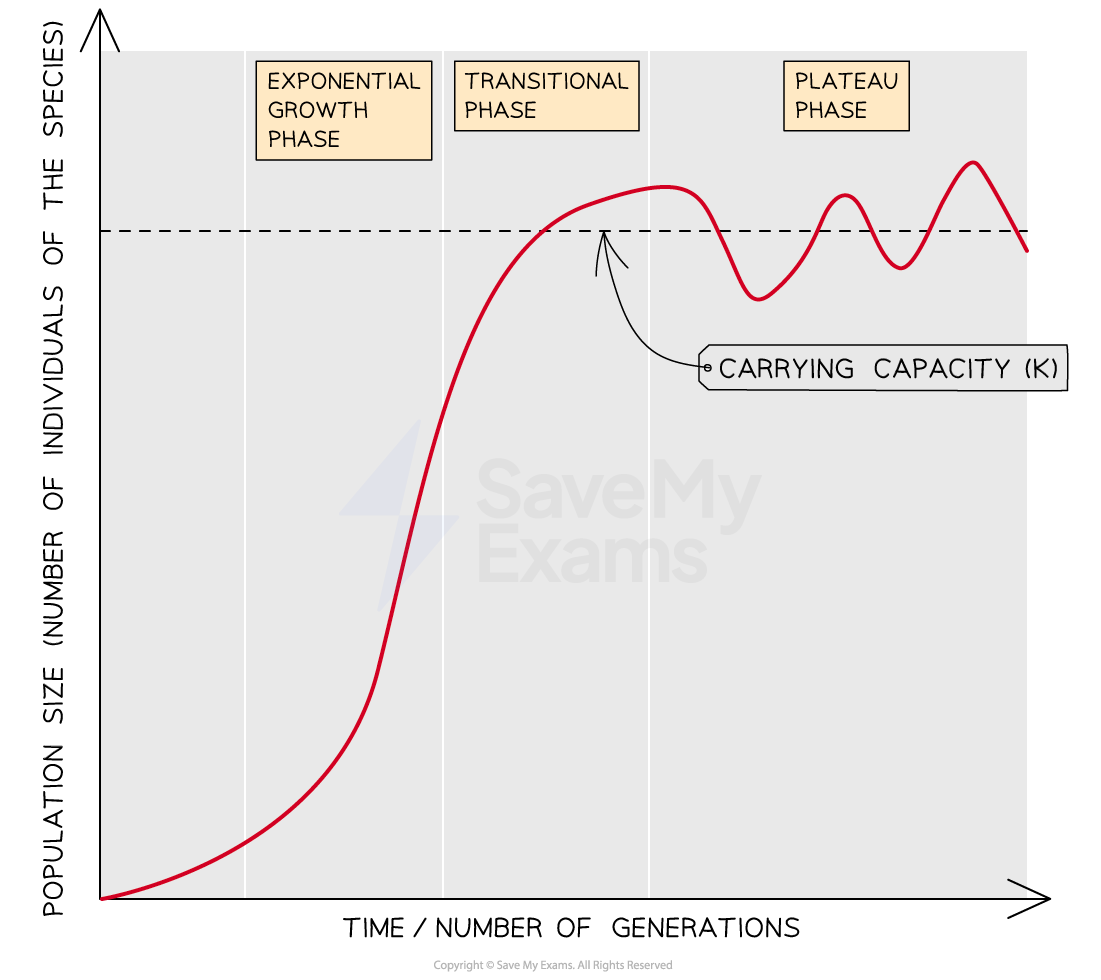
Sigmoidal population growth curves show an exponential growth phase, a transitional phase and a plateau phase

NOS: The curve represents an idealised graphical model

• Scientists use models to represent real world ideas, organisms, processes and systems that cannot be easily investigated

• Models are useful for the purposes of experimentation and testing predictions, but they are not perfect representations of biological systems

• Here, the population growth model is useful for conceptualising the different stages in the growth of a population, but scientists must always be aware that real ecosystems are complex and that there are many factors at play in determining population size

• There are few real-world situations where populations follow perfect sigmoid growth curves, and the seal population example given above soon showed population decline rather than remaining at a plataeu

Exponential Population Growth

Testing for exponential growth with a logarithmic scale

• Population growth is exponential when the speed of growth is proportional to the number of individuals, i.e. a population of 20 individuals will reproduce at twice the rate of a population of 10 individuals

• It is possible to assess whether or not exponential growth is occurring by plotting population size (y) against time (x) on a graph with a logarithmic scale on the y axis and a non-logarithmic scale on the x axis

  • Logarithmic scales can be very useful when investigating factors that vary over several orders of magnitude, e.g. population size

    • 'Orders of magnitude' refers to whether values are measured in, e.g. tens, hundreds, thousands etc.; using a log scale allows tens and millions to be represented on the same easily visible scale

  • The numbers in a logarithmic scale represents logarithms, or powers, of a base number

  • If using a log₁₀ scale, in which the base number is 10, the numbers on the y-axis represent a power of 10, e.g. 1=10¹ (10), 2=10² (100), 3=10³ (1000) etc.

  • Logarithmic scales allow for a wide range of values to be displayed on a single graph

• An exponentially growing population plotted with a log scale on the y axis will appear as a straight line:

Exponential population growth on a logarithmic scale graph

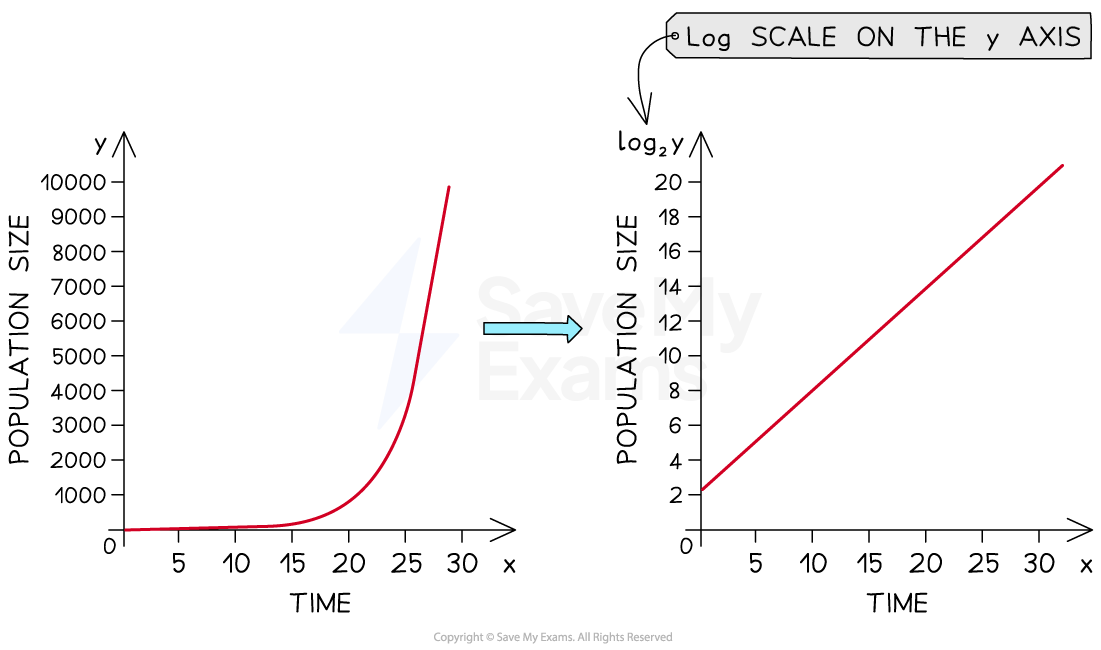
An exponentially growing population plotted with a log scale on the y axis will appear as a straight line

Modelling the Sigmoid Growth Curve

• Organisms that grow and reproduce under laboratory conditions can be used to model the sigmoid population growth curve

• Suitable organisms include:

  • Yeast

  • Duckweed

Modelling population growth curves using yeast

• The population growth rate of microorganisms, such as bacteria or yeast, can be investigated by growing the microorganisms in a broth culture

• The turbidity of the suspension can then be used as a way of estimating the number of cells, i.e. the population size, of the microorganisms in the broth culture

  • Turbidity is a measure of the cloudiness of a suspension, i.e. how much light can pass through it

• As the microorganisms in the broth culture reproduce and their population grows, the suspension becomes progressively more turbid

• This changing turbidity can be monitored by measuring how much light can pass through the suspension at fixed time intervals after the initial inoculation of the nutrient broth with the microorganisms

• A turbidity meter or a colorimeter, connected to a datalogger, can be used to take these measurements

• The results can then be used to plot a population growth curve to show how the population of microorganism changes over time

Yeast population growth on a logarithmic scale graph

Turbidity measurements can be used to gain a measure of yeast population size over time; the resulting data can be plotted using a log scale to show exponential population growth

Modelling population growth curves using duckweed

• Duckweed is a type of pond weed that grows on the surface of still bodies of fresh water

• It is ideal for modelling population growth because it reproduces quickly and asexually, and newly produced fronds, also known as thalli (singular thallus), remain attached to the parent fronds in clusters, allowing for easy counting

• Population growth can be modelled using duckweed as follows:

  1. Place a small number of duckweed fronds into a petri dish that contains distilled water mixed with liquid fertiliser

  2. Place the petri dishes in a brightly lit location, but out of direct sunlight

  3. Record the number of duckweed fronds present after 1 week

  4. Repeat the counting process once a week for a total of six weeks, topping up the dish with distilled water as needed

  5. Plot the results on a graph to show a population growth curve

CC BY-SA 3.0, via Wikimedia Commons

Duckweed grows on the surface of fresh water, and its easily distinguishable thalli can be easily counted in a laboratory setting