Total Internal Reflection (OCR AS Physics) : Revision Note
Total Internal Reflection
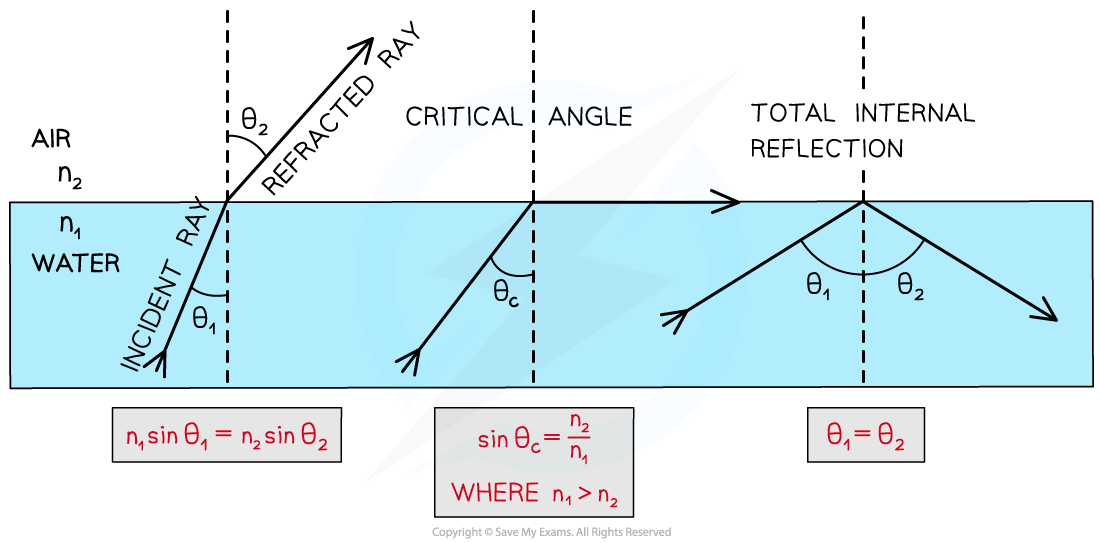
As the angle of incidence is increased, the angle of refraction also increases until it gets closer to 90°
When the angle of refraction is exactly 90° the light is refracted along the boundary
At this point, the angle of incidence is known as the critical angle C
This angle can be found using the formula:
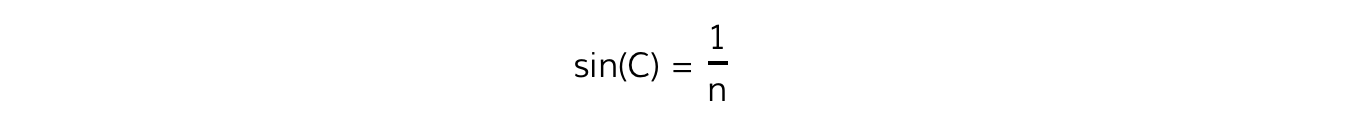
This can easily be derived from Snell’s law where:
θ1 = C
θ2 = 90°
n1 = n
n2 = 1 (air)
Total internal reflection (TIR) occurs when:
The angle of incidence is greater than the critical angle and the incident refractive index n1 is greater than the refractive index of the material at the boundary n2
Therefore, the two conditions for total internal reflection are:
The angle of incidence, θ1 > the critical angle, C
Refractive index n1 > refractive index n2 (air)
Worked Example
A glass cube is held in contact with a liquid and a light ray is directed at a vertical face of the cube. The angle of incidence at the vertical face is 39° and the angle of refraction is 25° as shown in the diagram. The light ray is totally internally reflected at X.
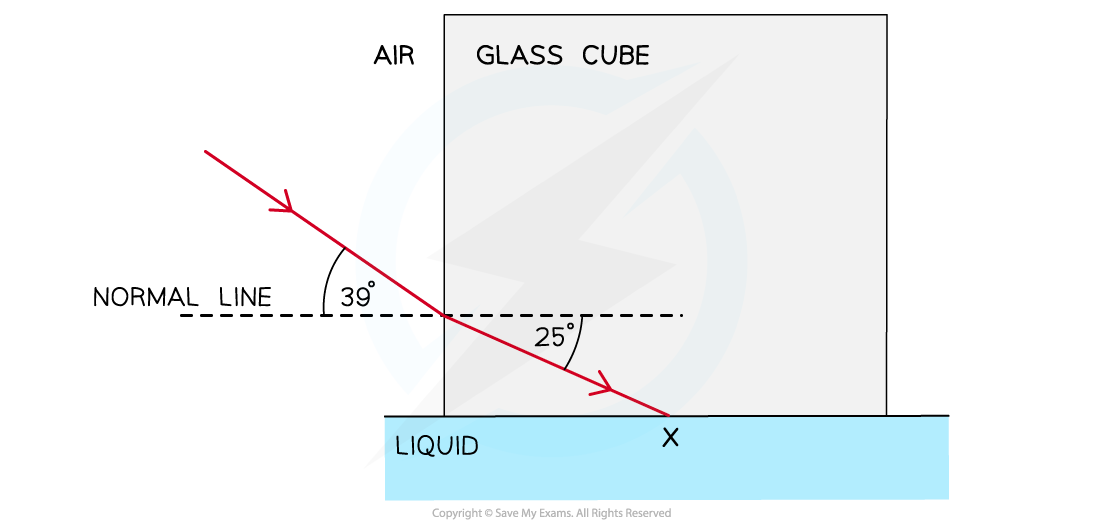
Complete the diagram to show the path of the ray beyond X to the air and calculate the critical angle for the glass-liquid boundary.
Answer:
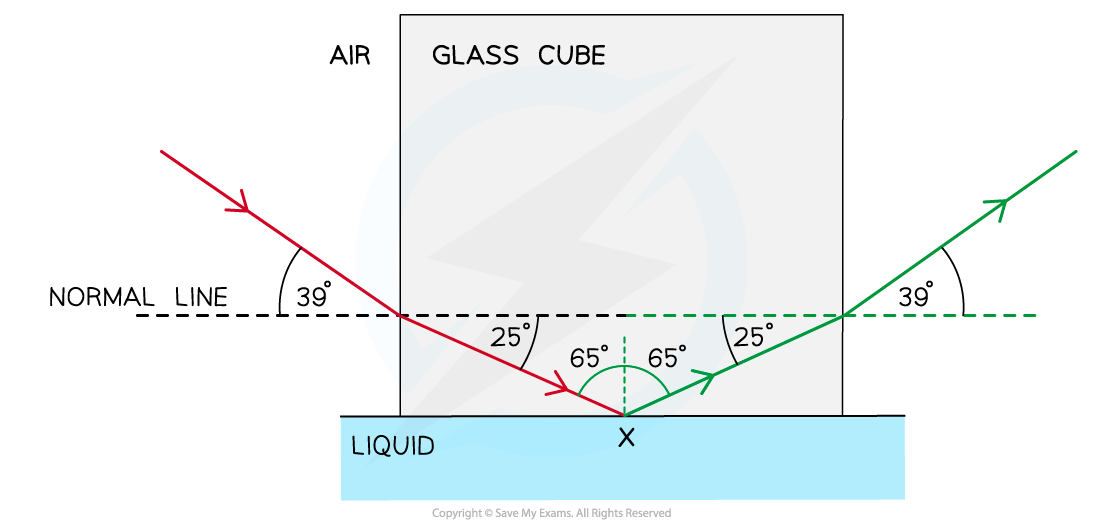
Step 1: Draw the reflected angle at the glass-liquid boundary
When a light ray is reflected, the angle of incidence = angle of reflection
Therefore, the angle of incidence (and reflection) is 90° – 25° = 65°
Step 2: Draw the refracted angle at the glass-air boundary
At the glass-air boundary, the light ray refracts away from the normal
Due to the reflection, the light rays are symmetrical to the other side
Step 3: Calculate the critical angle
The question states the ray is “totally internally reflected for the first time” meaning that this is the lowest angle at which TIR occurs
Therefore, 65° is the critical angle
Examiner Tips and Tricks
Always draw ray diagrams with a ruler, and make sure you're comfortable calculating unknown angles. The main rules to remember are:
Angles in a right angle add up to 90°
Angles on a straight line add up to 180°
Angles in any triangle add up to 180°
For angles in parallel lines, such as alternate and opposite angles, take a look at the OCR GCSE maths revision notes '7.1.1 Angles in Parallel Lines'

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
