The de Broglie Equation
- Using ideas based upon the quantum theory and Einstein’s theory of relativity, de Broglie related the momentum of a particle to its wavelength
- This is known as the de Broglie equation:
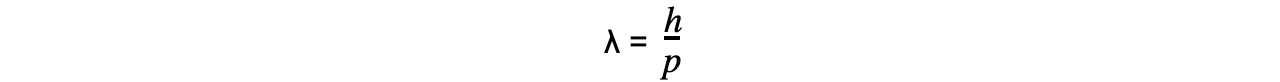
- Where:
- λ = the de Broglie wavelength (m)
- h = Planck's Constant (J s)
- p = momentum (kg m s-1)
- The de Broglie equation, therefore, links a particle-like property (momentum) to a wave-like property (wavelength) demonstrating wave-particle duality for all particles
- Since momentum p = mv, the de Broglie wavelength can be related to the speed of a moving particle (v) by the equation:
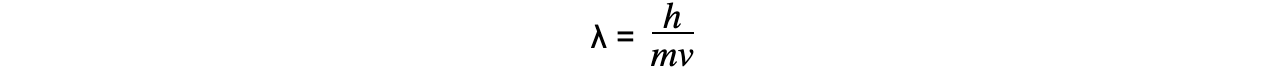
- Since kinetic energy E is equal to
E = ½ mv2
- Momentum and kinetic energy can be related by:
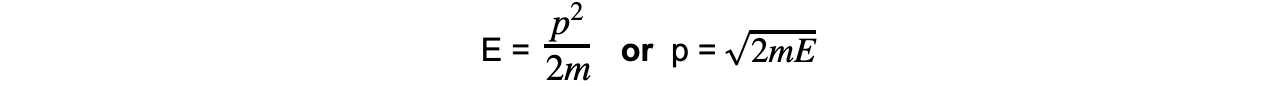
- Combining this with the de Broglie equation gives a form that relates the de Broglie wavelength of a particle to its kinetic energy:
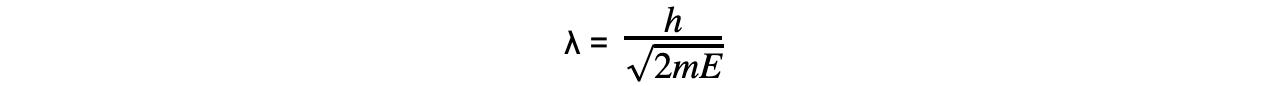
- Where:
- E = kinetic energy of the particle (J)
- m = mass of the particle (kg)
- v = speed of the particle (m s-1)
Worked example
A proton and an electron are each accelerated from rest through the same potential difference. Determine the ratio:
- Mass of a proton = 1.67 × 10–27 kg
- Mass of an electron = 9.11 × 10–31 kg
Examiner Tip
If you've not been given the mass of a particle in a question, make sure to look at your data sheet which includes the rest mass of various particles
