The Photoelectric Equation (OCR AS Physics) : Revision Note
Interaction Between a Photon & Surface Electron
In the photoelectric effect, it is very important to note:
Each surface electron can only interact with a single photon
This provides important evidence that light is quantised or carried in discrete packets
This also means the number of photoelectrons emitted is exactly equal to the number of photons incident on the surface in which the photoelectric effect is taking place
Increasing the intensity of the electromagnetic radiation increases the number of photons per area incident on the surface
From the one-to-one interaction, this also means this increases the number of photoelectrons emitted from the surface
The Photoelectric Equation
Since energy is always conserved, the energy of an incident photon is equal to:
The work function + the maximum kinetic energy of the photoelectron
The energy within a photon is equal to hf
This energy is transferred to the electron to release it from a material (the work function) and the remaining amount is given as kinetic energy to the emitted photoelectron
This equation is known as the photoelectric equation:
E = hf = Φ + ½ mv2max
Where:
h = Planck's constant (J s)
f = the frequency of the incident radiation (Hz)
Φ = the work function of the material (J)
½ mv2max= KEmax = the maximum kinetic energy of the photoelectrons (J)
This equation demonstrates:
If the incident photons do not have a high enough frequency and energy to overcome the work function (Φ), then no electrons will be emitted
hf0 = Φ, where f0 = threshold frequency, photoelectric emission only just occurs
KEmax depends only on the frequency of the incident photon, and not the intensity of the radiation
The majority of photoelectrons will have kinetic energies less than KEmax
Graphical Representation of Work Function
The photoelectric equation can be rearranged into the straight line equation:
y = mx + c
Comparing this to the photoelectric equation:
KEmax = hf - Φ
A graph of maximum kinetic energy KEmax against frequency f can be obtained

The key elements of the graph:
The work function Φ is the y-intercept
The threshold frequency f0 is the x-intercept
The gradient is equal to Planck's constant h
There are no electrons emitted below the threshold frequency f0
Worked Example
The graph below shows how the maximum kinetic energy Ek of electrons emitted from the surface of sodium metal varies with the frequency f of the incident radiation.
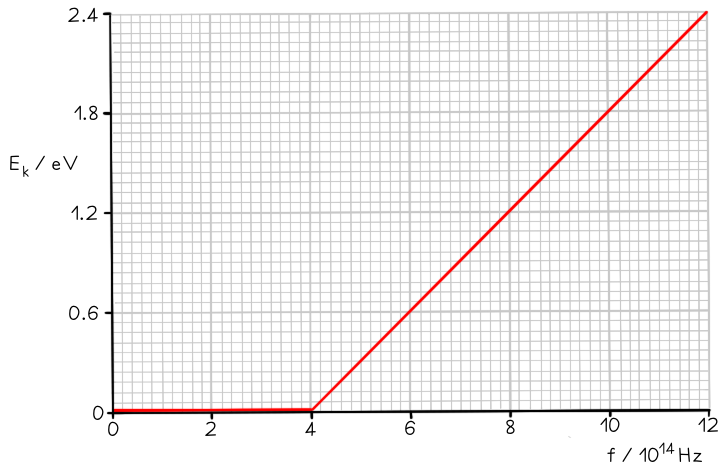
Calculate the work function of sodium in eV.
Answer:
Step 1: Write out the photoelectric equation and rearrange to fit the equation of a
straight line
E = hf = Φ + ½ mv2max → KEmax = hf - Φ
y = mx + c
Step 2: Identify the threshold frequency from the x-axis of the graph
When Ek = 0, f = f0
Therefore, the threshold frequency is f0 = 4 × 1014 Hz
Step 3: Calculate the work function
From the graph at f0, ½ mvmax2 = 0
Φ = hf0 = (6.63 × 10-34) × (4 × 1014) = 2.652 × 10-19 J
Step 4: Convert the work function into eV
1 eV = 1.6 × 10-19 J J → eV: divide by 1.6 × 10-19
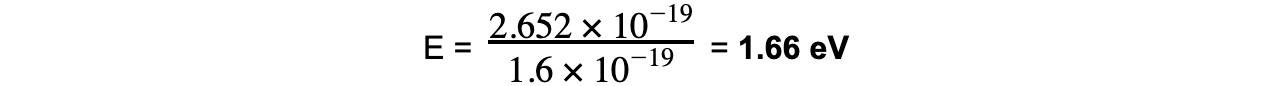
Examiner Tips and Tricks
When using the photoelectric effect equation, hf, Φ and KEmax must all have the same units (joules). Therefore make sure to convert any values given in eV into Joules (× (1.6 × 10-19))

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?
