Stress, Strain & Tensile Strength (OCR AS Physics)

• Opposite forces can deform an object
• If the forces stretch the object, then they are tensile forces
• Tensile forces lead to the two properties of materials known as tensile stress and tensile strain

Tensile Stress

• Tensile stress is defined as the force exerted per unit cross-sectional area of a material

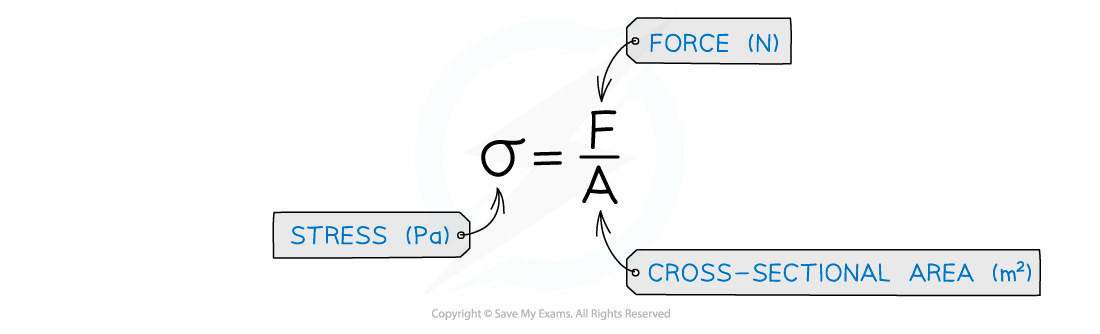
• The ultimate tensile stress is the maximum force per original cross-sectional area a wire is able to support until it breaks
• Stress has the units of pascals (Pa), which is the same units as pressure (also force ÷ area)

Tensile Strain

• Strain is the extension per unit length
• This is a deformation of a solid due to stress in the form of elongation or contraction

• The strain is a dimensionless unit because it’s the ratio of lengths
• Sometimes strain might be written as a percentage
  • For example, extending a 0.1 m wire by 0.005 m would produce a strain of (0.005 ÷ 0.1) × 100 = 5 %

Ultimate Tensile Strength

• The ultimate tensile strength of a material is defined as:

The maximum amount of load or stress a material can handle until it fractures and breaks

• The table lists some common materials and their tensile strength:

Tensile strength of various materials

Part (a)

Step 1: Write down the tensile stress equation

Tensile stress = Force ÷ Cross-sectional area

Step 2: Calculate the cross-sectional area, A of the wire

• • A wire has a circular cross-sectional area = πr²

  Area = π × (0.2 × 10^-3)² =1.2566 × 10^-7 m²

Step 3: Substitute values in the tensile stress equation

Tensile stress = 50 ÷ (1.2566 × 10^-7) = 397.899 × 10⁶ Pa = 400 MPa

Part (b)

Step 1: Write down the tensile strain equation

Tensile strain = Extension ÷ Original length

Step 2: Determine the extension

• • The extension is total length – the original length

Extension = 4.53 – 4.50 = 0.03 m

Step 3: Substitute values in the tensile strain equation

Tensile strain = 0.03 ÷ 4.50 = 6.7 × 10^-3