Analysing Quantitative Data (OCR AS Physics): Revision Note

Analysing Quantitative Data

• Maths is very important throughout the whole of physics

• In particular, maths skills are required when dealing with data from experiments

• The mathematical skills required for the analysis of quantitative data include:

  • Using standard form

  • Quoting to an appropriate number of significant figures

  • Calculating mean values

  • Graph skills

Using Standard Form

• Often, physical quantities will be presented in standard form

• This makes it easier to present numbers that are very large or very small without having to repeat many zeros

  • For example, the speed of light in a vacuum equal to 3.00 × 10⁸ m s⁻¹

• It will also be necessary to know the prefixes for the numbers of ten

Using Significant Figures

• Calculations must be reported to an appropriate number of significant figures

• Also, all the data in a column should be quoted to the same number of significant figures

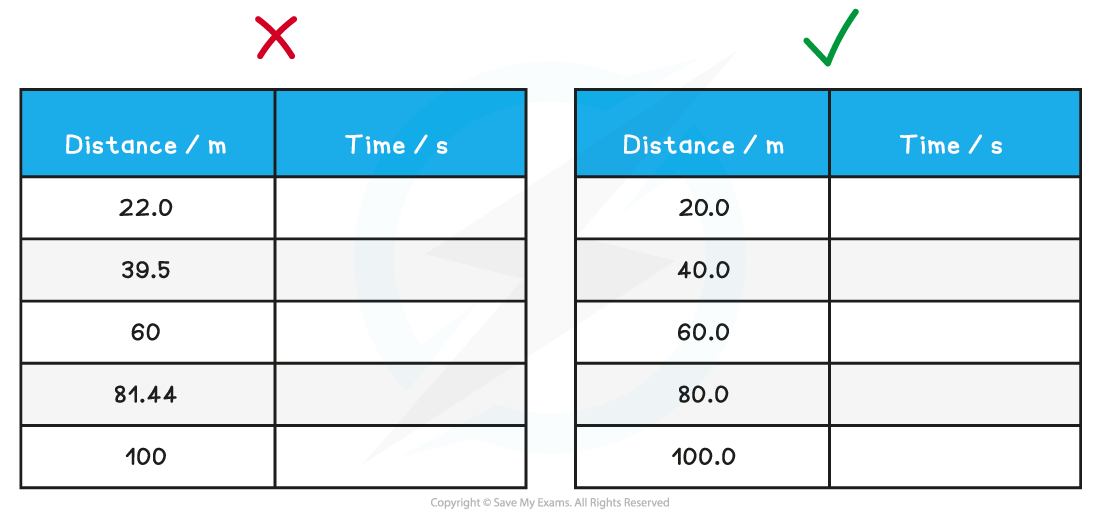
It is important that the significant figures are consistent in data

Calculating Mean Values

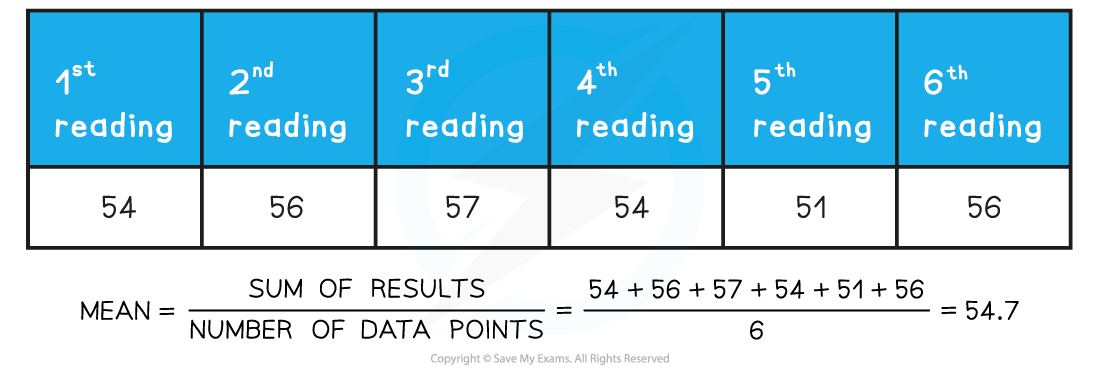
• When several repeat readings are made, it will be necessary to calculate a mean value

• When calculating the mean value of measurements, it is acceptable to increase the number of significant figures by 1

Graph Skills

• In several experiments during A-Level Physics, the aim is generally to find if there is a relationship between two variables

• This can be done by translating information between graphical, numerical, and algebraic forms

  • For example, plotting a graph from data of displacement and time, and calculating the rate of change (instantaneous velocity) from the tangent to the curve at any point

• Graph skills that will be expected during A-Level include:

  • Understanding that if a relationship obeys the equation of a straight-line y = mx + c then the gradient and the y-intercept will provide values that can be analysed to draw conclusions

  • Finding the area under a graph, including estimating the area under graphs that are not linear

  • Using and interpreting logarithmic plots

  • Drawing tangents and calculating the gradient of these

  • Calculating the gradient of a straight-line graph

  • Understanding where asymptotes may be required