Presenting & Interpreting Results (OCR AS Physics) : Revision Note
Presenting Observations & Data
Data can be presented in a variety of ways, such as on graphs, charts, or tables
Tables are applicable to any experiment yielding data
Graphs, on the other hand, are a little trickier depending on the type of data collected e.g. quantitative or qualitative
Quantitative data uses numerical values
Qualitative data is observed but not measured with a numerical value e.g. colour
Presenting Data in a Table
When taking readings, a sensible range should be taken, and the values should all be stated to an appropriate number of significant figures or decimal places
This is usually the same number as the resolution of the measuring instrument
The columns in any table should have both a quantity and a unit in their heading
When labelling columns, the names of the quantities should be separated from their unit by a forward slash ( / )
For data displayed in a table:
The first column should contain the independent variable
The second column should contain the dependent variable
If repeat readings of the dependent variable are required, these should be included with a column for the mean value at the end
Any columns required for processing data e.g. calculations should come after this

Conventions for presenting data in a table. The length is the independent variable and the frequency is the dependent variable
Presenting Data on a Graph
All readings, including suspected anomalous results, should be plotted on a graph so that they can be easily identified
When taking repeat readings, it is the mean value that is plotted
The way data is presented on a graph depends on what type of data it is
Discrete data
Only certain values can be taken, normally a whole number e.g. number of students
This should be displayed on a scatter graph or bar chart
Continuous data
Can take any value on a scale e.g. voltage in a circuit
This should be displayed on a line or scatter graph
Categorical data
Values that can be sorted into categories e.g. types of material
This should be displayed on a pie or bar chart
Ordered data
Data that can be put in ordered categories e.g. low, medium, high
This should be displayed on a bar chart
Processing, Analysing & Interpreting Experimental Results
After an experiment has been carried out, sometimes the raw results will need to be processed before they are in a useful or meaningful format
Sometimes, various calculations will need to be carried out in order to get the data in the form of a straight line
This is normally done by comparing the equation to that of a straight line: y = mx + c
Worked Example
A student measures the background radiation count in a laboratory and obtains the following readings:

The student is trying to verify the inverse square law of gamma radiation on a sample of Radium-226. He collects the following data:
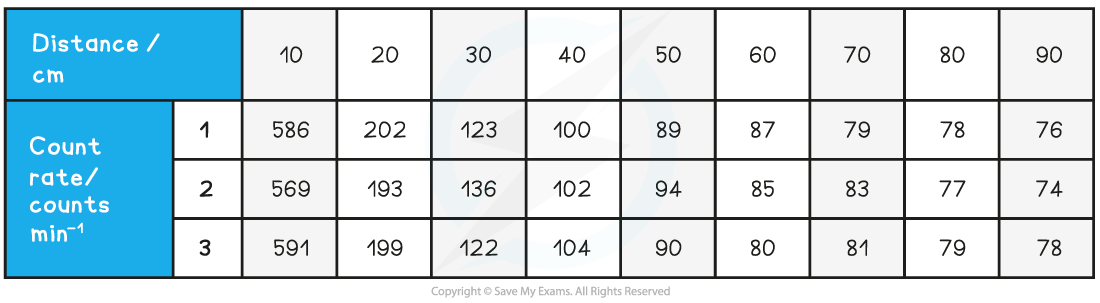
Use this data to determine if the student’s data follows an inverse square law.
Answer:
Step 1: Determine a mean value of background radiation
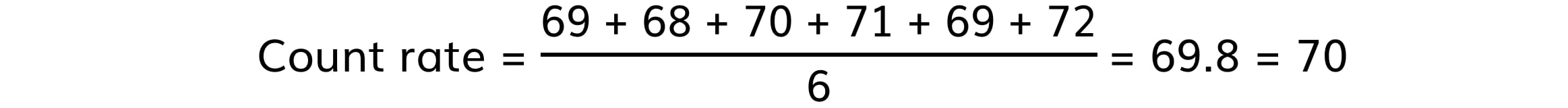
The background radiation must be subtracted from each count rate reading to determine the corrected count rate, C
Step 2: Compare the inverse square law to the equation of a straight line
According to the inverse square law, the intensity, I, of the γ radiation from a point source depends on the distance, x, from the source
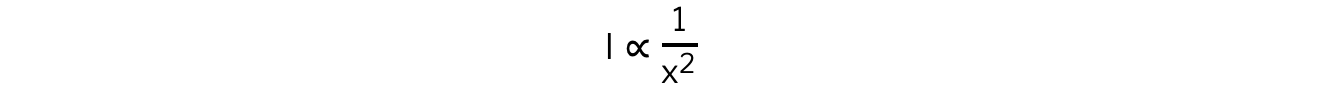
Intensity is proportional to the corrected count rate, C, so
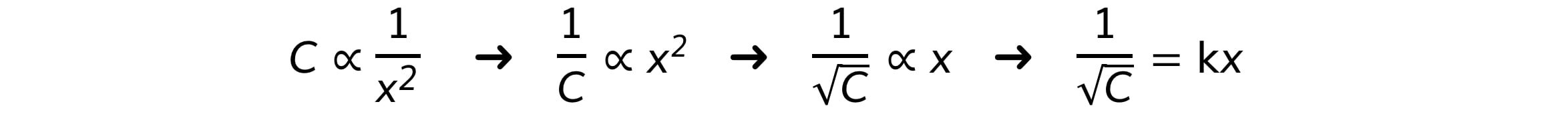
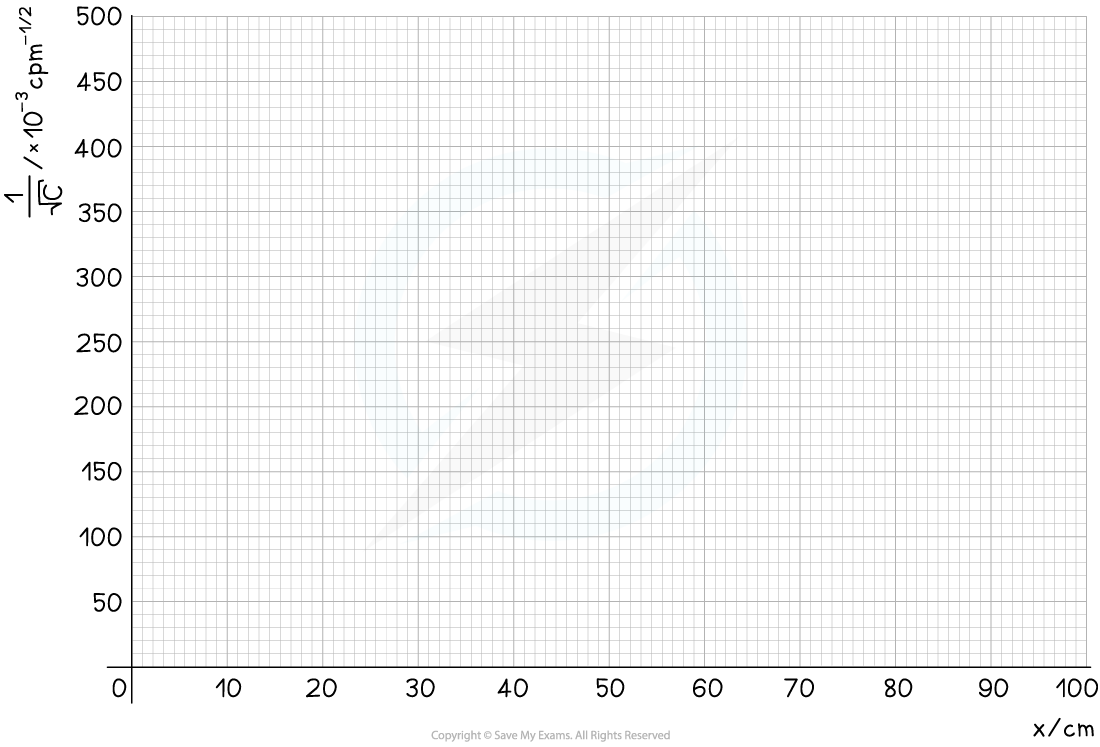
The graph provided is of the form 1/C–1/2 against x
Comparing this to the equation of a straight line, y = mx
y = 1/C–1/2 (counts min–1/2)
x = x (m)
Gradient = constant, k
If it is a straight line graph through the origin, this shows they are directly proportional, and the inverse square relationship is confirmed
Step 3: Calculate C (corrected average count rate) and C–1/2
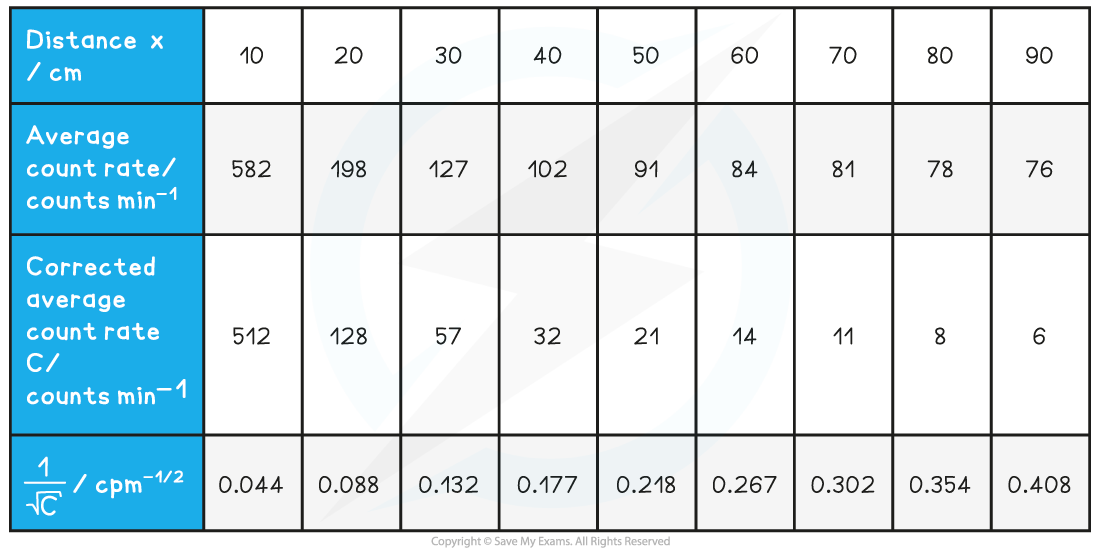
Step 4: Plot a graph of C–1/2 against x and draw a line of best fit

The graph shows C–1/2 is directly proportional to x, therefore, the data follows an inverse square law

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
