ASPhysicsCIERevision Notes9. Electricity9.1 Electric CurrentCalculating Electric Current & Charge

Syllabus Edition

First teaching 2023

First exams 2025

|

Calculating Electric Current & Charge (CIE AS Physics)

Revision Note

Test yourself
Katie M

Author

Katie M

Last updated

Calculating electric charge

  • Current can also be defined as the charge passing through a circuit per unit time
  • Electric charge is measured in units of coulombs (C)
  • Charge, current and time are related by the following equation:

Q = It 

  • Where:
    • Q = charge (C)
    • I = current (A)
    • t = time (s)

Worked example

When will 8 mA of current pass through an electrical circuit?

A.     When 1 J of energy is used by 1 C of charge

B.     When a charge of 4 C passes in 500 s

C.     When a charge of 8 C passes in 100 s

D.     When a charge of 1 C passes in 8 s

Answer: B

Step 1: Write out the equation relating current, charge and time

Q space equals space I t

I space equals fraction numerator space Q over denominator t end fraction

Step 2: Rule out any obviously incorrect options

  • Option A does not contain time, so can be ruled out

Step 3: Try the rest of the options to determine the correct answer

  • Consider option B:

I = 4 ÷ 500 = 8 × 10–3 = 8 mA

  • Consider option C:

I = 8 ÷ 100 = 80 × 10–3 = 80 mA

  • Consider option D:

I = 1 ÷ 8 = 125 × 10–3 = 125 mA

  • Therefore, the correct answer is B

Examiner Tip

Although electric charge can be positive or negative, since the conventional direction of current is the flow of positive charge the current should always be a positive value for your exam answers.

Calculating current in a current carrying conductor

  • In a conductor, current is due to the movement of charge carriers
  • These charge carriers can be negative or positive; however, the conventional current is always taken to be the flow of positive charge from the positive terminal toward the negative terminal
  • In conductors, the charge carrier is usually free electrons
  • In the image below, the conventional current in each conductor flows from right to left but the charge carriers move in the opposite direction, as shown by the direction of the drift speed v
    • In diagram A, the drift speed refers to the speed of the positive charge as if it were flowing through the conductor
    • In diagram B, the drift speed refers to the speed of the negative charge carriers actually flowing through the conductor
    • The effect is the same, which is why the model of positive charge flow works, despite it not being accurate

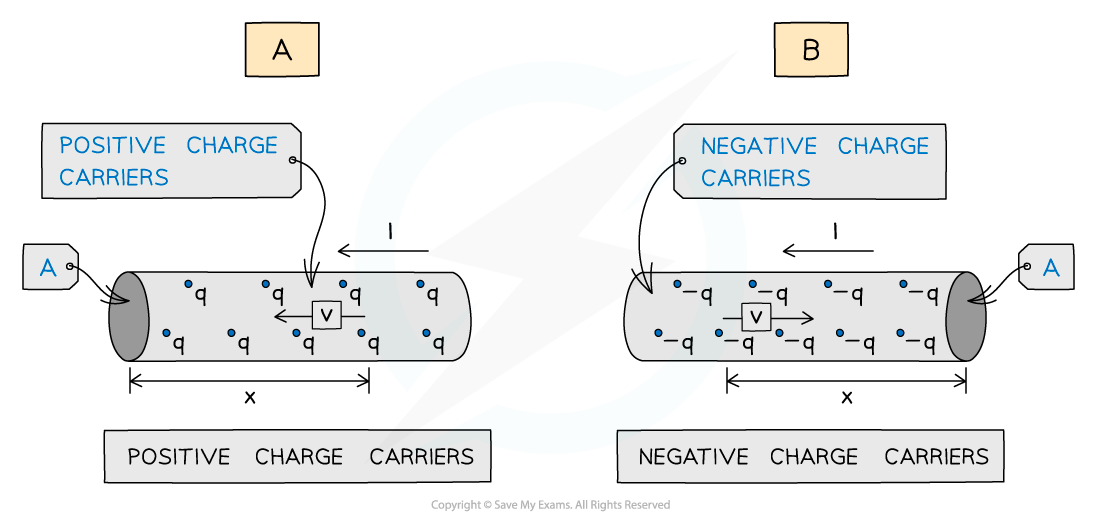
Current in a current carrying conductorCharge carriers diagram, downloadable AS & A Level Physics revision notes

The charge carriers move in opposite directions, as shown by the direction of the drift speed v.

  • The drift speed is the average speed of the charge carriers travelling through the conductor
  • This value is quite slow (only about a cm per s)
  • However, since the number density of charge carriers is so large, current is seen to flow instantaneously
  • The current can be expressed in terms of the number density (number of charge carriers per unit volume) n, the cross-sectional area A, the drift speed v and the charge of the charge carriers q

I = Anvq

    • I = current (A)
    • A = cross-sectional area (m2)
    • n = number density of charge carriers (m-3)
    • v = average drift speed of charge carriers (ms-1)
    • q = charge of each charge carrier (C)
  • The same equation is used whether the charge carriers are positive or negative

Worked example

A copper wire has 9.2 × 1028 free electrons m-3. The wire has a current of 3.5 A and a cross-sectional area of 1.5 mm2.

Calculate the average drift speed of the electrons.

Answer:

Step 1: List the known quantities

  • Number density of charge carriers, n space equals space 9.2 cross times 10 to the power of 28 space straight m to the power of negative 3 end exponent
  • Current, I space equals space 3.5 space straight A
  • Cross-sectional area, A space equals space 1.5 space mm squared space equals space 1.5 cross times 10 to the power of negative 6 end exponent space straight m squared
  • Charge on an electron, q space equals space 1.60 cross times 10 to the power of negative 19 end exponent space straight C

Step 2: State the current in a conductor equation

I space equals space A n v q

Step 3: Rearrange for drift speed v

v space equals fraction numerator space I over denominator A n q end fraction

Step 4: Substitute in values

v space equals space fraction numerator 3.5 over denominator open parentheses 1.5 cross times 10 to the power of negative 6 end exponent close parentheses open parentheses 9.2 cross times 10 to the power of 28 close parentheses open parentheses 1.60 cross times 10 to the power of negative 19 end exponent close parentheses end fraction space

v space equals space 0.16 cross times 10 to the power of negative 3 end exponent space ms to the power of negative 1 end exponent space open parentheses 2 space straight s. straight f close parentheses

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourselfNext topic

    Did this page help you?

    Katie M

    Author: Katie M

    Expertise: Physics

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.