Wavelength of Stationary Waves

Stationary waves have different wave patterns depending on the frequency of the vibration and the situation in which they are created

Two fixed ends

When a stationary wave, such as a vibrating string, is fixed at both ends, the simplest wave pattern is a single loop made up of two nodes and an antinode
- This is called the fundamental mode of vibration or the first harmonic
The particular frequencies (i.e. resonant frequencies) of standing waves possible in the string depend on its length L and its speed v
As you increase the frequency, the higher harmonics begin to appear
- The frequencies can be calculated from the string length and wave equation

For a string of length L, the wavelength of the lowest harmonic is 2L
- This is because there is only one loop of the stationary wave, which is a half wavelength
$λ_{n} = \frac{2 L}{n}$

$λ_{1} = \frac{2 L}{1} = 2 L$

The second harmonic has three nodes and two antinodes
- So the wavelength is equal to the length of the string

$λ_{2} = \frac{2 L}{2} = L$

The third harmonic has four nodes and three antinodes

$λ_{3} = \frac{2 L}{3}$

The nth harmonic has n antinodes and n + 1 nodes
The nth wavelength has a wavelength of $\frac{2 L}{n}$

The wavelengths and frequencies of the first three harmonics can be summarised as follows:

Wavelength and frequencies of different harmonics

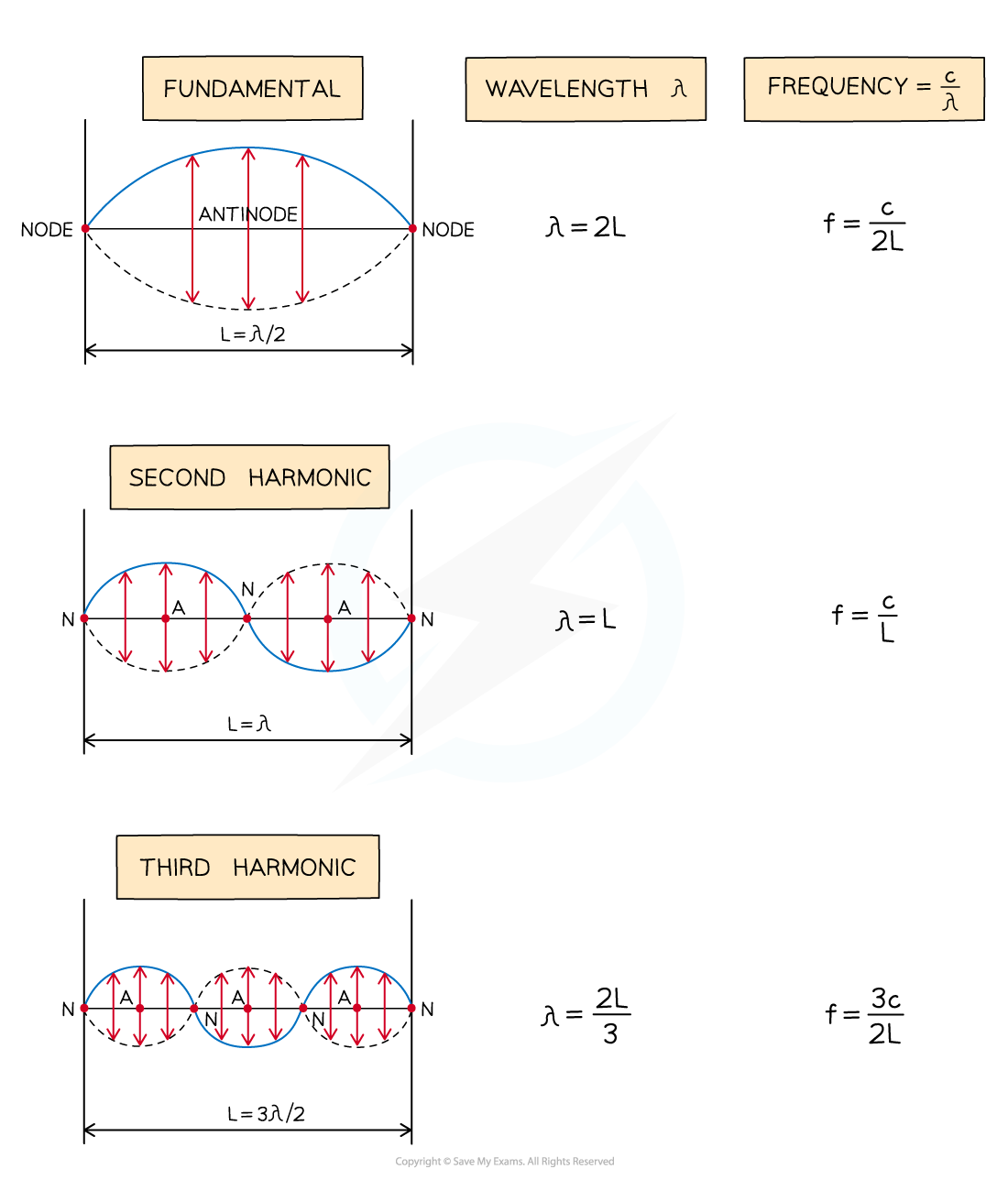
Fixed end wavelengths and harmonics, downloadable AS & A Level Physics revision notes

Diagram showing the first three modes of vibration of a stretched string with corresponding frequencies

One or two open ends in an air column

When a stationary wave is formed in an air column with one or two open ends, slightly different wave patterns are seen in each

Harmonics in an air column

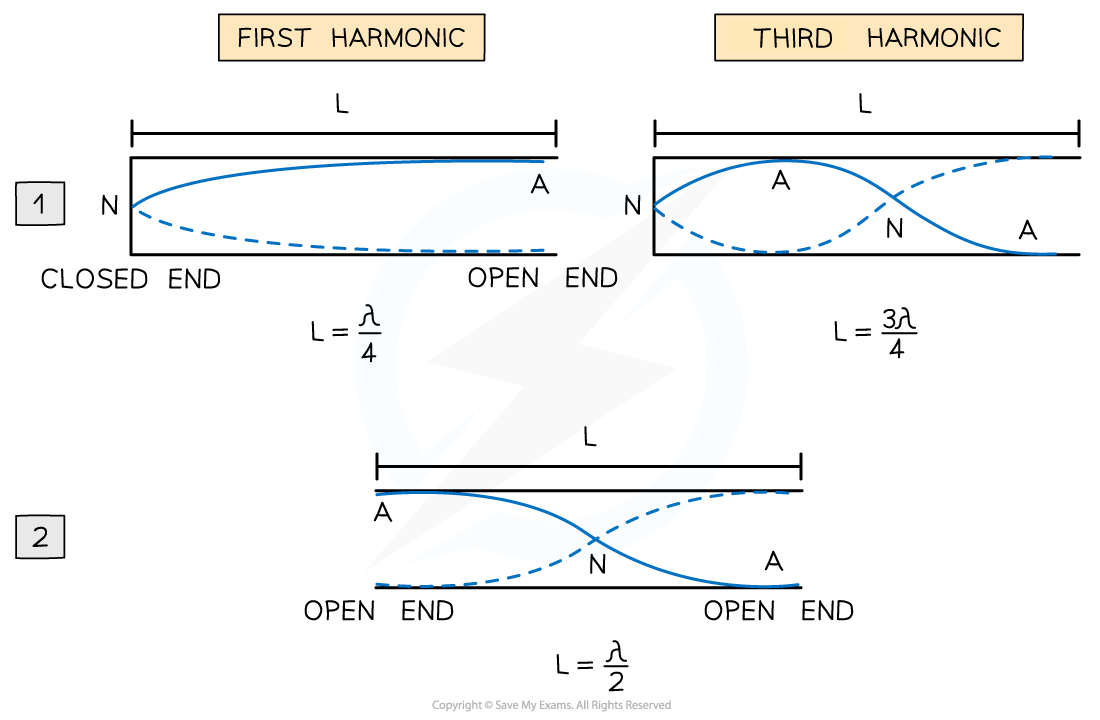
3-2-3-closed-and-open-ends

Diagram showing modes of vibration in pipes with one end closed and the other open or both ends open

Image 1 shows stationary waves in a column which is closed at one end
- At the closed end, a node forms
- At the open end, an antinode forms

Therefore, the fundamental mode is made up of a quarter wavelength with one node and one antinode
- Every harmonic after that adds on an extra node or antinode
- Hence, only odd harmonics form

Image 2 shows stationary waves in a column which is open at both ends
- An antinode forms at each open end

Therefore, the fundamental mode is made up of a half wavelength with one node and two antinodes
- Every harmonic after that adds on an extra node and an antinode
- Hence, odd and even harmonics can form

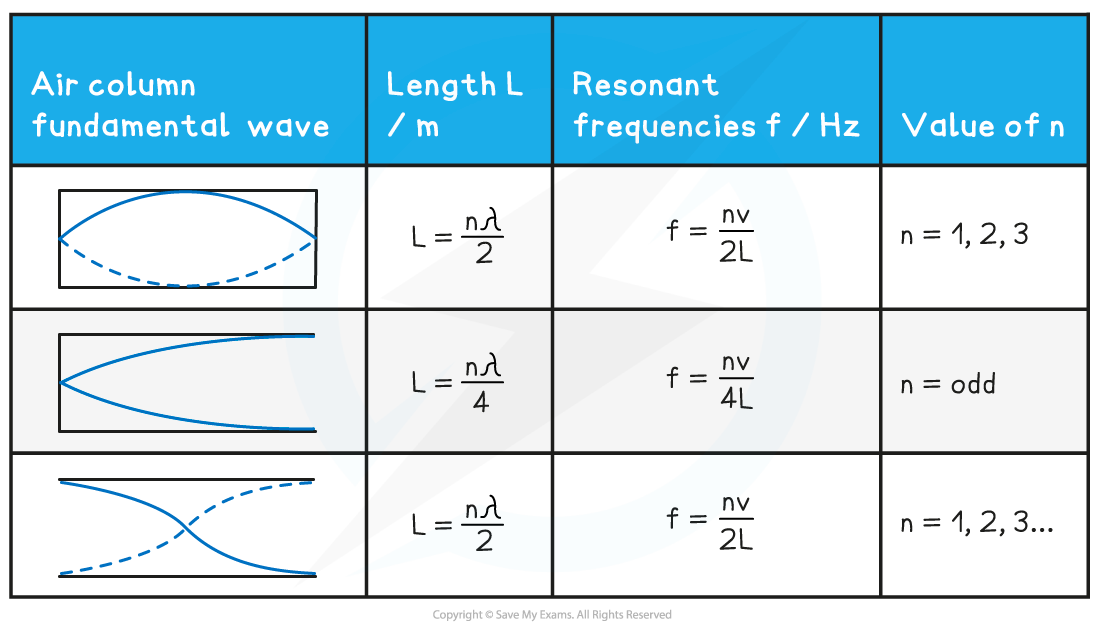
In summary, a column length L for a wave with wavelength λ and resonant frequency f for stationary waves to appear is as follows:

Air Column Length & Frequencies Summary Table

new-8-1-4-table-of-length

Worked example

A standing wave is set up in a column of length L when a loudspeaker placed at one end emits a sound wave of frequency f. The column is closed at the other end. The speed of sound is 340 m s⁻¹.

For a column of length 7.5 m, what is the wavelength of the second lowest note produced?

Answer:

Step 1: Determine the positions of the nodes and antinodes

One end of the column is closed, and the loudspeaker represents an open end
Hence, an antinode forms at the loudspeaker (open end) and a node forms at the closed end
The fundamental frequency represents the lowest note - this would be 1 node and 1 antinode
So, the second-lowest note must have 2 nodes and 2 antinodes

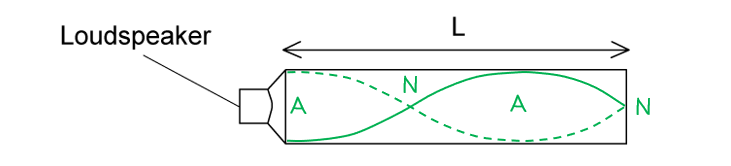
closed-and-open-ends-ma

Step 2: Write an expression for the length of the sound wave in the column

In the column, there is a quarter wavelength and a half wavelength, or $\frac{3}{4} λ$
Therefore the length of the column is:

$L = \frac{3 λ}{4}$

Note: for a column with an open and closed end, $L = \frac{n λ}{4}$ , this would represent the third harmonic (n = 3)

Step 3: Determine the wavelength of the second lowest note

$λ = \frac{4 L}{3} = \frac{4 \times 7.5}{3} = 10 m$

Examiner Tip

The fundamental counts as the first harmonic or n = 1 and is the lowest frequency with half or quarter of a wavelength. A full wavelength with both ends open or both ends closed is the second harmonic. Make sure to match the correct wavelength with the harmonic asked for in the question!

Wavelength of Stationary Waves (CIE AS Physics)

Revision Note