Revision NotesExam QuestionsPast Papers
ASPhysicsCambridge (CIE)Revision Notes7. WavesPolarisationPolarisation

Polarisation (Cambridge (CIE) AS Physics)

Revision Note

Katie M

Written by: Katie M

Reviewed by: Caroline Carroll

Updated on

Polarisation

Polarisation of transverse waves

  • Transverse waves are waves that oscillate with their displacement perpendicular to their direction of travel

    • These oscillations can happen in any plane perpendicular to the propagation direction

  • An electromagnetic wave is an example of a transverse wave that oscillates in more than one plane

    • A magnetic field oscillates on one plane

    • An electric field oscillates on a different plane

    • Both planes are at right angles to each other and to the direction of wave motion

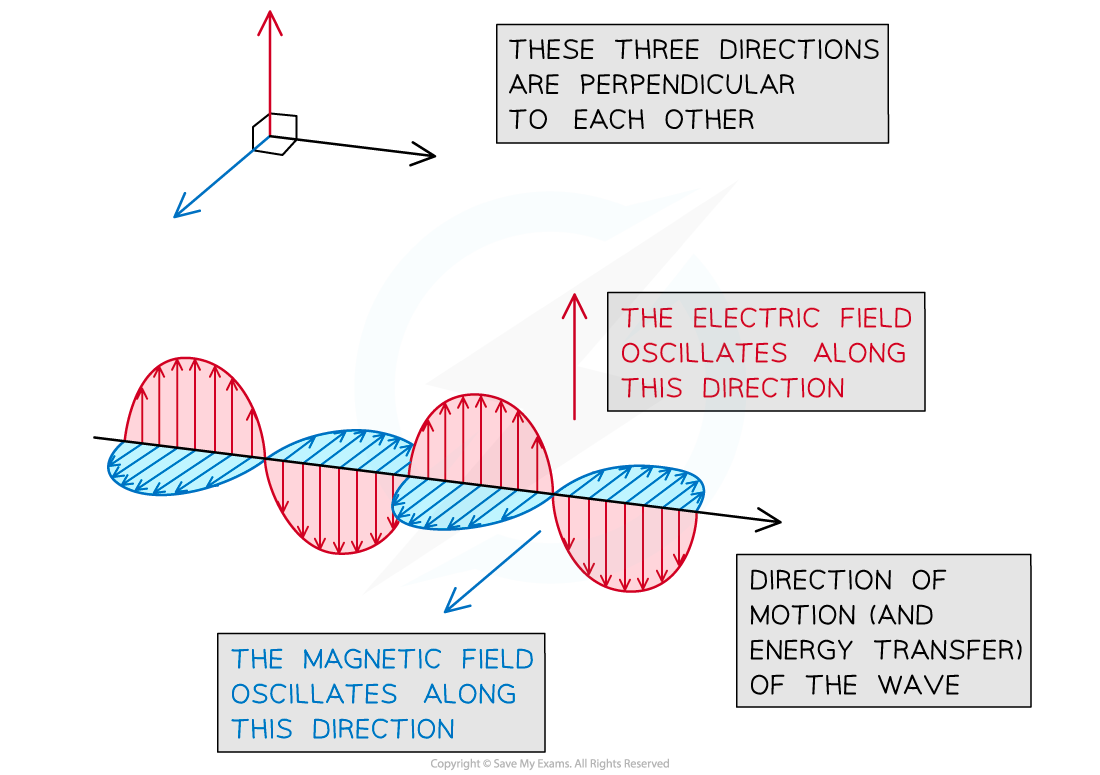
4-2-3-oscillating-electric-and-magnetic-fields_sl-physics-rn

An electromagnetic wave is generated by the combined oscillation of an electric and a magnetic field

  • When transverse waves are polarised

    • vibrations are restricted to one plane of oscillation

    • vibrations are still perpendicular to the direction of propagation / energy transfer

  • The difference between unpolarised and polarised waves are shown in the diagram below

    • The blue arrows represent the direction of the plane of oscillation of the transverse wave

  • An unpolarised wave oscillates in many planes of oscillation

  • A vertically polarised wave oscillates only in the vertical plane

  • A horizontally polarised wave oscillates only in the horizontal plane

Different planes of polarisation

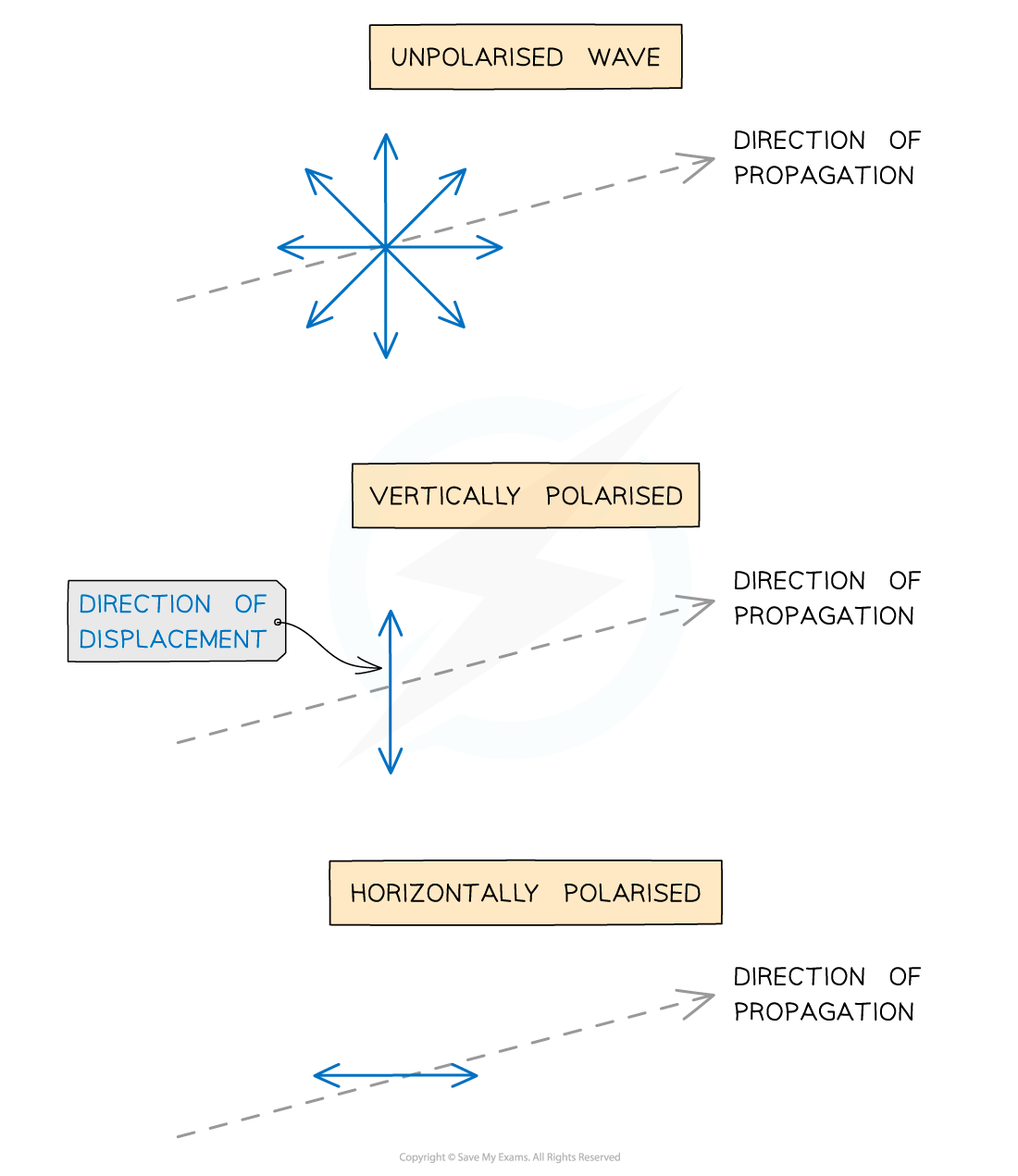
Polarised waves diagram, downloadable AS & A Level Physics revision notes

Diagram showing the displacement of unpolarised and polarised transverse waves

Polarising filters

  • Waves can be polarised by passing through a polariser or polarising filter. 

    • Polarisers only allow oscillations in a certain plane to be transmitted through the filter

  • A polariser is an optical layer or lens that consists of many parallel tiny slits

    • A polariser only allows waves vibrating parallel to the direction of these slits to pass through

    • Waves that are not orientated in the correct plane are blocked by the filter and do not pass through

 Action of a polarising filter

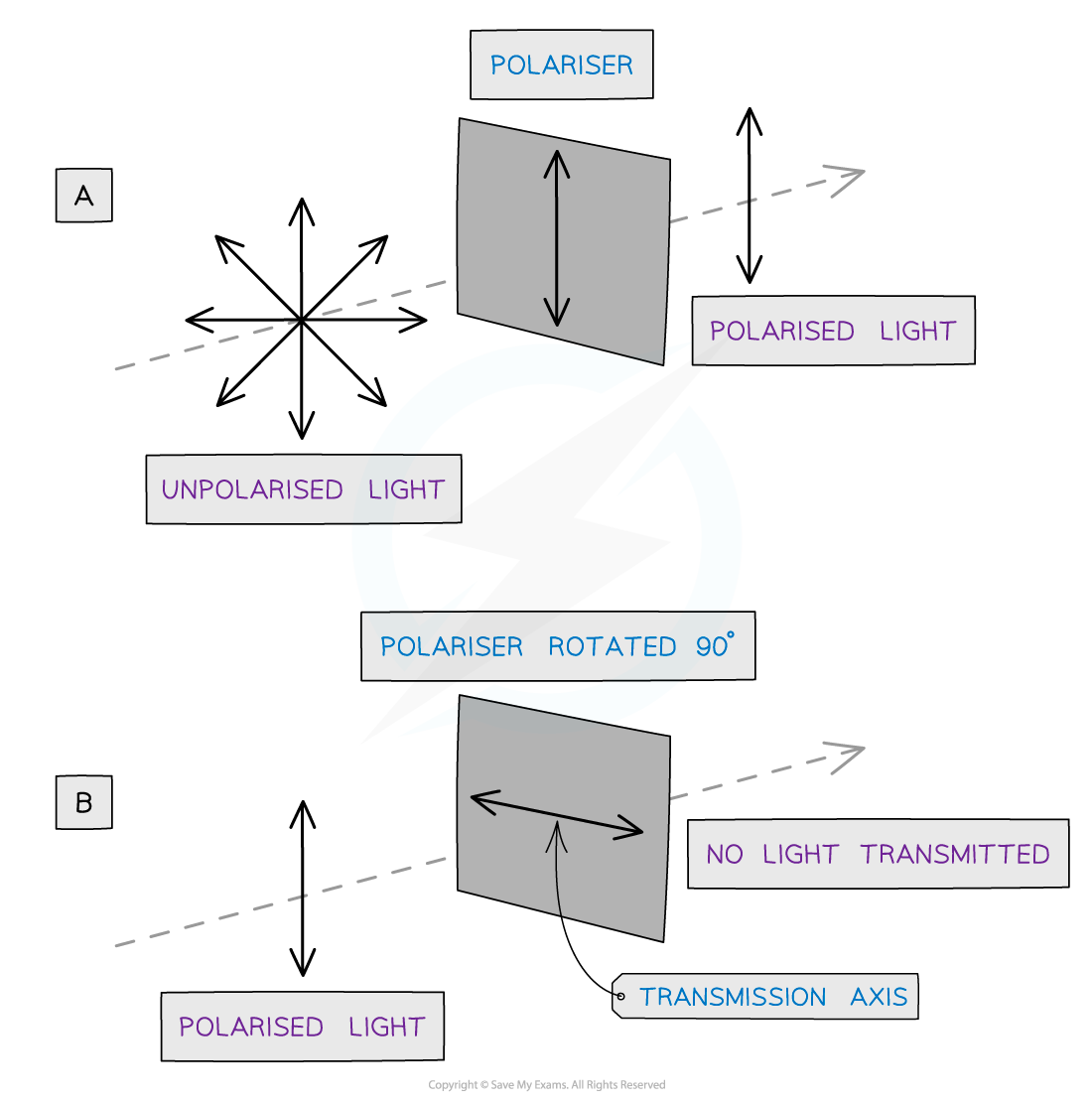
Waves through a polariser, downloadable AS & A Level Physics revision notes

Diagram showing an unpolarised and polarised wave travelling through polarisers

  • Only unpolarised waves can be polarised 

    • This is shown in diagram A

    • When a polarised wave passes through a filter with a transmission axis perpendicular to the wave (diagram B), none of the wave will pass through

Polaroid sunglasses

  • Polaroid sunglasses are an example of a polarisation

  • Polaroid sunglasses contain lenses with polarising filters with transmission axes that are vertically oriented

    • This means the glasses do not allow any horizontally polarised light to pass through

Polaroid sunglasses

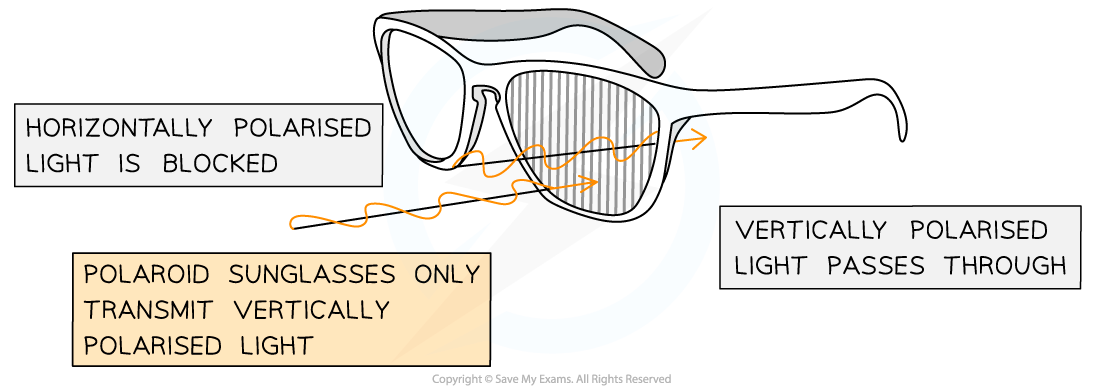
Polaroid Sunglasses (1), downloadable AS & A Level Physics revision notes

Polaroid sunglasses contain vertically oriented polarising filters which block out any horizontally polarised light

Worked Example

The following are statements about waves.

Which statement below describes a situation in which polarisation should happen?

A. Radio waves pass through a metal grid

B. Surface water waves are diffracted

C. Sound waves are reflected

D. Ultrasound waves pass through a metal grid

Answer: A

  • Polarisation only occurs for transverse waves, therefore, C and D can be ruled out as sound and ultrasound are both longitudinal waves

  • Waves are not polarised when diffracted, hence we can also rule out option B

  • Radio waves are transverse waves - they can be polarised by a metal grid so only the waves that fit through the grid will be transmitted, therefore, A is correct

Malus's law

Intensity of polarised electromagnetic waves

  • The intensity of electromagnetic waves is reduced as a result of polarisation

  • If unpolarised electromagnetic waves of intensity I0 pass through a polariser, the intensity of the transmitted polarised waves falls by a half

    •  I space equals space I subscript 0 over 2 is known as the half rule

Intensity of polarised and unpolarised light

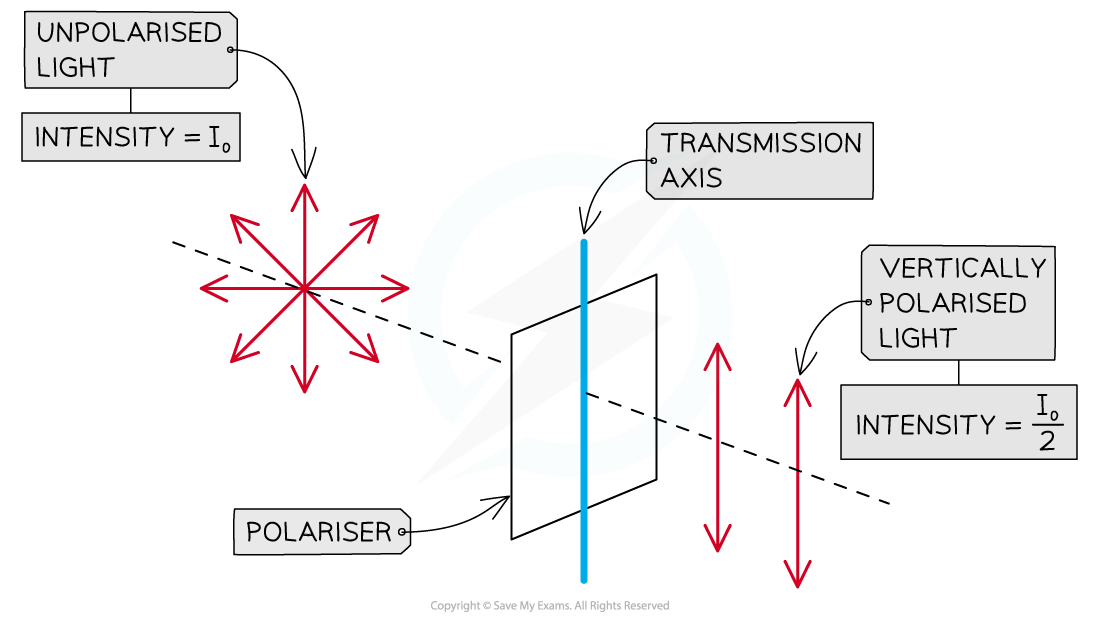
4-3-5-unpolarised-vs--polarised-light-intensity_sl-physics-rn

The intensity of polarised light transmitted by a polariser is half the intensity of the unpolarised light incident on it

Intensity of analysed electromagnetic waves

  • A second polarising filter placed after the first is known as an analyser 

Intensity of waves when polariser and analyser have the same orientation

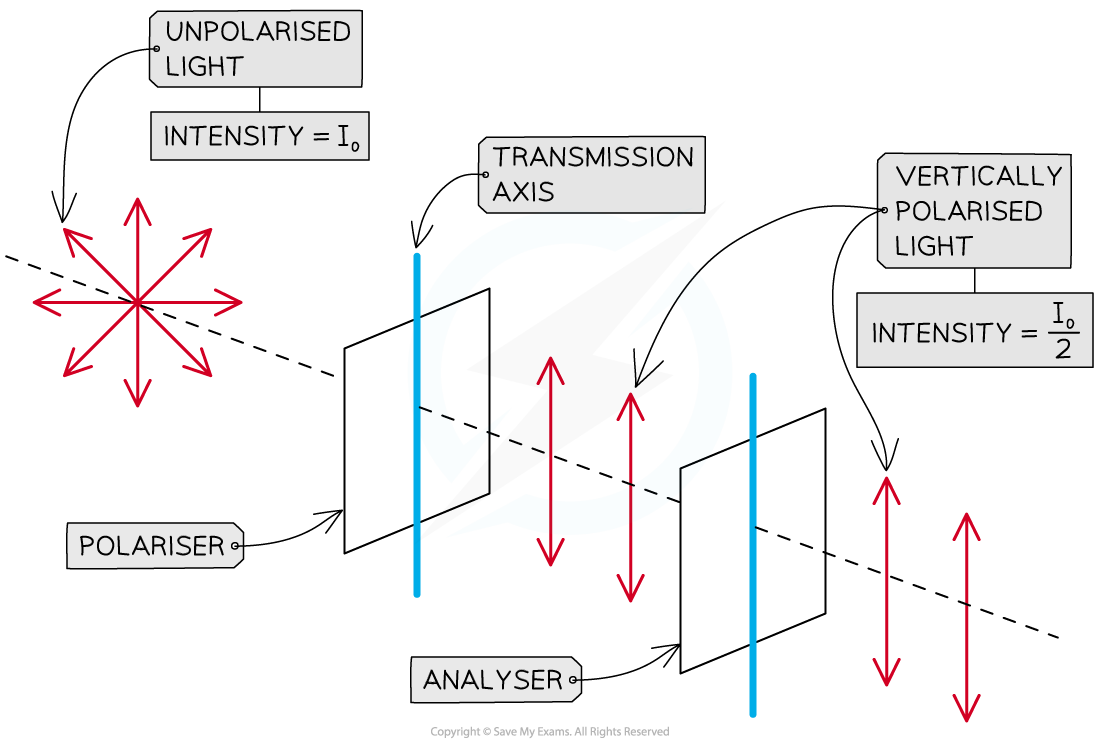
4-3-5-polariser-and-analyser-same-orientation_sl-physics-rn

When the polariser and the analyser have the same orientation (i.e. parallel transmission axes), the intensity of analysed light is the same as the intensity of polarised light

Malus's law

  • Malus's law states that if the analyser is rotated by an angle θ  with respect to the polariser, the intensity of the waves transmitted by the analyser is given by the equation

 I space equals space I subscript 0 cos squared open parentheses theta close parentheses

  • Where

    • I is intensity of transmitted light in W m−2

    • I0 is maximum intensity (same units)

  • If the polariser and the analyser have the same orientation, electromagnetic waves transmitted by the analyser have the same intensity as waves that are incident upon it, since cos(0) = 1

    • If vertically polarised electromagnetic waves with intensity I subscript 0 over 2 are incident on an analyser with a vertical transmission axis, all of the waves will be transmitted through the analyser 

    • The intensity between the polariser and the analyser will not decrease 

  • If the analyser is rotated by 90° with respect to the polariser (θ = 90°), the intensity of the light transmitted by the analyser will be zero, since cos(90°) = 0

    • If vertically polarised light is incident on an analyser with a horizontal transmission axis, none of the light will be transmitted through the analyser

    • In this instance, all the waves will be absorbed

Table of transmission depending on polariser orientation

Angle of transmission axis, θ / degrees

Direction of transmission axis

cos2θ

Transmitted intensity / W m−2

Maximum or minimum light intensity transmitted

0

Vertical

1

I0

Max

180

Vertical

1

I0

Max

90

Horizontal

0

0

Min

270

Horizontal

0

0

Min

Worked Example

Unpolarised light is incident on a polariser.

The light transmitted by the first polariser is then incident on a second polariser.

The polarising (or transmission) axis of the second polariser is 30° to that of the first. The intensity incident on the first polariser is I.

What is the intensity emerging from the second polariser?

A. 0.75 I         

B. 0.38 I         

C. 0.87 I         

D. 0.43 I

Answer: B

Step 1: Apply the half rule:

  • When light passes through the first polariser, half its intensity is lost

I subscript 1 space equals space 1 half I

Step 2: Use Malus's law:

  • The angle of the transmission axis is 30°

  • In this case, I0 in Malus's equation is I1 here, because the light has already passed through the first polariser

I subscript 2 space equals space I subscript 1 cos squared open parentheses theta close parentheses space equals space 1 half I space cos squared open parentheses 30 degree close parentheses space equals space 1 half I space cross times space 3 over 4

I subscript 2 space equals space 3 over 8 I space equals space 0.375 space I

  • To 2 significant figures, this is option B

Examiner Tips and Tricks

Remember when using Malus’s law to square the cosine of the angle (cos2 θ)

Remember that the unpolarised light coming through will always halve in intensity when it becomes polarised through an polariser. Only then should you use Malus' law to find the intensity of the light after it has passed through the analyser. Therefore, the I and I0 in Malus' law are the intensities of light that are already polarised.

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Electromagnetic SpectrumNext:The Principle of Superposition
    Author
    Reviewer
    Katie M

    Author: Katie M

    Expertise: Physics

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.

    Caroline Carroll

    Author: Caroline Carroll

    Expertise: Physics Subject Lead

    Caroline graduated from the University of Nottingham with a degree in Chemistry and Molecular Physics. She spent several years working as an Industrial Chemist in the automotive industry before retraining to teach. Caroline has over 12 years of experience teaching GCSE and A-level chemistry and physics. She is passionate about creating high-quality resources to help students achieve their full potential.