Revision NotesExam QuestionsPast Papers
ASPhysicsCIERevision Notes7. Waves7.1 Progressive WavesWave Intensity

Wave Intensity (CIE AS Physics)

Revision Note

Katie M

Author

Katie M

Last updated

Wave intensity

  • Progressive waves transfer energy
  • The amount of energy passing through a unit area per unit time is the intensity of the wave
  • Therefore, the intensity is defined as power per unit area

I space equals space P over A

  • Where
    • I is intensity in W m−2
    • P is power in W
    • A is area in m2

  • The area the wave passes through is perpendicular to the direction of its velocity
  • The intensity of a progressive wave is also proportional to its amplitude squared and frequency squared

I space proportional to space A squared

I space proportional to space f squared

  • Where
    • A is amplitude in m
    • f is frequency in Hz
  •  Recall that ∝ means "proportional to"

  • This means that if the frequency or the amplitude is doubled, the intensity increases by a factor of 4 (22)

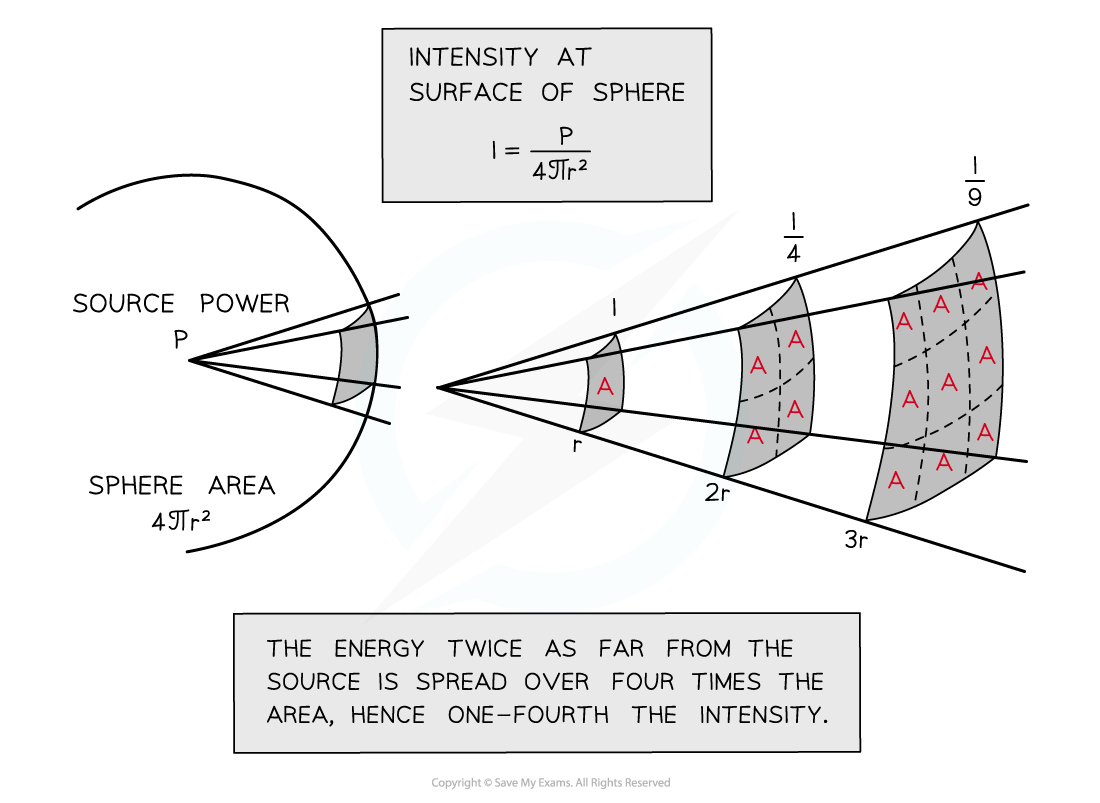
Spherical waves

  • A spherical wave is a wave from a point source which spreads out equally in all directions
  • The area the wave passes through is the surface area of a sphere: 4πr2
  • As the wave travels further from the source, the energy it carries passes through increasingly larger areas as shown in the diagram below:

Inverse square law for intensity

Intensity of a spherical wave, downloadable AS & A Level Physics revision notes

Intensity is proportional to the amplitude squared

 

  • Assuming none of the wave energy is absorbed, the intensity I decreases with increasing distance from the source
  • The inverse square law states that

 I space proportional to 1 over r squared

    • The inverse square law means when the source is twice as far away, the intensity is 4 times smaller

Worked example

The intensity of a progressive wave is proportional to the square of the amplitude of the wave. It is also proportional to the square of the frequency. The variation with time t of displacement x of particles when two progressive waves Q and P pass separately through a medium, are shown on the graphs.

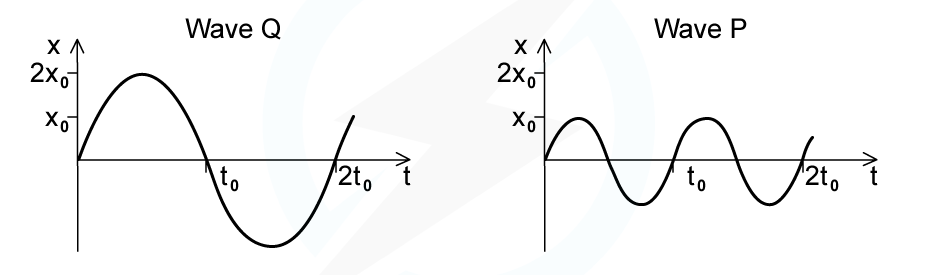
The intensity of wave Q is I0.What is the intensity of wave P?

Answer:

Step 1: Compare waves Q and P:

  • The amplitude of wave Q is twice the amplitude of wave P
  • The frequency of wave P is double the frequency of wave Q

Step 2: Evaluate how amplitude affects the intensities:

  • Q has twice the amplitude of P 

A subscript Q over A subscript P space equals space 2

  • The ratio of amplitudes squared is equal to the ratio of intensities, because intensity and amplitude squared are proportional

A subscript Q squared over A subscript P squared space equals space 4 space equals space I subscript Q over I subscript P

I subscript Q space equals space 4 I subscript P

  • So Q's larger amplitude increases its intensity by a factor of 4

Step 3: Evaluate how frequency affects the intensities:

  • Q has half the frequency of P

f subscript Q over f subscript P space equals space 1 half

  • The ratio of frequencies squared is equal to the ratio of intensities because intensity and frequency squared are proportional

f subscript Q squared over f subscript P squared space equals space 1 fourth space equals space I subscript Q over I subscript P

I subscript Q space equals space 1 fourth I subscript P

  • So Q's lower frequency decreases its intensity by a factor of 4

Step 4: Determine the intensity of wave P in terms of I0 :

  • P has a lower amplitude which reduces its intensity by a factor of 4 compared to Q
  • However, P has a higher frequency which increases its intensity by a factor of 4 compared to Q
  • These effects cancel out, so wave P has an intensity of I0 , which is equal to that of wave Q

Examiner Tip

The key concept with intensity is that it has an inverse square relationship with distance (not a linear one). This means the energy of a wave decreases very rapidly with increasing distance

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:The Wave EquationNext:Transverse & Longitudinal Waves
    Katie M

    Author: Katie M

    Expertise: Physics

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.