Revision NotesExam QuestionsPast Papers
ASPhysicsCIERevision Notes6. Deformation of Solids6.1 Stress & StrainHooke's Law

Hooke's Law (CIE AS Physics)

Revision Note

Katie M

Author

Katie M

Last updated

Hooke's law

  • A material demonstrating elastic behaviour obeys Hooke’s Law if its extension is directly proportional to the applied force (load)
  • The Force-extension graph of an object obeying Hooke's law is a straight line through the origin 
  • This linear relationship is represented by the Hooke’s law equation

F space equals space k x

  • Where:
    • F is force applied in N
    • k is the spring constant in N m−1
    • x is the extension of the spring

The spring constant

  • k is the spring constant of the spring and is a measure of the stiffness of a spring
    • A stiffer spring will have a larger value of k

  • k is defined as the force per unit extension up to the limit of proportionality
  • The SI unit for the spring constant is N m-1
  • Rearranging the Hooke’s law equation shows the equation for the spring constant is

k space equals space F over m

  • Therefore, the spring constant k is the gradient of the linear part of a force-extension graph

Gradient of force-extension graph

Spring constant on graph, downloadable AS & A Level Physics revision notes

Spring constant is the gradient of a force vs extension graph

Worked example

A spring was stretched with increasing load.

The graph of the results is shown below.

WE - hookes law question image, downloadable AS & A Level Physics revision notes

Determine the value of the spring constant.

Answer:

Step 1: Rearrange Hooke's Law:

  • Spring constant, k, is:

k space equals space F over x

Step 2: Relate the gradient of this graph to k :

  • The y axis of this graph is length L and the x axis is load F
  • Gradient is change in y over change in x:

gradient space equals space fraction numerator straight capital delta L over denominator straight capital delta F end fraction space equals space x over F

  • The change in length is the extension x
  • Therefore:

gradient space equals space 1 over k

Step 3: Determine the gradient of the graph:

  • Choose a large section of the graph line to determine the changes in the x and y axes

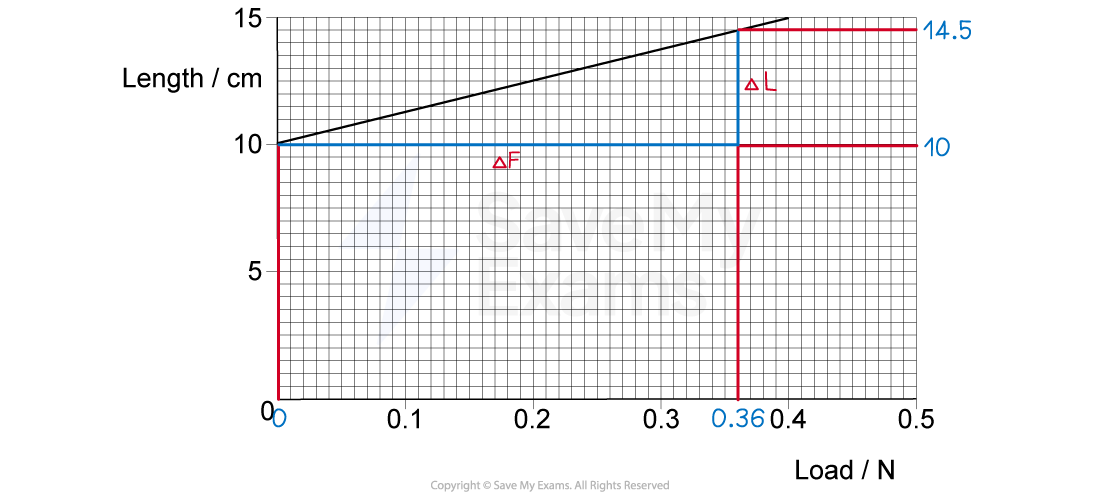
6-1-2-we-hookes-law-cie-new

  • Convert the extension from cm to m

gradient space equals space fraction numerator 0.145 space minus space 0.100 over denominator 0.36 end fraction space equals space 0.125 space straight m space straight N to the power of negative 1 end exponent

Step 4: Calculate the spring constant:

  • The spring constant is

k space equals space 1 over gradient space equals space fraction numerator 1 over denominator 0.125 end fraction space equals space 8.0 space straight N space straight m to the power of negative 1 end exponent

Examiner Tip

Double check the axes before finding the spring constant as the gradient of a force-extension graph. Exam questions often swap the load onto the x-axis and length on the y-axis. In this case, the spring constant is 1 over gradient and not the spring constant.

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Extension & CompressionNext:The Young Modulus
    Katie M

    Author: Katie M

    Expertise: Physics

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.