Efficiency | CIE AS Physics Revision Notes 2025

Efficiency of a system

The efficiency of a system is the ratio of the useful energy output from the system to the total energy input
- If a system has high efficiency, this means most of the energy transferred is useful
- If a system has low efficiency, this means most of the energy transferred is wasted
Multiplying this ratio by 100 gives the efficiency as a percentage
The efficiency is calculated using the equation:

$efficiency = \frac{useful energy output}{total energy input} \times 100 %$

Efficiency can also be written in terms of power (the energy transferred per second):

$efficiency = \frac{useful power output}{total power input}$

Worked example

An electric motor has an input power, P_in, useful output power, P_out, power lost P_lost, and an efficiency η.

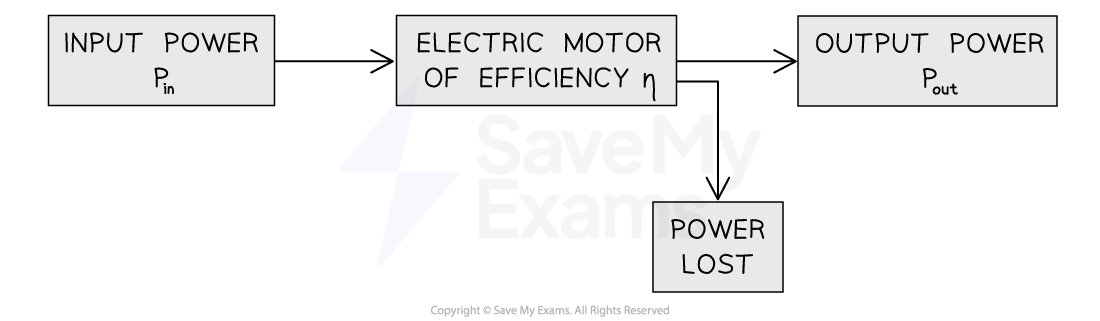
5-1-3-we-efficiency-of-a-system-question-cie-new

What is the output power of the motor?

A: $\frac{η}{P_{i n}}$ B: $\frac{- η P_{l o s t}}{η - 1}$ C: $η P_{l o s t}$ D: $- η P_{l o s t} (η - 1)$

Answer: B

Step 1: State the efficiency equation

$efficiency = \frac{useful power output}{total power input}$

Step 2: Substitute the terms given in the question

$η = \frac{P_{o u t}}{P_{i n}} = \frac{P_{o u t}}{P_{o u t} + P_{l o s t}}$

Step 3: Manipulate the equation

Multiply by P_out + P_lost on both sides

$η (p_{o u t} + p_{l o s t}) = P_{o u t}$

Expand the brackets

$η P_{o u t} + η P_{l o s t} = P_{o u t}$

Minus P_out from both sides
- It is helpful to first minus ηP_lost

$η P_{o u t} = P_{o u t} - η P_{l o s t}$

$η P_{o u t} - P_{o u t} = - η P_{l o s t}$

Factor out P_out

$P_{o u t} (η - 1) = - η P_{l o s t}$

Divide by η − 1

$P_{o u t} = \frac{- η P_{l o s t}}{(η - 1)}$

Examiner Tip

Efficiency can be in a ratio or percentage format. If the question asks for an efficiency as a ratio, give your answer as a fraction or decimal. If the answer is required as a percentage, remember to multiply the ratio by 100 to convert it, e.g. Ratio = 0.25, Percentage = 0.25 × 100 = 25 %

Solving problems involving efficiency

Efficiency calculations are often part of a larger multi-step problem
Since efficiency deals with energy and power, questions will often involve energy or power calculations

Worked example

The diagram shows a pump called a hydraulic ram.

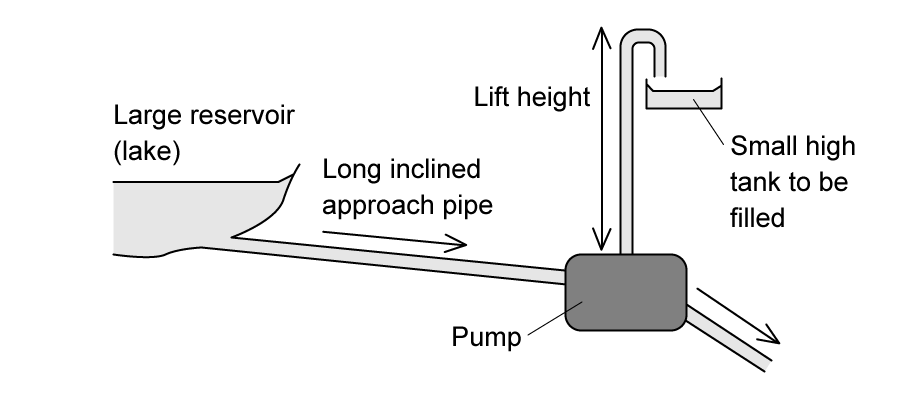
In one such pump, the long approach pipe holds 700 kg of water. A valve shuts when the speed of this water reaches 3.5 m s^-1. The kinetic energy of this water is used to lift a small quantity of water by a height of 12m. The efficiency of the pump is 20%.

Which mass of water could be lifted 12 m?

A. 6.2 kg B. 4.6 kg C. 7.3 kg D. 0.24 kg

Answer: C

Step 1: List the known quantities

Mass of water in approach pipe = 700 kg
Speed of water in approach pipe, v = 3.5 m s^-1
Height of lifted water, h = 12 m

Step 2: Consider the energy transfer taking place

Energy is transferred from the kinetic store of the water to its gravitational potential store

Step 3: Consider the efficiency of the energy transfer

The transfer is 20% efficient
Therefore, 20% of the kinetic input energy is output as gravitational potential energy

$0.2 E_{k} = E_{p}$

$0.2 \times \frac{1}{2} m v^{2} = m g h$

Step 4: Calculate the mass of water lifted water

$0.2 \times 0.5 \times 700 \times {(3.5)}^{2} = m \times 9.81 \times 12$

$857.5 = m \times 117.72$

$m = \frac{857.5}{117.72}$

$m = 7.3 kg$

Examiner Tip

Equations for kinetic and potential energies are important for these types of questions. Also, familiarise yourself with the different equations for power depending on what quantities are given.

Efficiency (CIE AS Physics)

Revision Note

Efficiency of a system

Worked example

Examiner Tip

Solving problems involving efficiency

Worked example

Examiner Tip

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Leander