Derivation of ∆p = ρg∆h (Cambridge (CIE) AS Physics)

Derivation of ∆p = ρg∆h

• Hydrostatic pressure is the pressure at any given point within a fluid, that is exerted by the weight of the fluid above that point 

• If the fluid is at rest, then all the points within the fluid are in equilibrium

• Therefore, the pressure acts in all directions at each point

Pressure on a point in a fluid

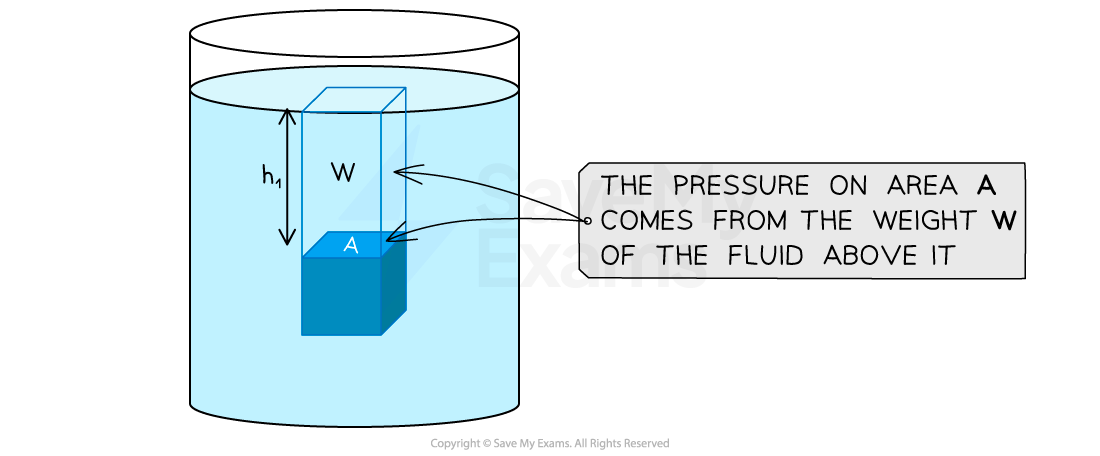
The hydrostatic pressure on area A is due to the weight, W, of the volume of fluid above it

• The weight, W, of the fluid above area A is given by:

• Using the density equation, mass can be given as:

• Substituting this expression for mass into the weight equation gives:

• Therefore, the pressure exerted on area A can be given as:

• Within the volume of the cube V, there is a change in pressure between the top and bottom surfaces

Change in pressure through a volume of fluid

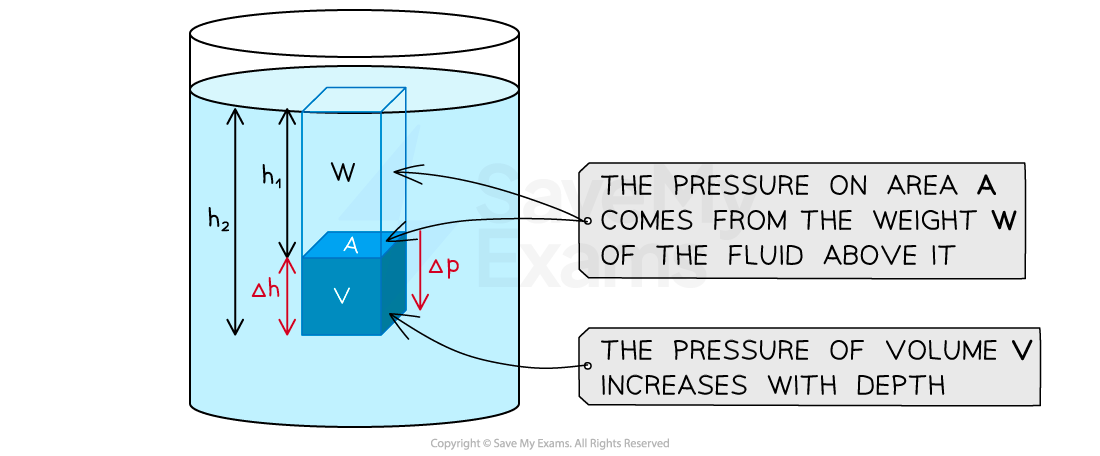
The pressure at the bottom of the cube with volume V is greater than the area A at the top of the cube, because there is an increasing amount of fluid above, which increases the force of weight W acting upon it

• The change in pressure can be found by considering the change in height of the volume of fluid above the lower surface

• This gives the equation for hydrostatic pressure:

• Where:

  • Δp = change in pressure in pascals (Pa)

  • ρ (Greek letter rho) = density of fluid in kilograms per metre cubed (kg m^-3)

  • Δh = change in height in metres (m)

  • g = gravitational field strength in newtons per kg (N kg^-1)

Using the equation for hydrostatic pressure

• When an object is immersed in a liquid, the liquid will exert a pressure which acts in all directions, squeezing the object

• The size of this pressure depends upon:

  • The density, ρ, of the liquid

  • The depth, h, of the object

  • The gravitational field strength, g

• The total pressure acting on the object considers both the weight of the fluid above the object, and the weight of the air above the object

• When asked about the total pressure, the atmospheric pressure must also be included

Total pressure = Hydrostatic pressure + Atmospheric pressure

• Atmospheric pressure (also known as barometric pressure) is 101 325 Pa

U-tube manometer

• A manometer is an instrument to measure pressure and density of two liquids

A U-tube manometer

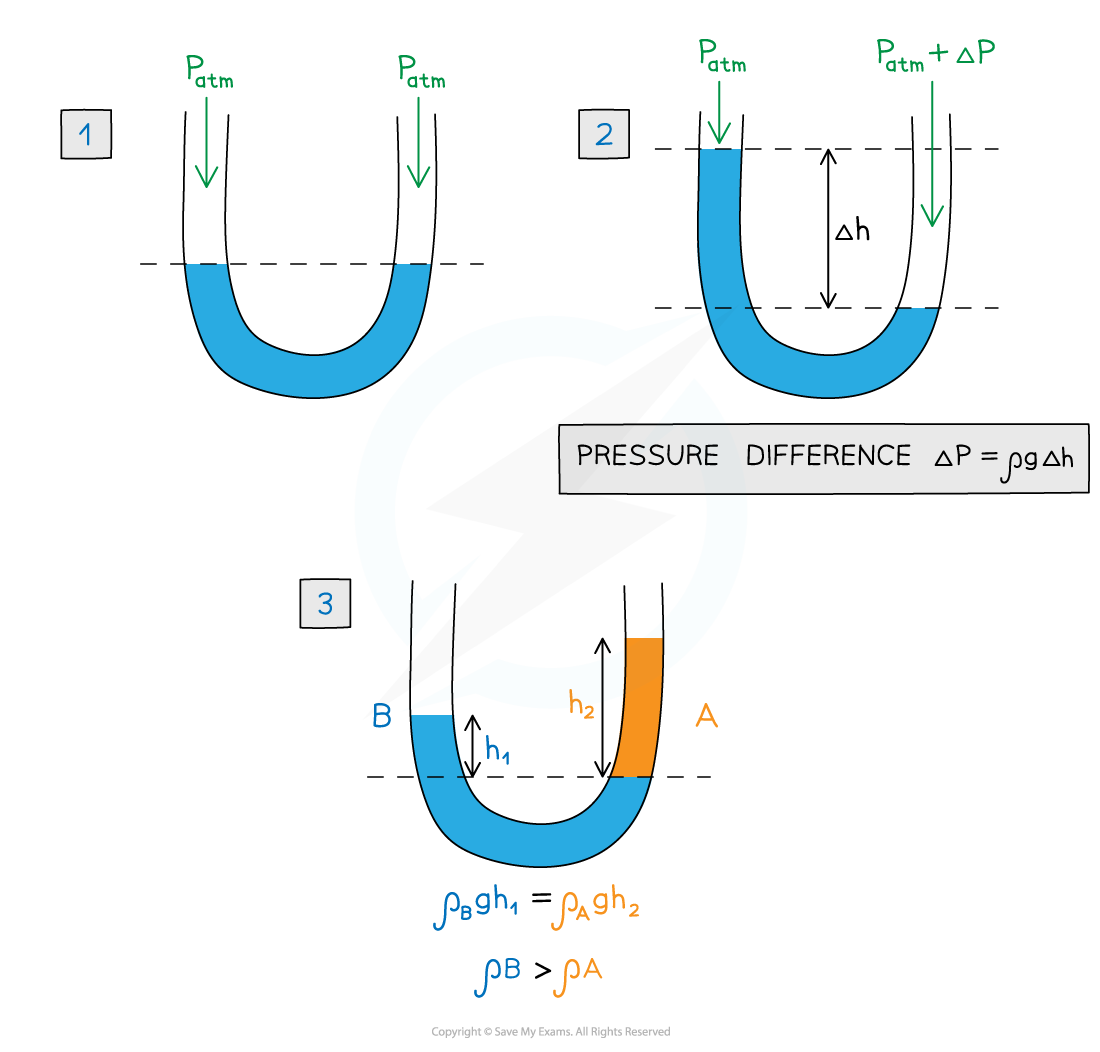
A U-tube manometer shows changes in pressure as the liquid moves in the tube

• In Figure 1: The level of liquid is equal because the atmospheric pressure (P_atm) is the same

• In Figure 2: If the pressure on one side rises, the liquid will be forced down making the liquid in the other limb rise. The difference between the two levels gives the pressure difference between the two ends of the tube

• In Figure 3: The U-tube now has two different liquids. The density of the blue one is greater than that of the orange one. The pressure at each point is due to the atmospheric pressure plus the weight of the liquid above it