Revision NotesExam QuestionsPast Papers
ASPhysicsCambridge (CIE)Revision Notes4. Forces, Density & PressureDensity & PressureArchimedes' Principle

Archimedes' Principle (Cambridge (CIE) AS Physics)

Revision Note

Leander Oates

Written by: Leander Oates

Reviewed by: Caroline Carroll

Updated on

Archimedes' principle

  • Archimedes’ principle states that:

    An object submerged in a fluid at rest has an upward buoyancy force (upthrust) equal to the weight of the fluid displaced by the object

  • The object sinks until the weight of the fluid displaced is equal to its own weight

    • Therefore, the object floats when the magnitude of the upthrust equals the weight of the object

  • The magnitude of upthrust can be calculated by:

F space equals space rho g V

  • Where:

    • F = force in newtons (N)

    • ρ (Greek letter rho) = density in kilograms per metre cubed (kg m-3)

    • g = gravitational field strength in newtons per kg (N kg-1)

    • V = volume in metres cubed (m3)

  • Since m = ρV, upthrust is equal to F = mg which is the weight of the fluid displaced by the object

  • Archimedes’ Principle explains how ships float:

Upthrust on a boat

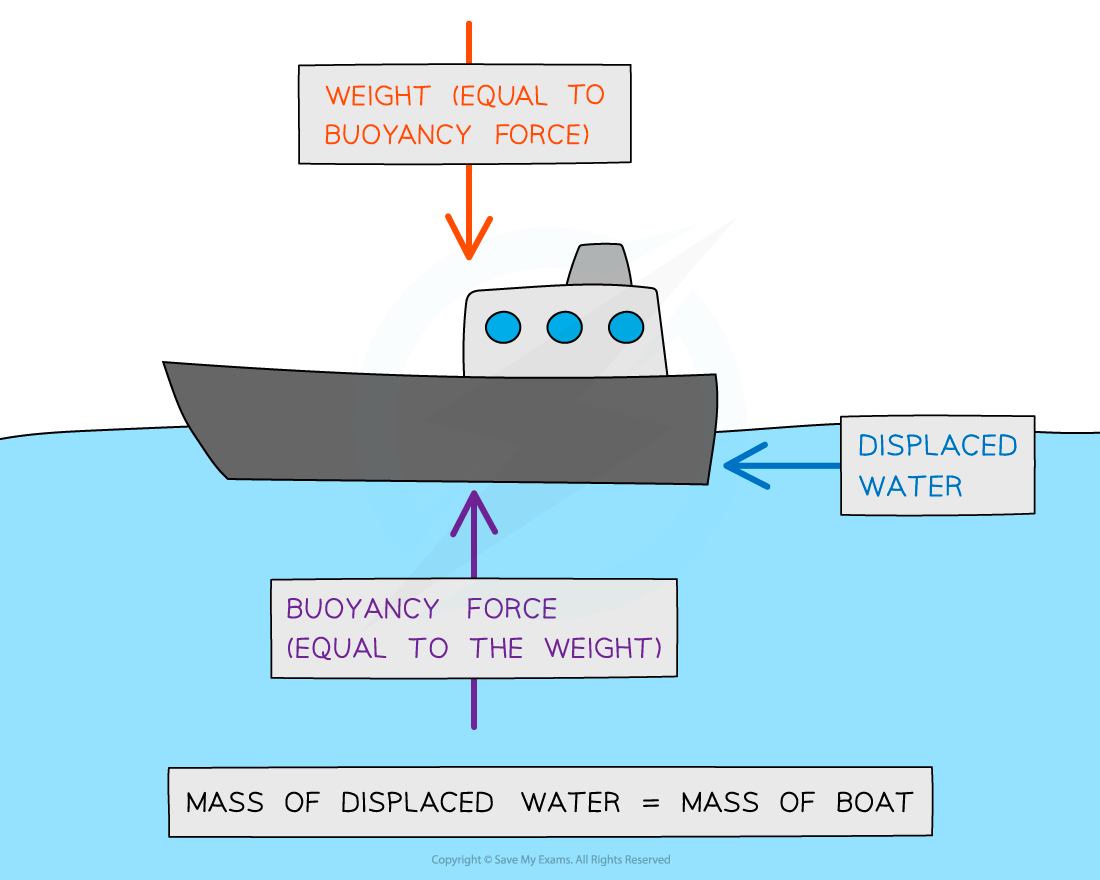
4-2-6-upthrust-on-a-boat-new

Boats float because they displace an amount of water that is equal to their weight

Worked Example

Icebergs typically float with a large volume of ice beneath the water. Ice has a density of 917 kg m-3 and a volume of Vi.

The density of seawater is 1020 kg m-3.

What fraction of the iceberg is above the water?

A. 0.10 Vi          

B. 0.90 Vi          

C. 0.97 Vi          

D. 0.20 Vi

Answer:

Step 1: List the known quantities

  • Density of ice, ρi = of 917 kg m-3

  • Volume of ice = Vi

  • Density of seawater, ρw = 1020 kg m-3

  • Volume of seawater = Vw

Step 2: Consider Archimedes' Principle

  • According to Archimedes' Principle the force of upthrust is equal to the weight of the seawater displaced by the iceberg

W subscript i space equals space m subscript i g

  • Buoyancy force is the weight of the displaced water

W subscript w space equals space m subscript w g

Step 3: Equate the forces of weight and upthrust

  • Since the iceberg is floating, its weight is exactly equal to the buoyancy force

W subscript i space equals space W subscript w

m subscript i g space equals space m subscript w g

Step 4: State the density equation and rearrange for mass

rho space equals space m over V

m space equals space rho V

Step 5: Substitute ρV for mass in the mg equivalence 

rho subscript i V subscript i g space equals space rho subscript w V subscript w g

Step 6: Determine the ratio of densities

  • Cancelling g:

rho subscript i V subscript i up diagonal strike g space equals space rho subscript w V subscript w up diagonal strike g

  • Dividing by p subscript w V subscript i

rho subscript i over rho subscript w space equals space V subscript w over V subscript i

Step 7: Solve for the volume of ice submerged underwater

V subscript w space equals space fraction numerator rho subscript i V subscript i over denominator rho subscript w end fraction

V subscript w space equals space fraction numerator 917 space V subscript i over denominator 1020 end fraction space equals space 0.9 V subscript i

  • This means that 90% of the iceberg's volume is submerged underwater

  • The correct answer is A

Examiner Tips and Tricks

Don't get confused by the two step process to find upthrust.

  • Step 1: You need the volume of the submerged object, but only because you want to know how much fluid was displaced

  • Step 2: What you really want to know is the weight of the displaced fluid.

A couple of familiar equations will help;

  • m = ρV to get mass 

   then

  • W = mg to get weight

If you are feeling particularly mathematical, you can combine your equations, so that W = ρVg

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:UpthrustNext:Work & Energy
    Author
    Reviewer
    Leander Oates

    Author: Leander Oates

    Expertise: Physics

    Leander graduated with First-class honours in Science and Education from Sheffield Hallam University. She won the prestigious Lord Robert Winston Solomon Lipson Prize in recognition of her dedication to science and teaching excellence. After teaching and tutoring both science and maths students, Leander now brings this passion for helping young people reach their potential to her work at SME.

    Caroline Carroll

    Author: Caroline Carroll

    Expertise: Physics Subject Lead

    Caroline graduated from the University of Nottingham with a degree in Chemistry and Molecular Physics. She spent several years working as an Industrial Chemist in the automotive industry before retraining to teach. Caroline has over 12 years of experience teaching GCSE and A-level chemistry and physics. She is passionate about creating high-quality resources to help students achieve their full potential.