Revision NotesExam QuestionsPast Papers
ASPhysicsCambridge (CIE)Revision Notes3. DynamicsMomentum & Newton’s Laws of MotionLinear Momentum

Linear Momentum (Cambridge (CIE) AS Physics)

Revision Note

Leander Oates

Written by: Leander Oates

Reviewed by: Caroline Carroll

Updated on

Linear momentum

  • Linear momentum, p, is defined as the product of mass and velocity

p space equals space m v

  • Where:

    • p = linear momentum in kilogram metres per second (kg m s-1)

    • m = mass in kilograms (kg)

    • v = velocity in metres per second (m s-1)

  • Momentum is a vector quantity; it has both magnitude and direction

  • It can have a positive or negative value which describes its direction in a one dimensional plane

    • If an object travelling to the right has positive momentum, an object travelling to the left (in the opposite direction) has a negative momentum

Momentum of a ball hitting a wall

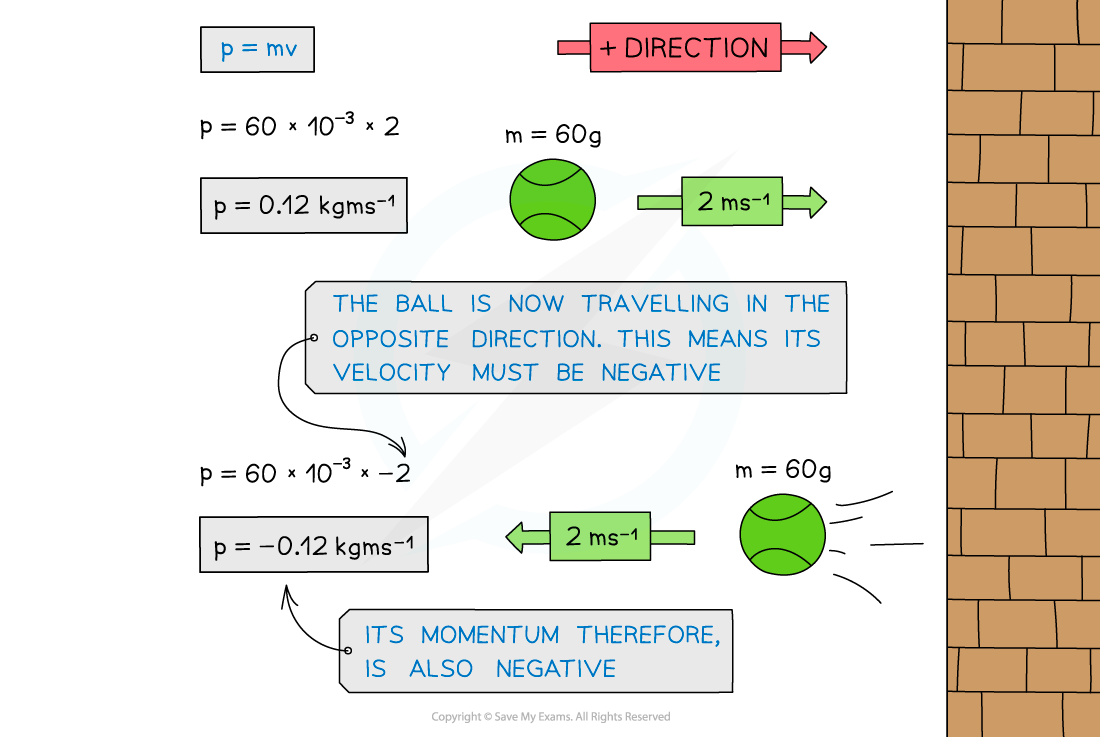
Negative momentum, downloadable AS & A Level Physics revision notes

When the ball is travelling in the opposite direction, its velocity is negative. Since momentum = mass × velocity, its momentum is also negative

Worked Example

A tennis ball of mass, m = 60 g travels at a velocity, v = 75 m s-1. A brick of mass, m = 3 kg travels at a velocity, v = 1.5 m s-1.

Determine which object has the most momentum.

3-1-3-we-momentum-comparison-question-cie-new

Answer: 

Step 1: List the known quantities and convert to SI units

  • Mass of tennis ball, m subscript T space equals space 0.06 space kg

  • Velocity of tennis ball, v subscript T space equals space 75 space straight m space straight s to the power of negative 1 end exponent

  • Mass of brick, m subscript B space equals space 3 space kg

  • Velocity of brick, v subscript B space equals space 1.5 space straight m space straight s to the power of negative 1 end exponent

Step 2: Determine the momentum of the tennis ball

p subscript T space equals space m subscript T space cross times space v subscript T

p subscript T space equals space 0.06 space cross times space 75

p subscript T space equals space 4.5 space kg space straight m space straight s to the power of negative 1 end exponent

Step 3: Determine the momentum of the brick

p subscript B space equals space m subscript B space cross times space v subscript B

p subscript B space equals space 3 space cross times space 1.5

p subscript B space equals space 4.5 space kg space straight m space straight s to the power of negative 1 end exponent

Step 4: State which object has the most momentum

  • Both objects have the same momentum

    • Even though the brick has a greater mass, it has a much lower velocity than the tennis ball

Examiner Tips and Tricks

Remember to convert the values given into SI units. It is good practice to do this before the calculation.

  • If the mass is given in grams, convert to kg by dividing the value by 1000

  • If the velocity is given in km s−1, convert to m s−1 by multiplying the value by 1000

Like with Force and Acceleration, the direction you consider positive is your choice, as long you are consistent throughout the calculation.

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Force & AccelerationNext:Force & Momentum
    Author
    Reviewer
    Leander Oates

    Author: Leander Oates

    Expertise: Physics

    Leander graduated with First-class honours in Science and Education from Sheffield Hallam University. She won the prestigious Lord Robert Winston Solomon Lipson Prize in recognition of her dedication to science and teaching excellence. After teaching and tutoring both science and maths students, Leander now brings this passion for helping young people reach their potential to her work at SME.

    Caroline Carroll

    Author: Caroline Carroll

    Expertise: Physics Subject Lead

    Caroline graduated from the University of Nottingham with a degree in Chemistry and Molecular Physics. She spent several years working as an Industrial Chemist in the automotive industry before retraining to teach. Caroline has over 12 years of experience teaching GCSE and A-level chemistry and physics. She is passionate about creating high-quality resources to help students achieve their full potential.