Revision NotesExam QuestionsPast Papers
ASPhysicsCIERevision Notes3. Dynamics3.1 Momentum & Newton’s Laws of MotionForce & Momentum

Force & Momentum (CIE AS Physics)

Revision Note

Leander

Author

Leander

Last updated

Force & momentum

  • Force is defined as the rate of change of momentum 

F space equals space fraction numerator increment p over denominator increment t end fraction

  • Where:
    • F = force in newtons (N)
    • p = momentum in kilogram metres per second (kg m s-1)
    • t = time in seconds (s)
    • Δ (the Greek letter delta) = change in

  • Change in momentum, Δp, can also be expressed as:

change in momentum = final momentum − initial momentum

increment p space equals space p subscript f i n a l end subscript space minus space p subscript i n i t a l end subscript space equals space p subscript f space minus space p subscript i 

  •  Force and momentum are vector quantities
    • They can have a positive or negative direction

 

Worked example

A car of mass 1500 kg hits a wall at an initial velocity of 15 m s-1.

It then rebounds off the wall at 5 m s-1 and comes to rest after 3.0 s.

Calculate the average force experienced by the car.

Answer:

Step 1: List the known quantities and assign direction:

  • Mass, m = 1500 kg
  • Inital velocity, vi = 15 m s-1
  • Final velocity, vf = −5 m s-1
  • Time taken, t = 3.0 s

Step 2: State the equation for force and momentum

F space equals space fraction numerator increment p over denominator increment t end fraction

Step 3: State the equation for change in momentum

increment p space equals space p subscript f space minus space p subscript i

Step 4: Calculate the initial momentum

p subscript i space equals space m space cross times space v subscript i

p subscript i space equals space 1500 space cross times space 15

p subscript i space equals space 22 space 500 space kg space straight m space straight s to the power of negative 1 end exponent

Step 5: Calculate the final momentum

p subscript f space equals space m space cross times space v subscript f

p subscript f space equals space 1500 space cross times space minus 5

p subscript f space equals space minus 7500 space kg space straight m space straight s to the power of negative 1 end exponent

Step 6: Calculate the change in momentum

increment p space equals space p subscript f space minus space p subscript i

increment p space equals space minus 7500 space minus space 22 space 500 space

increment p space equals space minus 30 space 000 space kg space straight m space straight s to the power of negative 1 end exponent

Step 7: Calculate the force

F space equals space fraction numerator increment p over denominator increment t end fraction

F space equals space fraction numerator negative 30 space 000 over denominator 3 end fraction

F space equals space minus 10 space 000 space straight N

Examiner Tip

It is easy to forget to convert values to SI units and to assign directions to values during the calculation because your brain is focused on so many other things. Unfortunately, students often lose marks for this in exams. Therefore, it is good practice to get into the habit of performing these steps before you begin the calculation. 

Direction of forces

  • The force that is equal to the rate of change of momentum is still the resultant force
  • The force on an object will be negative if the direction of the force opposes the direction of its initial velocity
  • This means that a force is exerted by the object it has collided with

 Forces acting between a car and a wall upon impact

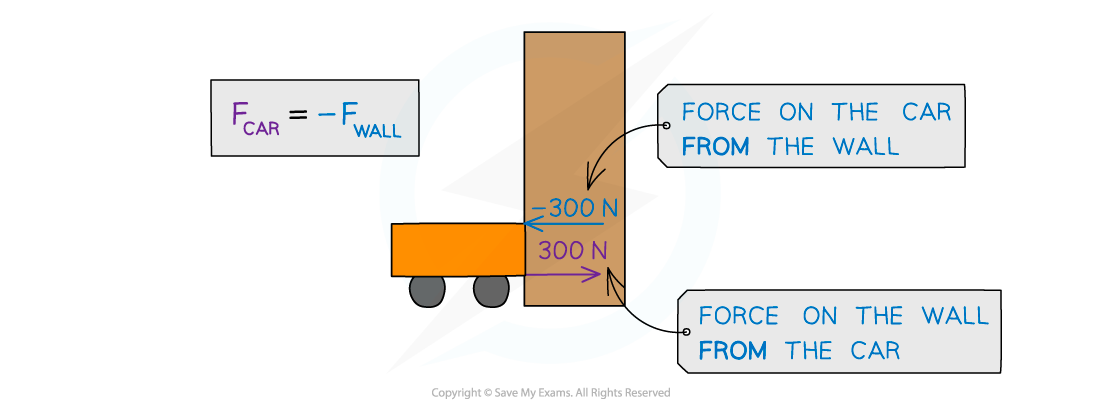
Direction of forces, downloadable AS & A Level Physics revision notes

The force exerted by the wall on car will be equal in magnitude and opposite in direction to the force exerted by the car on the wall: Fcar = –Fwall

 

  • A car collides with a wall, and the car exerts a force of 300 N on the wall
  • The wall also exerts a force of −300 N on the car
  • The force exerted by the wall on the car is equal in magnitude and opposite in direction to the force exerted by the car on the wall
  • This is Newton’s third law of motion (see Newton’s laws of motion)

Time of impact

  • The force exerted is also determined by the time taken for the impact to occur
  • The same change in momentum, over a longer period of time will exert less force, and vice versa

F space equals space fraction numerator increment p over denominator increment t end fraction

    • As Δt increases, F decreases, when Δp remains the same
    • As Δt decreases, F increases, when Δp remains the same

Worked example

A tennis ball hits a racket with a change in momentum of 0.5 kg m s-1.

The first ball has a contact time of 2.0 s. The second ball has a contact time of 0.1 s.

Determine which ball exerts the greatest force on the racket.

Answer:

Step 1: List the known quantities

  • Change in momentum, Δp = 0.5 kg m s-1
  • Change in time for the first ball, Δt1 = 2.0 s
  • Change in time for the second ball, Δt2 = 0.1 s

Step 2: Determine the force exerted by the first ball on the racket

F space equals space fraction numerator increment p over denominator increment t subscript 1 end fraction

F space equals space fraction numerator 0.5 over denominator 2.0 end fraction

F space equals space 0.25 space straight N

Step 3: Determine the force exerted by the second ball on the racket 

F space equals space fraction numerator increment p over denominator increment t subscript 2 end fraction

F space equals space fraction numerator 0.5 over denominator 0.1 end fraction

F space equals space 5.0 space straight N

Step 4: State which ball exerted the greatest force on the racket

  • The second tennis ball exerted the greatest force on the racket

Examiner Tip

In exam questions, look carefully at the cause and effect - which object is exerting a force on the other. Look out for key terms such as 'acts upon' and 'exerts'. It can be helpful to sketch a quick diagram to help you visualise the situation. This is particularly important when multiple values are given in the question, because not all of them may be relevant to the calculation.

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Linear MomentumNext:Newton's Laws of Motion
    Leander

    Author: Leander

    Expertise: Physics

    Leander graduated with First-class honours in Science and Education from Sheffield Hallam University. She won the prestigious Lord Robert Winston Solomon Lipson Prize in recognition of her dedication to science and teaching excellence. After teaching and tutoring both science and maths students, Leander now brings this passion for helping young people reach their potential to her work at SME.