Revision NotesExam QuestionsPast Papers
ASPhysicsCambridge (CIE)Revision Notes2. KinematicsEquations of MotionGradient of a Velocity-Time Graph

Gradient of a Velocity-Time Graph (Cambridge (CIE) AS Physics)

Revision Note

Ashika

Written by: Ashika

Reviewed by: Caroline Carroll

Updated on

Gradient of a velocity-time graph

  • Acceleration is any change in the velocity of an object in a given time

a c c e l e r a t i o n space equals fraction numerator space c h a n g e space i n space v e l o c i t y over denominator t i m e end fraction space equals space fraction numerator open parentheses v space minus space u close parentheses space over denominator t end fraction space equals space fraction numerator increment v space over denominator increment t end fraction

  • Where:

    • v = final velocity (m s–1) 

    • u = initial velocity (m s–1) 

    • Δv = change in velocity (m s–1) 

    • Δt = change in time (s)

  • As velocity is a vector quantity, this means that if the speed of an object changes, or its direction changes, then it is accelerating

    • An object that slows down tends to be described as ‘decelerating’

  • The gradient of a velocity-time graph is equal to the acceleration

Acceleration on a velocity-time graph

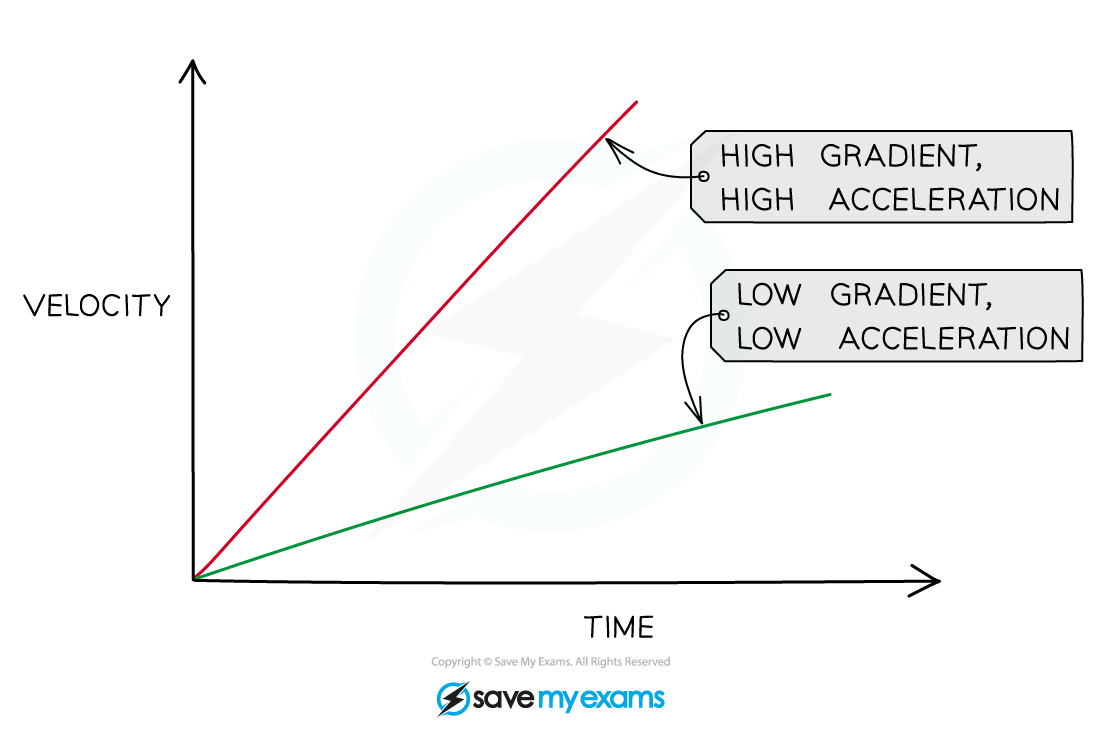
velocity-time-gradient

The larger the gradient, the larger the acceleration represented on a velocity-time graph

Worked Example

What does the velocity-time graph look like for this acceleration-time graph?

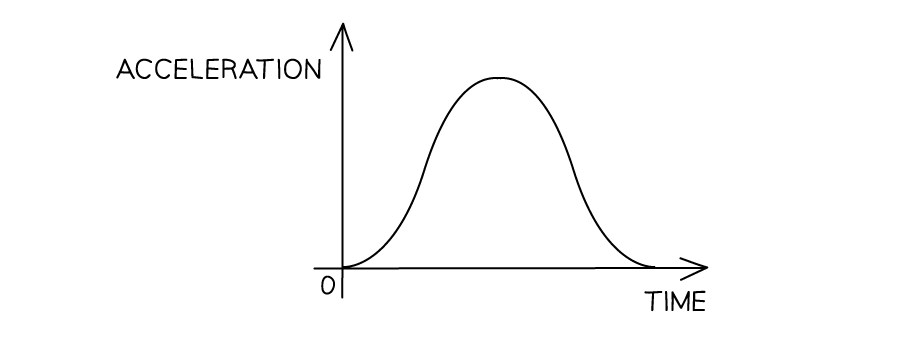
WE - V-T gradient question image, downloadable AS & A Level Physics revision notes

Answer:

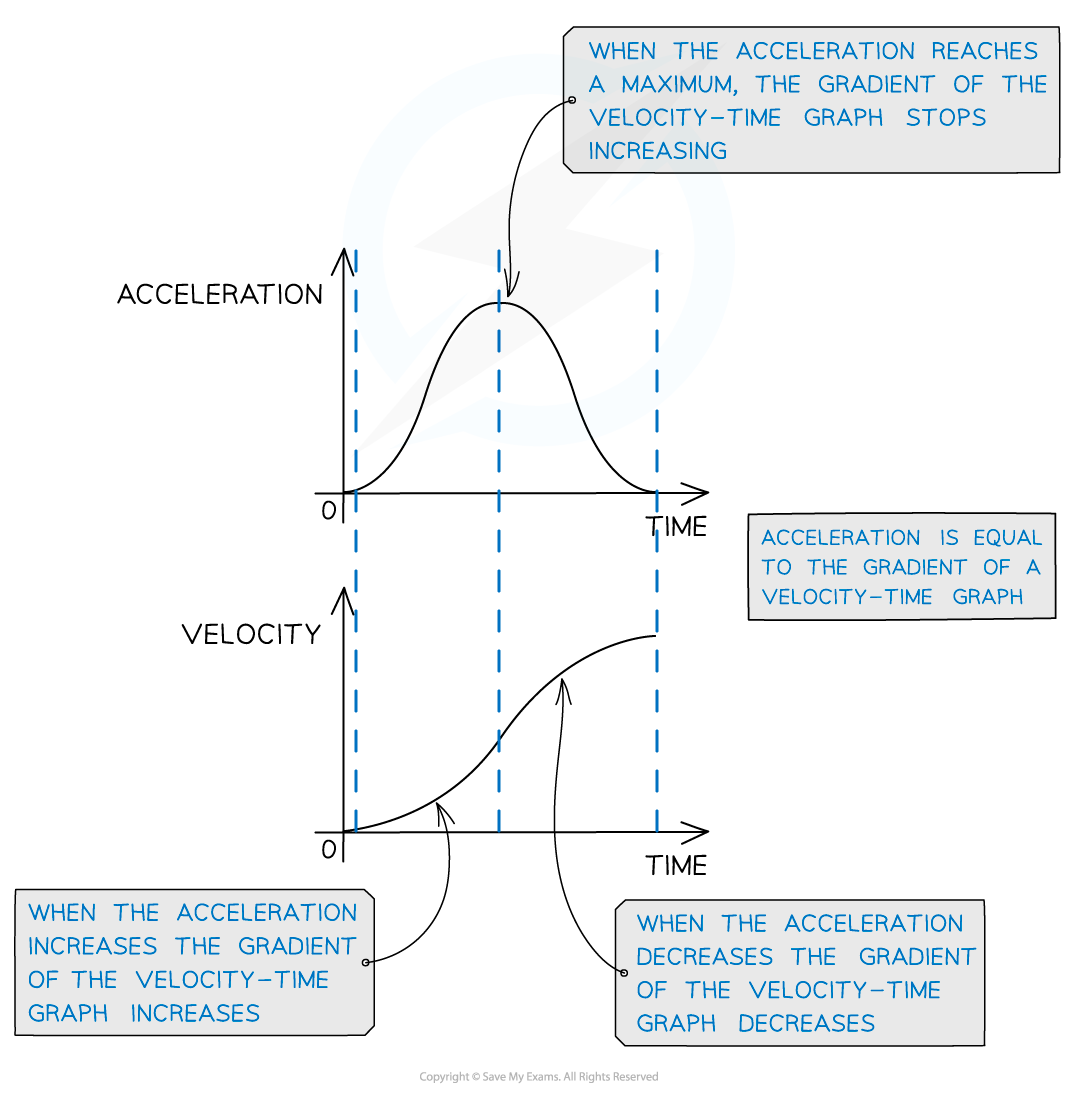
Step 1: Consider how velocity is represented on the acceleration-time graph

  • Acceleration is the gradient of a velocity-time graph

Step 2: Consider the velocity at each section of the acceleration-time graph

  • When the acceleration increases, the gradient of the velocity-time graph increases

  • When acceleration reaches a maximum, this is the maximum gradient of the velocity-time graph

  • When the acceleration decreases, the gradient of the velocity-time graph decreases

WE - V-T gradient answer image, downloadable AS & A Level Physics revision notes

Examiner Tips and Tricks

A summary of the areas under the graph and gradients for the different motion graphs are:

Gradient:

  • The gradient of a displacement-time graph is the velocity

  • The gradient of a velocity-time graph is the acceleration

Area under the graph:

  • The area under a velocity-time graph is the displacement

  • The area under an acceleration-time graph is the velocity

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Gradient of a Displacement-Time GraphNext:Deriving Kinematic Equations
    Author
    Reviewer
    Ashika

    Author: Ashika

    Expertise: Physics Project Lead

    Ashika graduated with a first-class Physics degree from Manchester University and, having worked as a software engineer, focused on Physics education, creating engaging content to help students across all levels. Now an experienced GCSE and A Level Physics and Maths tutor, Ashika helps to grow and improve our Physics resources.

    Caroline Carroll

    Author: Caroline Carroll

    Expertise: Physics Subject Lead

    Caroline graduated from the University of Nottingham with a degree in Chemistry and Molecular Physics. She spent several years working as an Industrial Chemist in the automotive industry before retraining to teach. Caroline has over 12 years of experience teaching GCSE and A-level chemistry and physics. She is passionate about creating high-quality resources to help students achieve their full potential.