Displacement, Velocity & Acceleration (Cambridge (CIE) AS Physics) : Revision Note
Defining displacement, velocity & acceleration
Distance and displacement
Distance
Distance is a measure of how far an object travels
It is a scalar quantity with magnitude only
Total running distance
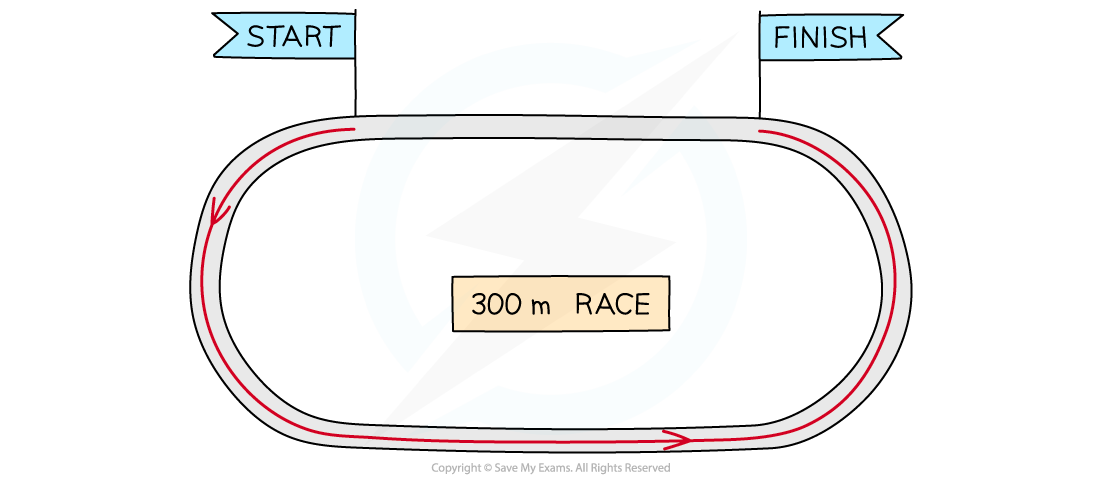
The athletes run a total distance of 300 m
Consider some athletes running a 300 m race on a 400 m track
The distance travelled by the athletes is 300 m
Displacement
Displacement is a measure of how far something is from its starting position, along with its direction
In other words, it is the change in position
It is a vector quantity with both magnitude and direction
Total distance vs total displacement
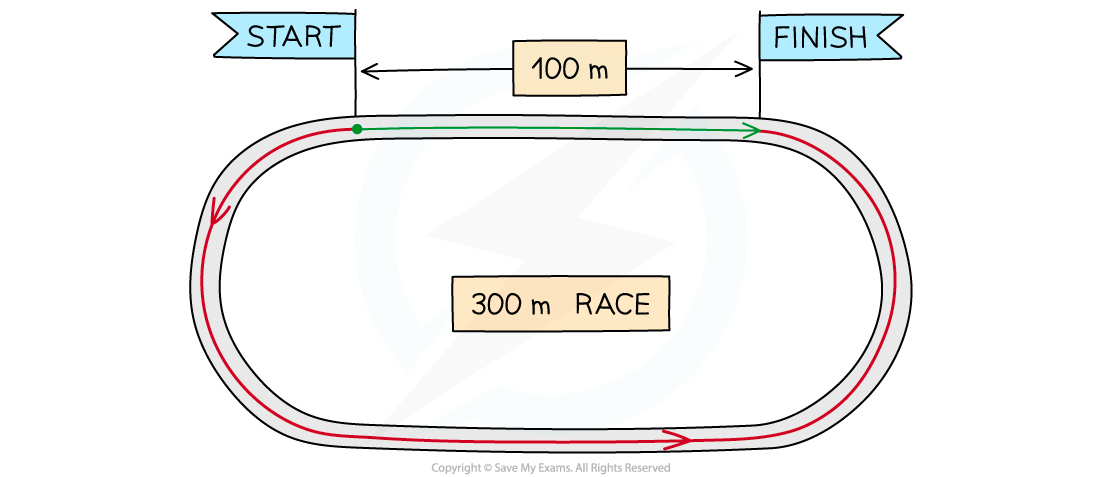
The athletes run a total distance of 300 m, but end up 100 m from where they started
Consider the same 300 m race again
The athletes have still run a total distance of 300 m (this is indicated by the arrow in red)
However, their displacement at the end of the race is 100 m to the right (this is indicated by the arrow in green)
If they had run the full 400 m, their final displacement would be zero
Distance is a scalar quantity because...
It describes how far an object has travelled overall, but not the direction it has travelled in
Displacement is a vector quantity because...
It describes how far an object is from where it started and in what direction
Speed and velocity
Speed
The speed of an object is the distance it travels every second
Speed is a scalar quantity with magnitude only
The average speed of an object is given by the equation:
The SI units for speed are meters per second (m s−1) but speed can often be measured in alternative units e.g. km h−1 or mph, when it is more appropriate for the situation
Velocity
The velocity of a moving object is similar to its speed and also describes the direction of the velocity
Velocity is defined as:
The rate of change of displacement
Velocity is, therefore, a vector quantity because it describes both magnitude and direction
Velocity is the speed in a given direction
The average velocity
of an object can be calculated using
Where:
= total displacement, or change in position, measured in (m)
= total time taken, measured in (s)
If the initial velocity u and final velocity v are known, the average velocity can also be calculated using:
Examiner Tips and Tricks
Velocity is speed in a given direction, but average velocity is not average speed in a given direction. This is because speed uses distance, and velocity uses displacement, and the magnitudes of these values can be very different for the same motion.
Acceleration
Acceleration is defined as:
The rate of change of velocity
Acceleration is a vector quantity and is measured in metres per second squared (m s–2)
It describes how much an object's velocity changes every second
The average acceleration of an object can be calculated using:
Where:
= average acceleration, measured in m s–2
= change in velocity, measured in m s–1
= total time taken, measured in s
The change in velocity is the difference between the initial and final velocity, as written below:
change in velocity = final velocity − initial velocity
Worked Example
A professor walks around her garden following the path ABCDA.
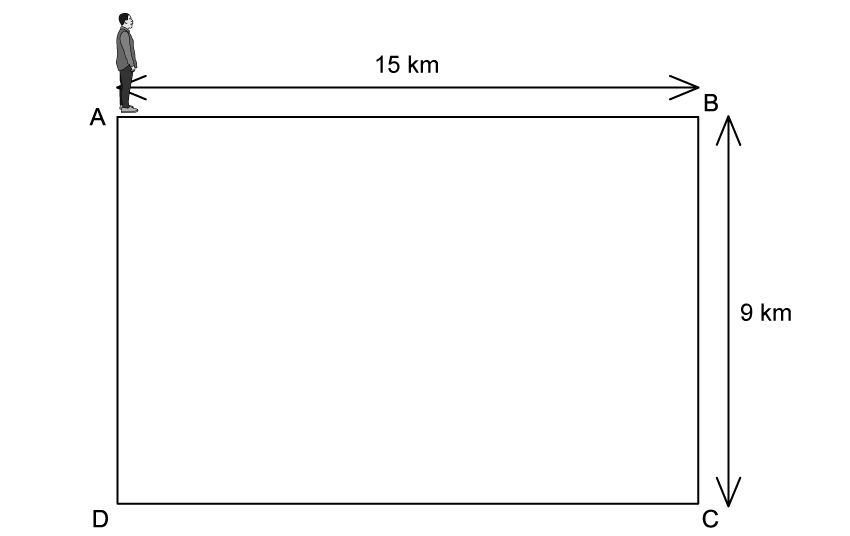
Calculate, at the end of their walk
(a) the distance the professor travels.
(b) the displacement of the professor.
Answer:
(a) The distance the professor travels is:
The total distance of each side of the rectangle
15 + 9 + 15 + 9 = 48 km
(b) The displacement of the professor is:
The displacement is how far the professor is from their original position
As they travel back to point A, the total displacement = 0 km

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?

