State what is meant by the diffraction of a wave.
State one property of a wave that changes when it is diffracted and one that remains the same.
Use words from Table 1.1 to complete the following sentence:
................................ passing through ................................ will produce a large diffraction effect.
Table 1.1

Fig. 1.1 shows a child in a hallway looking for a toy which is making a noise and emitting light.
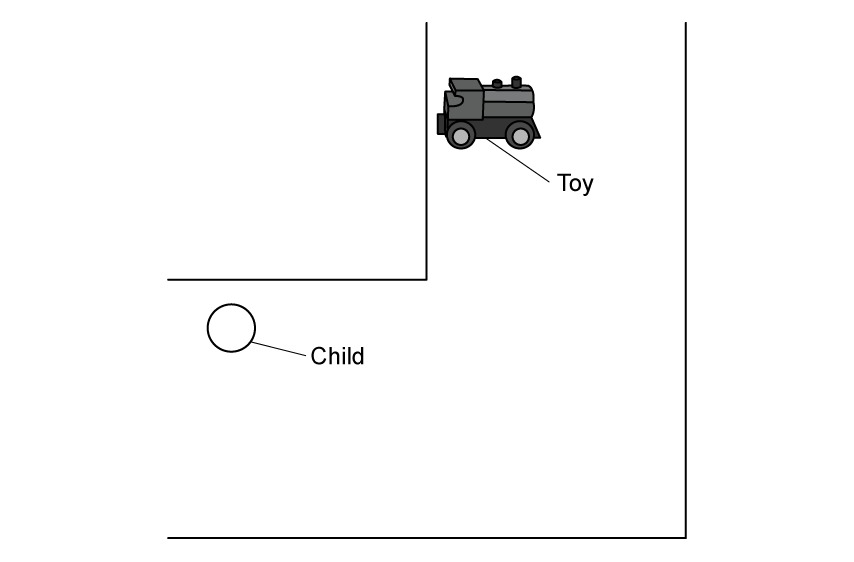
Fig. 1.1
The child can hear the sound of the toy, but cannot see the light coming from it.
Complete the following sentences by circling the correct word:
Sound waves emitted by the toy diffract / refract around the corner because the amplitude / wavelength is similar in size to the width of the hallway.
The amplitude / wavelength of light is much larger / smaller than that of the sound waves, so light is not diffracted / refracted around the corner.
Did this page help you?






