Elastic Potential Energy (CIE AS Physics)

• The work done in stretching a material is equal to the force multiplied by the distance moved
• Therefore, the area under a force-extension graph is equal to the work done to stretch the material
• The work done is also equal to the elastic potential energy stored in the material

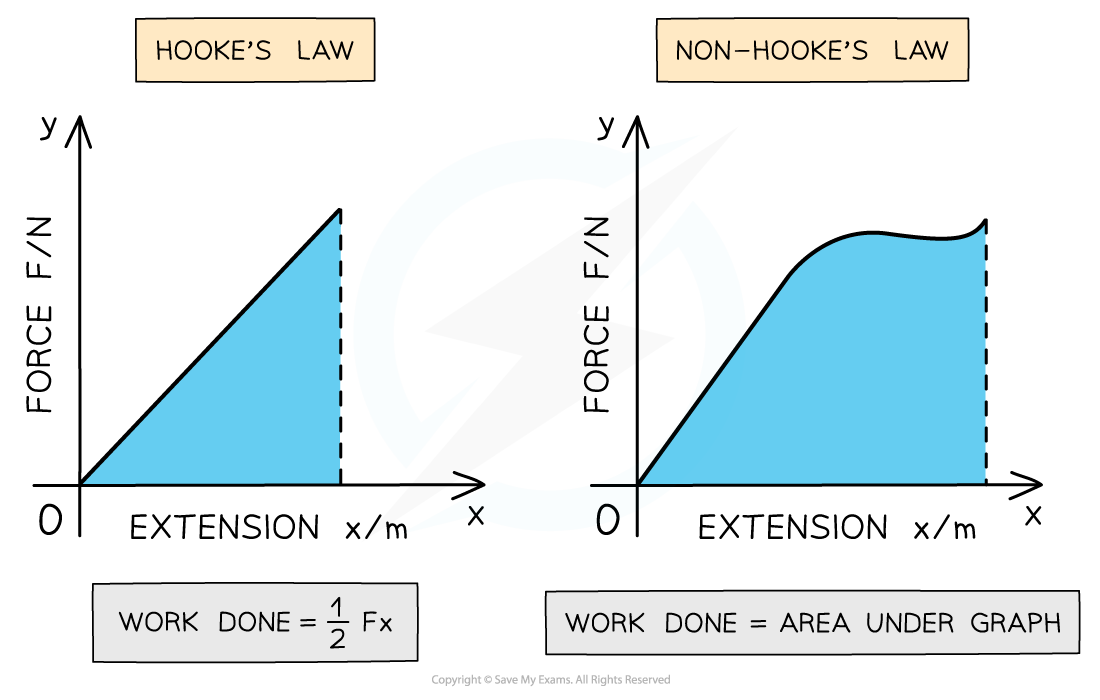
Work done is the area under the force - extension graph

• This is true for whether the material obeys Hooke’s law or not
  • For the region where the material obeys Hooke’s law, the work done is the area of a right angled triangle under the graph
  • For the region where the material doesn’t obey Hooke’s law, the area is the full region under the graph. To calculate this area, split the graph into separate segments and add up the individual areas of each

Loading and unloading

• The force-extension curve for stretching and contraction of a material that has exceeded its elastic limit, but is not plastically deformed is shown below

• The curve for contraction is always below the curve for stretching
• The area X represents the net work done or the thermal energy dissipated in the material
• The area X + Y is the minimum energy required to stretch the material to extension e

• Elastic potential energy is defined as the energy stored within a material (e.g. in a spring) when it is stretched or compressed
• It can be found from the area under the force-extension graph for a material deformed within its limit of proportionality

• A material within it’s limit of proportionality obeys Hooke’s law. Therefore, for a material obeying Hooke’s Law, elastic potential energy can be calculated using:

Elastic potential energy can be derived from Hooke’s law

• Where k is the spring constant (N m^-1) and x is the extension (m)