A student wishes to investigate what factors affect the resistance of a conducting wire.
Complete Table 1 by placing a tick ✓ in the correct column to show whether each of the quantities affects or does not affect the resistance of a conducting wire.
Table 1
Quantity | Affects Resistance | Does Not Affect Resistance |
Length |
|
|
Cross-sectional area |
|
|
Mass |
|
|
Volume |
|
|
State, in words, how resistance depends on the properties identified in part (a).
The student designs an experiment to investigate the resistivity of the conducting wire.
They measure the resistance in the wire R for varying lengths , and plot a graph, as shown in Figure 1:
Figure 1
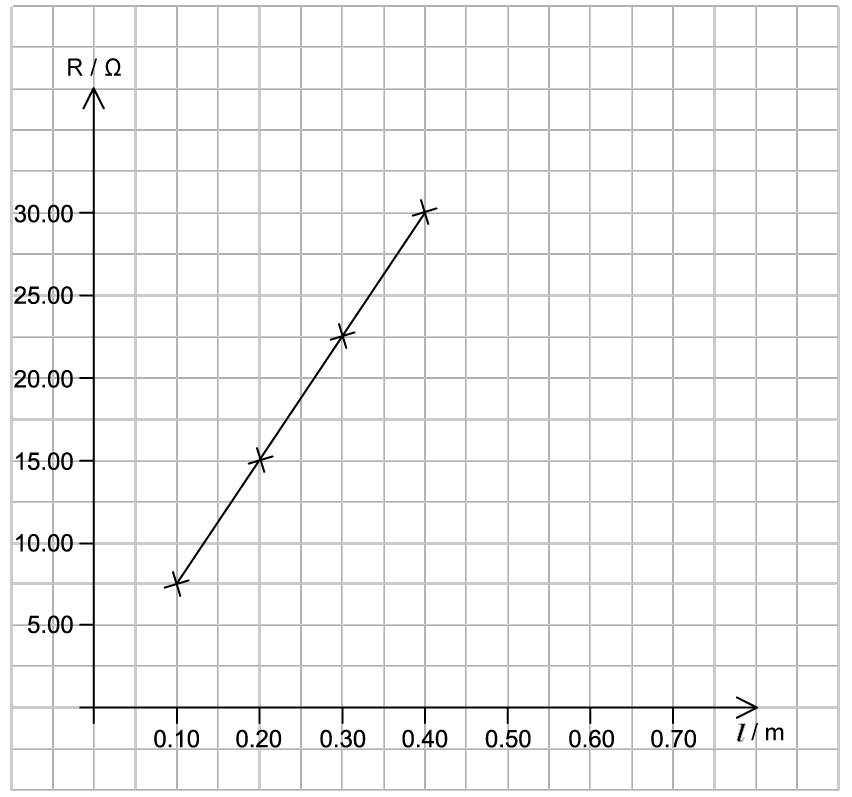
Use Figure 1 to:
(i) Calculate the gradient of the line
(ii) State an appropriate unit for the gradient
The notes in the student’s lab are shown in Figure 2:
Figure 2

The student records the cross-sectional area of the wire A = 3.8 × 10–7 m2.
(i) Suggest the measuring instrument the student likely used to measure the diameter of the wire
(ii) By referring to the gradient of the line in Figure 1, state and explain whether the student’s method to calculate the resistivity is correct
Did this page help you?















