Area Under a Force-Displacement Graph

The work done by a force acting over a distance can also be found from a force-displacement graph
If the force is not constant and is plotted against the displacement of the object:
- The work done is equal to the area under the force-displacement graph

This is because:

Work done = Force × Displacement

The work done is therefore equivalent whether there is:
- A small force over a long displacement
- A large force over a small displacement
The graph may need to be split up into sections. The total area is the sum of the areas of each section

Work Done on Graph, downloadable AS & A Level Physics revision notes

The area underneath the force-displacement graph is the work done

Worked example

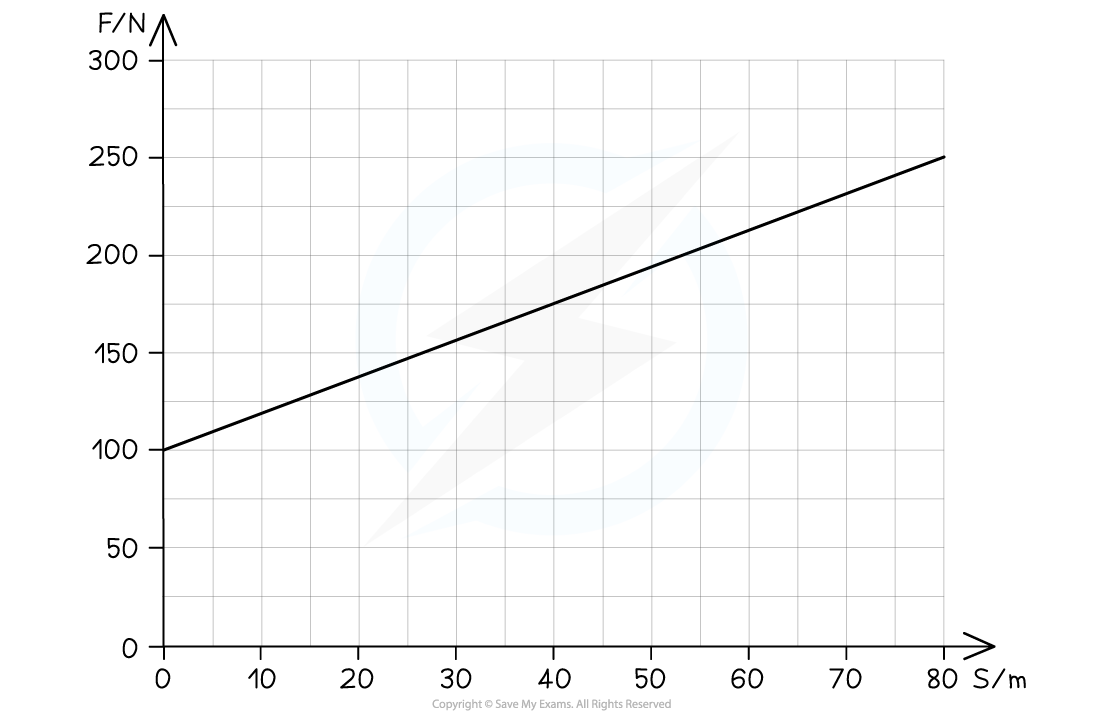
The graph shows how a force varies over a displacement of 80 m. Force Displacement Graph Worked Example, downloadable AS & A Level Physics revision notes Calculate the work done.

Step 1: Split the graph into sections

The work done is the area under the graph

The total area can be found by splitting the graph into sections A and B

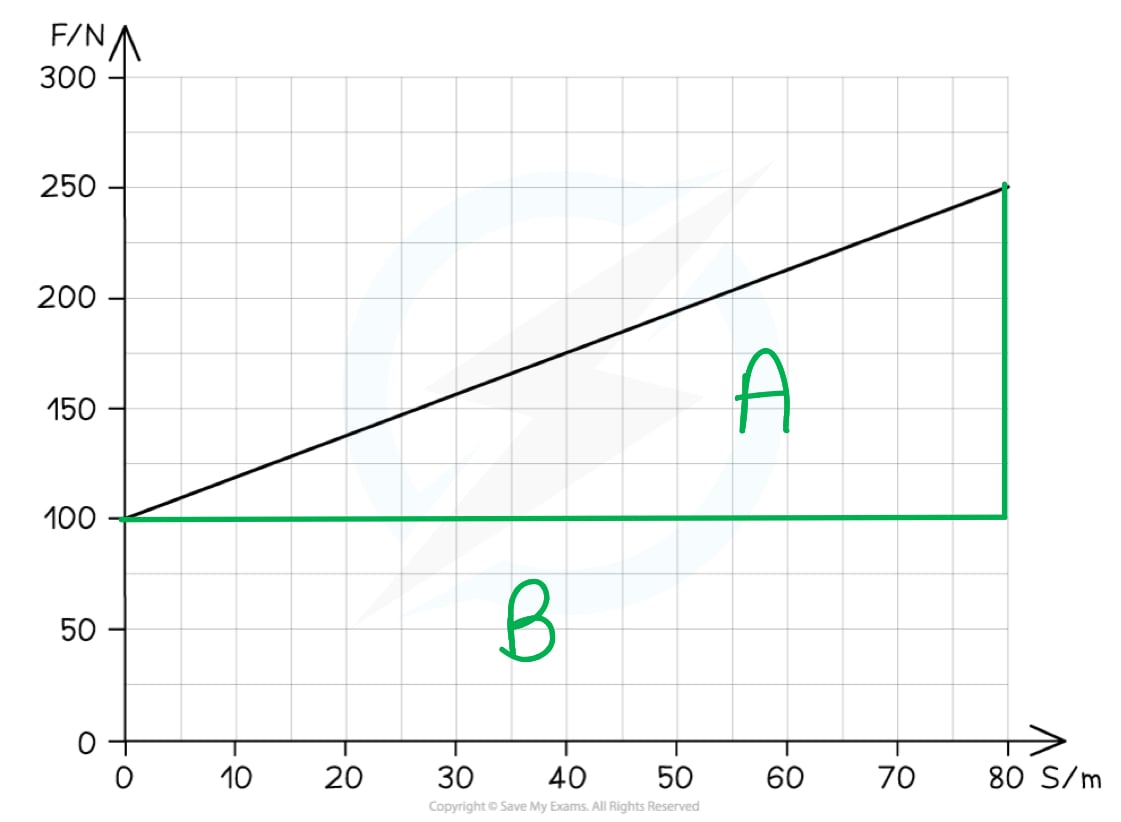
Force Displacement Graph Worked Example (2)

Step 2: Calculate the area of section A

Section A is a right-angled triangle where the area is 0.5 × base × height

0.5 × 80 × (250 – 100) = 6000 J

Step 3: Calculate the area of section B

Section B is a rectangle where the area is base × height

80 × 100 = 8000 J

Step 4: Calculate the total work done

The total work done is the sum of both areas

Work done = 6000 + 8000 = 14 000 J

Examiner Tip

Always check the units on the axes when calculating values from a graph. Sometimes the force will be given in kN or the displacement in km. These must be converted into SI units to calculate the work done in J.

Variable Forces

The force on an object may not always be constant, this is known as a variable force
This is more representative of a force in real life
If a force is constant, then the following equations can be used:

W = Fs

P = Fv

If a force is varying, the above equations cannot be used, instead, work done must be found from the area under the force-displacement graph
If a varying force increases, then an object’s acceleration increases and vice versa

Worked example

A person is pulling a suitcase through an airport with a rough surface. They apply a force of 150 N over a distance of 12 m. Afterwards, the person gets progressively tired and the applied force is linearly reduced to 60 N. The total distance through which the suitcase has moved is 25 m.

Calculate the work done by the force applied by the person over 25 m.

Step 1: Sketch a force-displacement graph and split it into sections

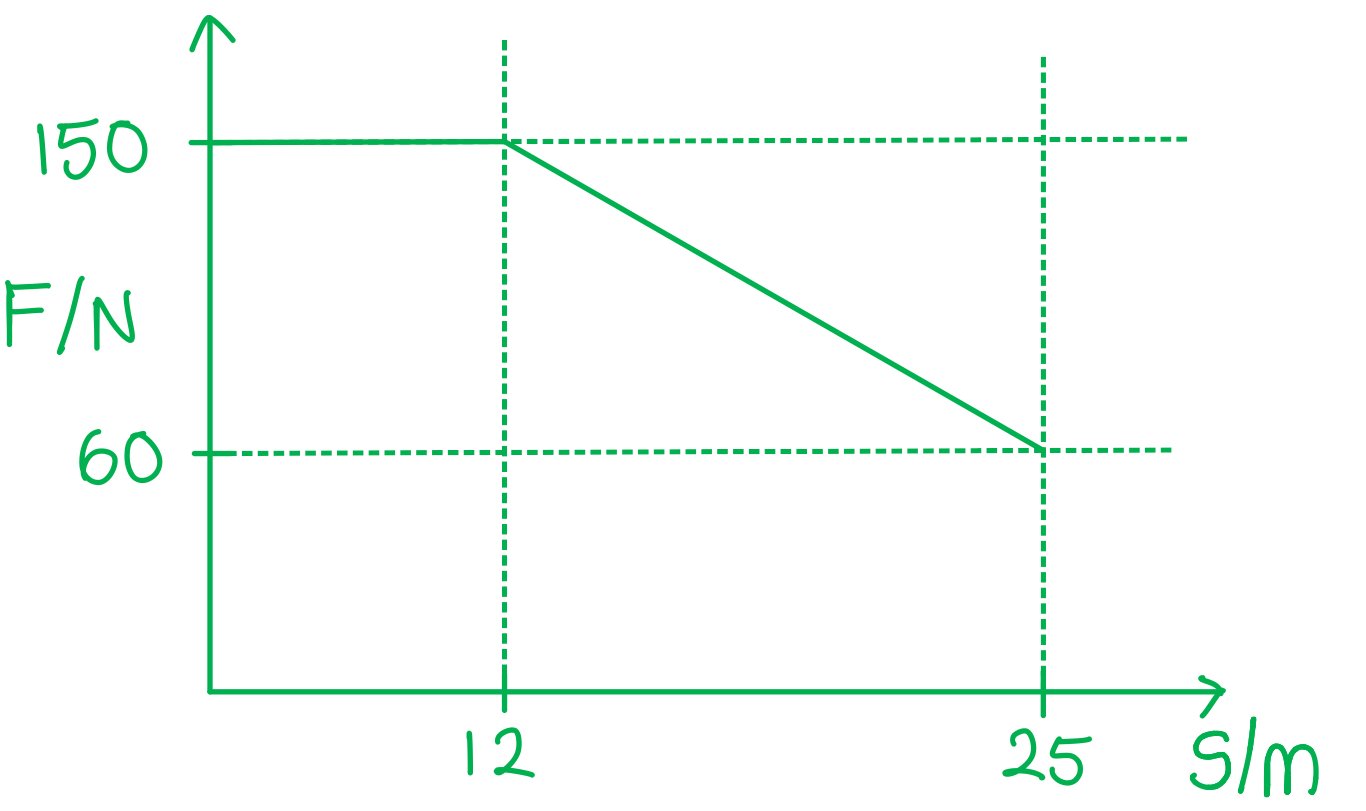
Variable Forces Worked Example 2

Step 2: Split the graph into sections

- The work done is the area under the graph
- The total area can be found by splitting the graph into sections A and B

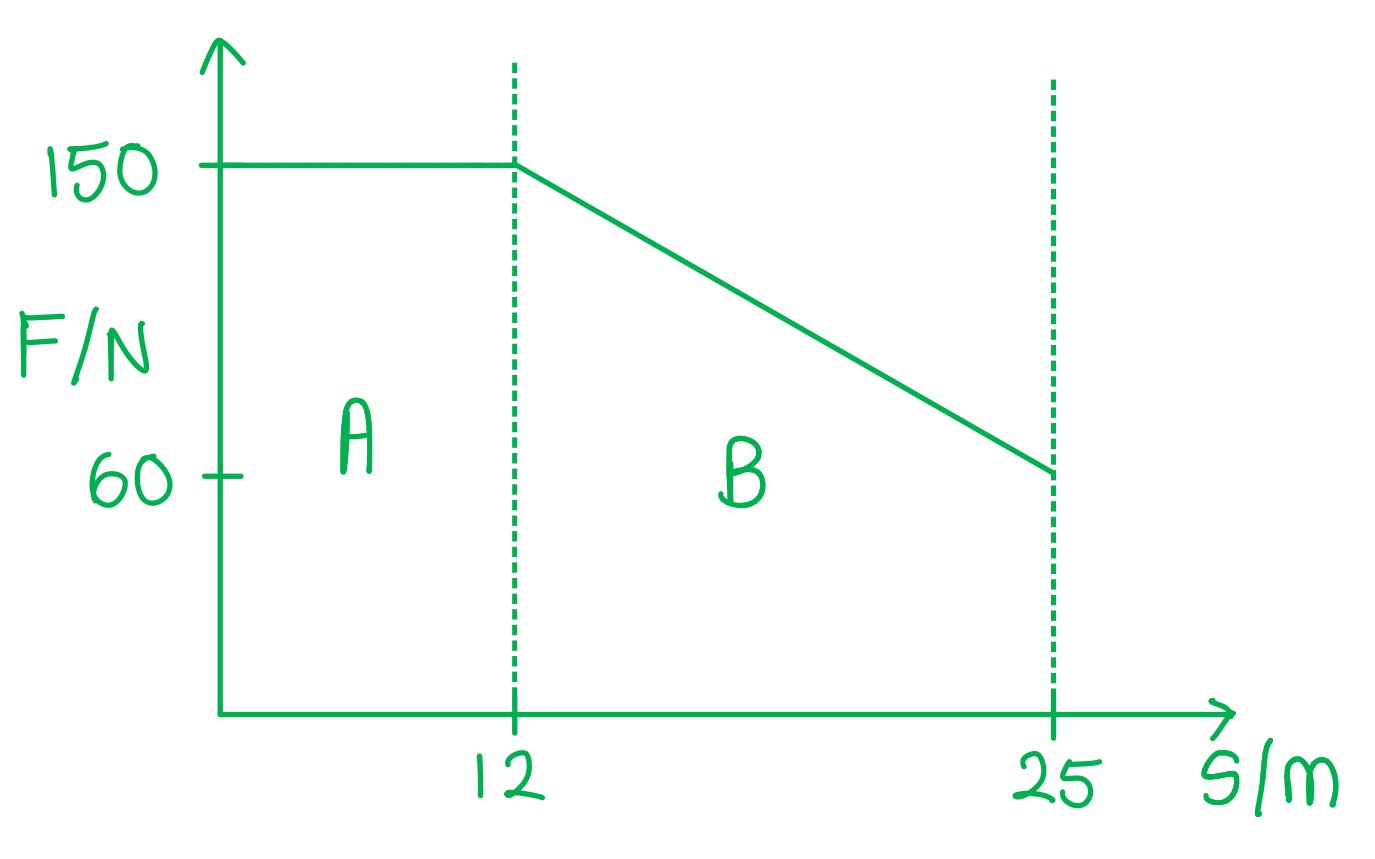
Variable Forces Worked Example

Step 3: Calculate the area of section A

- Section A is a rectangle where the area is base × height

A_A = 12 × 150 = 1800 J

Step 4: Calculate the area of section B

- Section B is a trapezium, which can be split into a right-angled triangle and a rectangle

$A_{t r i a n g l e} + A_{r e c t a n g l e} = (\frac{1}{2} \times base \times height) + (base \times height)$

$A_{B} = 0.5 (25 - 12) (150 - 60) + (25 - 12) (60 - 0)$

$A_{B} = (0.5 \times 13 \times 90) + (13 \times 60)$

$A_{B} = 585 + 780$

$A_{B} = 1365 J$

Step 5: Calculate the total work done

- The total work done is the sum of both areas

Work done = A_A + A_B = 1800 + 1365 = 3165 J

Examiner Tip

When sketching graphs, they don’t have to be to scale. However, it is important to label the key points on the x and y-axis from the question to calculate the areas underneath the graph.

Area Under a Force-Displacement Graph (AQA AS Physics)

Revision Note