Conservation of Momentum (AQA AS Physics) : Revision Note
The Principle of Conservation of Momentum
The principle of conservation of linear momentum states:
The total momentum before a collision is equal to the total momentum after a collision, provided no external force acts
Therefore:
momentum before = momentum after
Momentum is a vector quantity, therefore:
opposing vectors can cancel each other out, resulting in a net momentum of zero
an object that collides with another object and rebounds, has a positive velocity before the collision and a negative velocity after
Momentum, just like energy, is always conserved
If objects A and B collide, their momenta before and after are related by the following equation:
Where:
= initial momentum of A, measured in kg m s−1
= initial momentum of B, measured in kg m s−1
= final momentum of A, measured in kg m s−1
= final momentum of B, measured in kg m s−1
Conservation of momentum example: collision
Ball A moves with an initial velocity of
Ball A collides with Ball B which is stationary
After the collision, both balls travel in opposite directions
Taking the direction of the initial motion of Ball A as the positive direction (to the right)
The total momentum before the collision is
The total momentum after the collision is
The minus sign shows that Ball A travels in the opposite direction to the initial travel
If an object is stationary like Ball B is before the collision, then it has a momentum of 0
From the conservation of momentum, one can equate these expressions
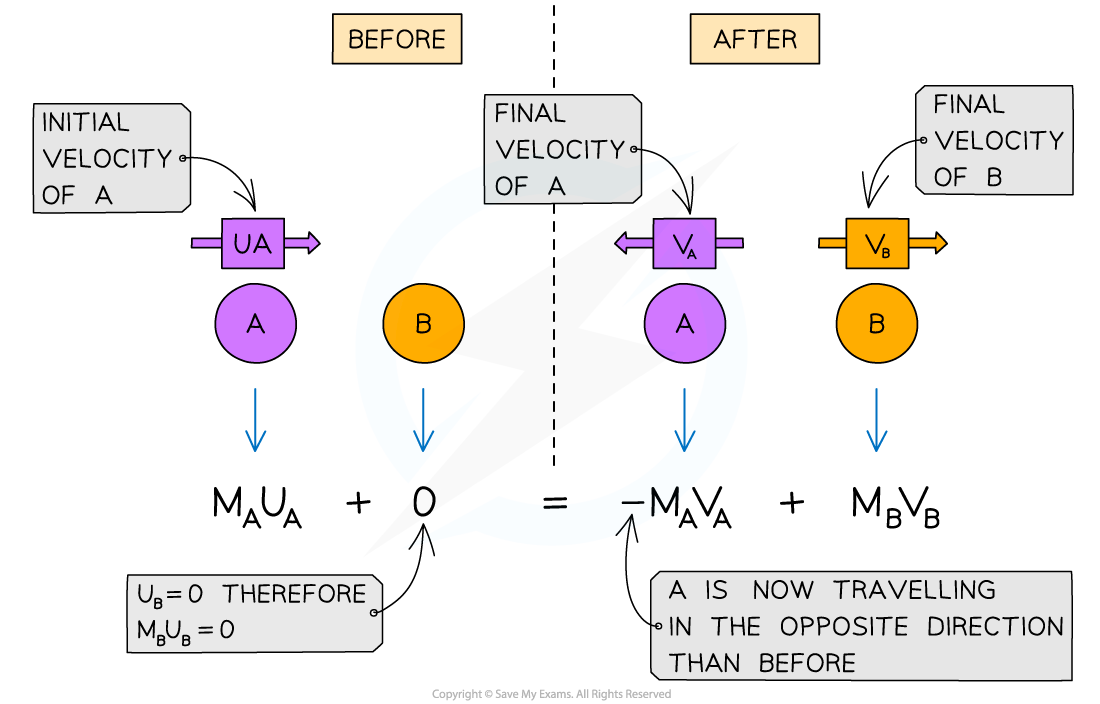
The conservation of momentum for two objects A and B colliding then moving apart
External and Internal Forces
Note that the definition of the law of conservation of momentum states that it only applies when no external forces act
External forces are forces that act on a structure or system from outside e.g. friction and weight
Internal forces are forces exchanged by the particles in the system e.g. tension in a string
Forces which are internal or external will depend on the system itself, as shown in the diagram below:

Internal and external forces on a mass on a spring
Systems with no external forces may be described as ‘closed’ or ‘isolated’
These are keywords that refer to a system that is not affected by external forces
In these systems, total momentum is conserved
For example, a swimmer diving from a boat:
The diver will move forwards, and, to conserve momentum, the boat will move backwards
This is because the momentum beforehand was zero and no external forces were present to affect the horizontal motion of the diver or the boat
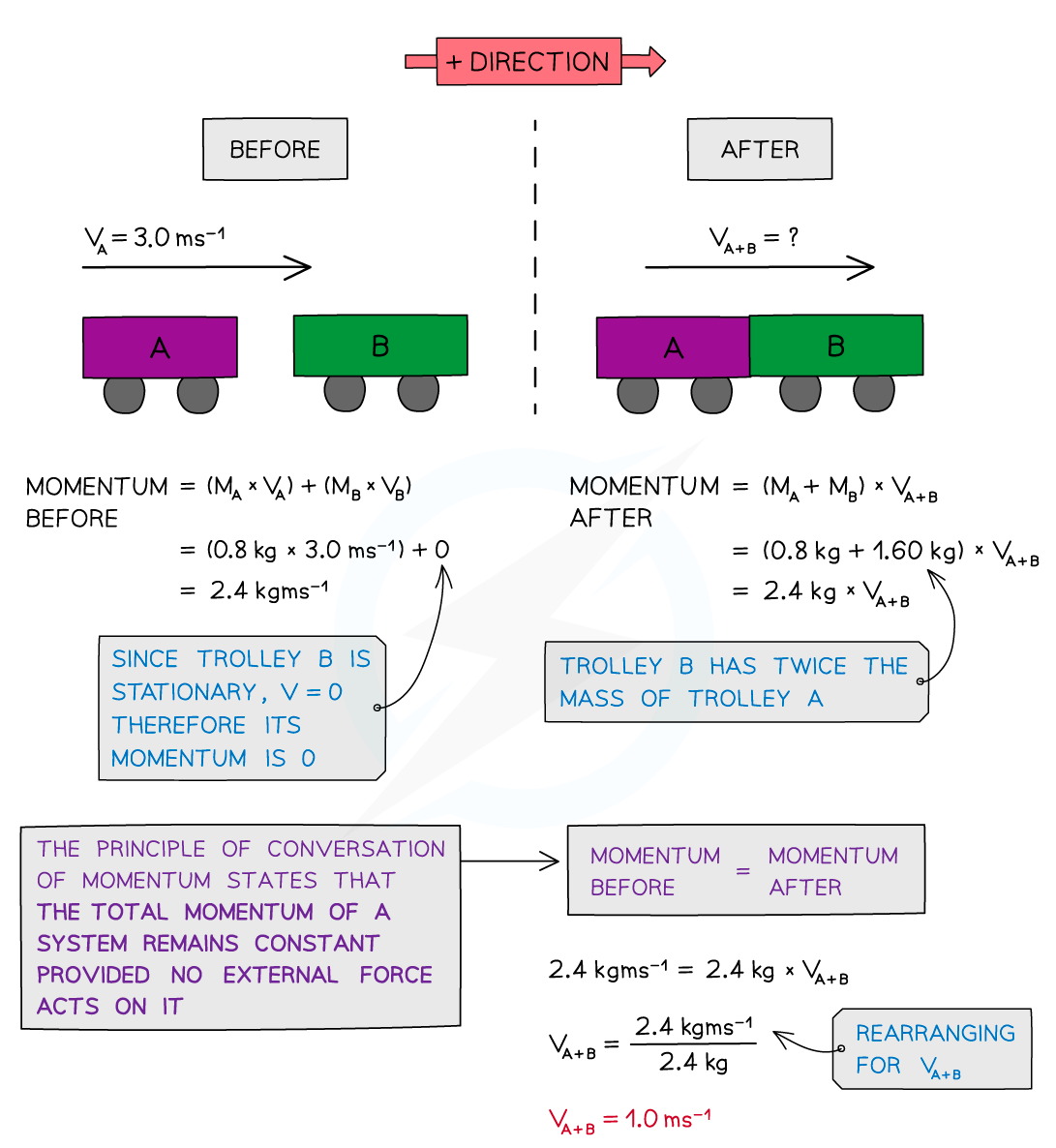
Worked Example
Trolley A of mass 0.80 kg collides head-on with stationary trolley B whilst travelling at 3.0 m s–1.
Trolley B has twice the mass of trolley A. On impact, the trolleys stick together.
Using the conservation of momentum, calculate the common velocity of both trolleys after the collision.
Answer:

You've read 1 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?

