Terminal Velocity (AQA AS Physics) : Revision Note
Terminal Velocity
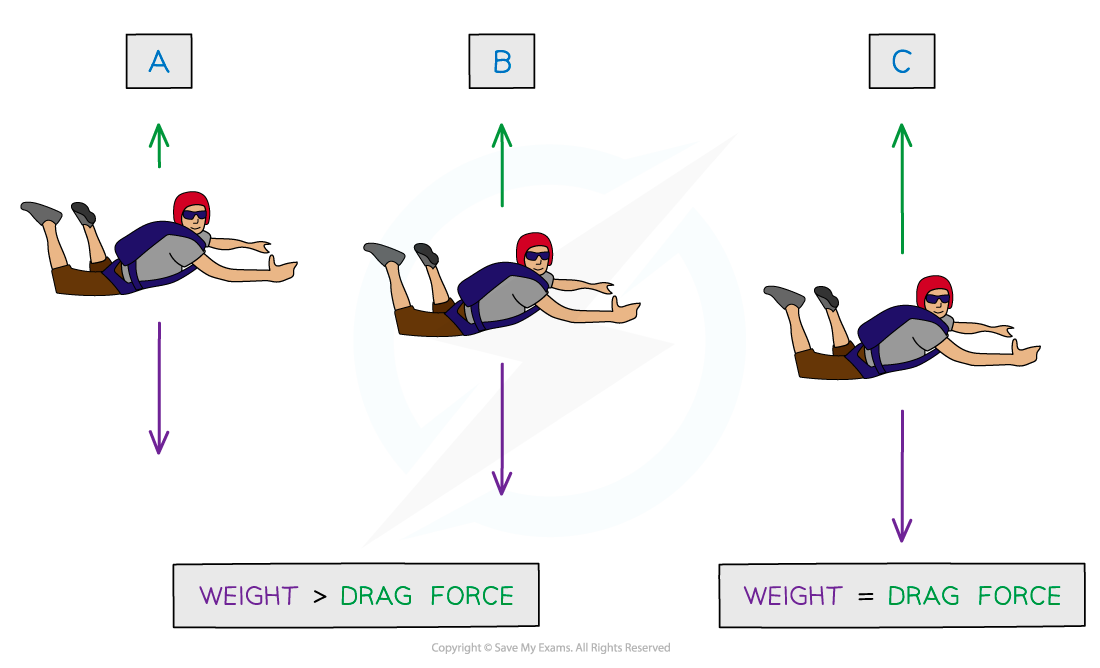
For a body in free fall, the only force acting is its weight and its acceleration g is only due to gravity.
The drag force increases as the body accelerates
This increase in velocity means the drag force also increases
Due to Newton’s Second Law, this means the resultant force and therefore acceleration decreases (recall F = ma)
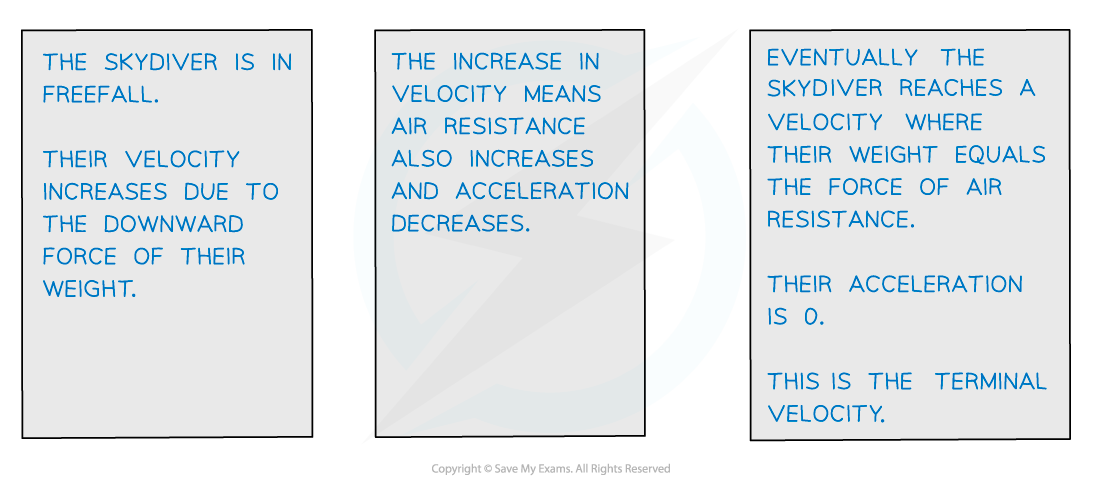
When the drag force is equal to the gravitational pull on the body, the body will no longer accelerate and will fall at a constant velocity
This the maximum velocity that the object can have and is called the terminal velocity
A skydiver in freefall reaching terminal velocity
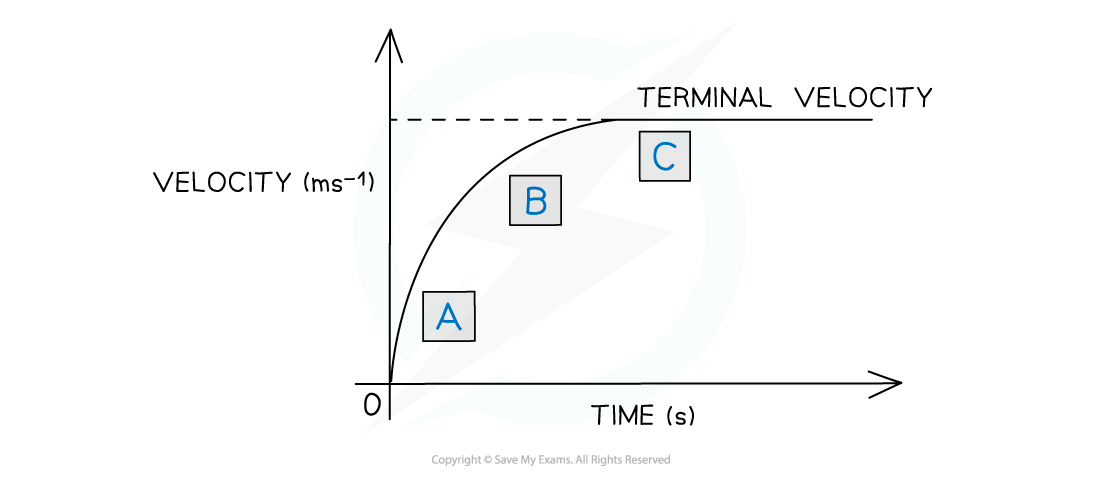
The graph shows how the velocity of the skydiver varies with time
Since the acceleration is equal to the gradient of a velocity-time graph, the acceleration decreases and eventually becomes zero when terminal velocity is reached
Worked Example
Skydivers jump out of a plane at intervals of a few seconds.
Skydivers A and B want to join up as they fall.

If A is heavier than B, who should jump first?
Answer:
Skydiver B should jump first since he will have a lower terminal velocity
This is because skydiver A has a greater mass, and hence, weight
Terminal velocity is reached when weight is equal to air resistance
Therefore, a higher terminal velocity means that skydiver A will have a greater speed, and will reach terminal velocity faster than skydiver B
Examiner Tips and Tricks
Exam questions about terminal velocity tend to involve the motion of skydivers as they fall
A common misconception is that skydivers move upwards when their parachutes are deployed - however, this is not the case, they are in fact decelerating to a lower terminal velocity
What do you think this would look like on the graph above?

You've read 1 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?


