Scalars & Vectors (AQA AS Physics)

• All quantities can be one of two types:
  • a scalar
  • a vector

Scalars

• Scalars are quantities that have magnitude but not direction
  • For example, mass is a scalar quantity because it has magnitude but no direction 

Vectors

• Vectors are quantities that have both magnitude and direction
  • For example, weight is a vector quantity because it is a force and has both magnitude and direction

Distance and displacement

• Distance is a measure of how far an object has travelled, regardless of direction
  
  • Distance is the total length of the path taken
  • Distance, therefore, has a magnitude but no direction
  • So, distance is a scalar quantity

• Displacement is a measure of how far it is between two points in space, including the direction
  
  • Displacement is the length and direction of a straight line drawn from the starting point to the finishing point
  • Displacement, therefore, has a magnitude and a direction
  • So, displacement is a vector quantity

What is the difference between distance and displacement?

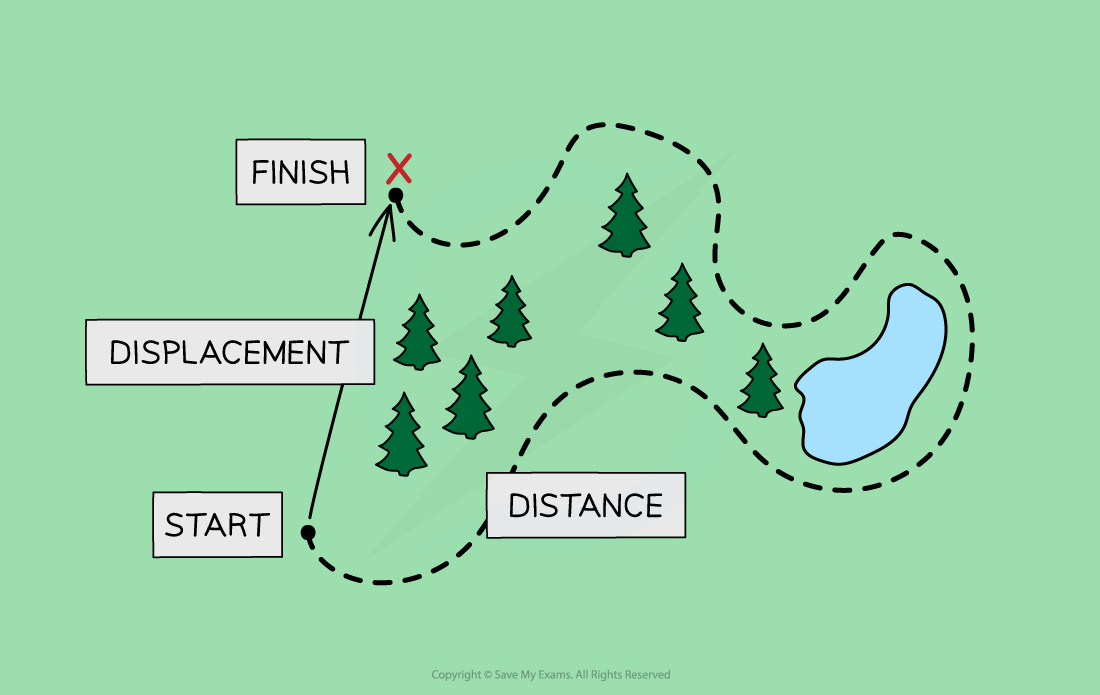
Displacement is a vector quantity while distance is a scalar quantity

• When a student travels to school, there will probably be a difference in the distance they travel and their displacement
  • The overall distance they travel includes the total lengths of all the roads, including any twists and turns
  • The overall displacement of the student would be a straight line between their home and school, regardless of any obstacles, such as buildings, lakes or motorways, along the way

Speed and velocity

• Speed is a measure of the distance travelled by an object per unit time, regardless of the direction
  • The speed of an object describes how fast it is moving, but not the direction it is travelling in
  • Speed, therefore, has magnitude but no direction
  • So, speed is a scalar quantity

• Velocity is a measure of the displacement of an object per unit time, including the direction
  • The velocity of an object describes how fast it is moving and which direction it is travelling in
  • An object can have a constant speed but a changing velocity if the object is changing direction
  • Velocity, therefore, has magnitude and direction
  • So, velocity is a vector quantity

Examples of scalars & vectors

• The table below lists some common examples of scalar and vector quantities

Table of scalars and vectors

• Vectors are represented by an arrow
  • The arrowhead indicates the direction of the vector
  • The length of the arrow represents the magnitude

• Vectors can be combined by adding them to produce the resultant vector
  • The resultant vector is sometimes known as the ‘net’ vector (eg. the net force)

• There are two methods that can be used to add vectors
  • Calculation – if the vectors are perpendicular
  • Scale drawing – if the vectors are not perpendicular

Vector Calculation

• Vector calculations will be limited to two vectors at right angles
• This means the combined vectors produce a right-angled triangle and the magnitude (length) of the resultant vector is found using Pythagoras’ theorem

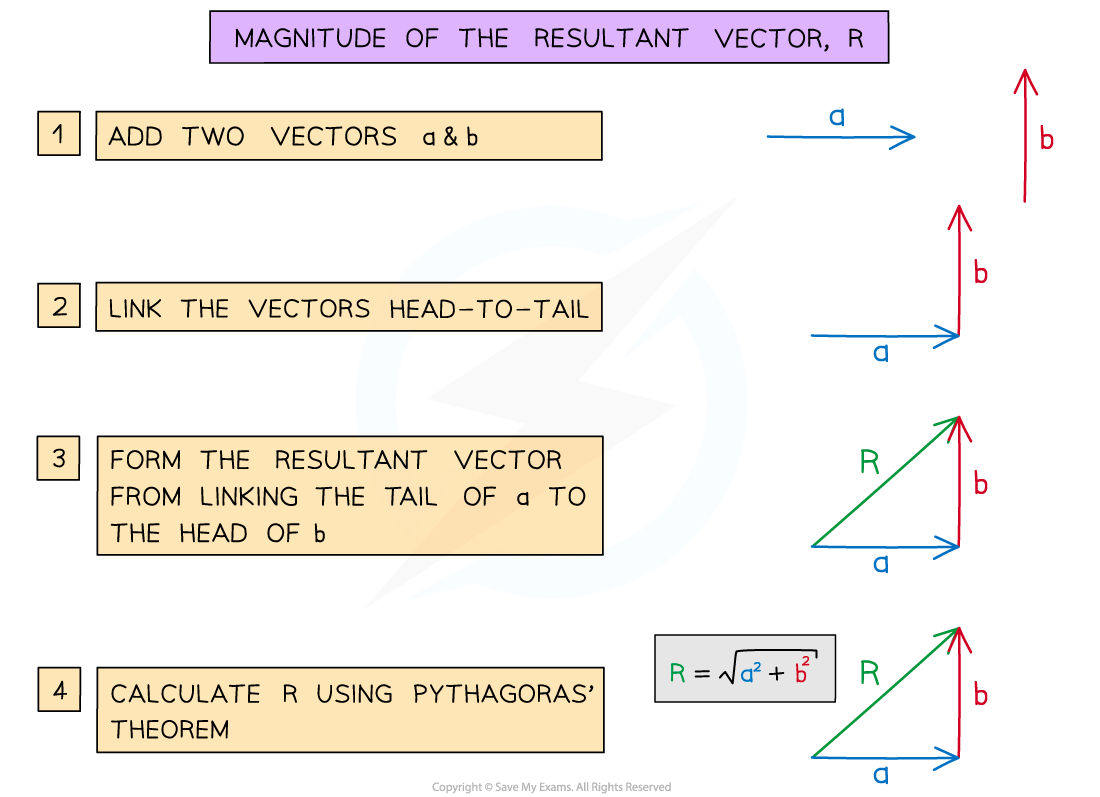
The magnitude of the resultant vector is found by using Pythagoras’ Theorem

• The direction of the resultant vector is found from the angle it makes with the horizontal or vertical
  • The question should imply which angle it is referring to (ie. Calculate the angle from the x-axis)

• Calculating the angle of this resultant vector from the horizontal or vertical can be done using trigonometry
  • Either the sine, cosine or tangent formula can be used depending on which vector magnitudes are calculated

The direction of vectors is found by using trigonometry

Scale Drawing

• When two vectors are not at right angles, the resultant vector can be calculated using a scale drawing
  • Step 1: Link the vectors head-to-tail if they aren’t already
  • Step 2: Draw the resultant vector using the triangle or parallelogram method
  • Step 3: Measure the length of the resultant vector using a ruler
  • Step 4: Measure the angle of the resultant vector (from North if it is a bearing) using a protractor

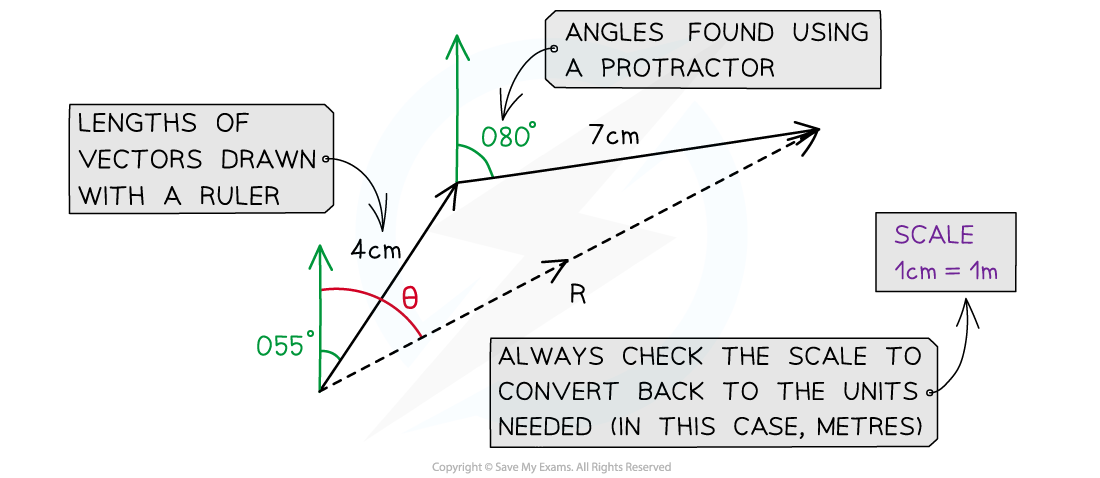
A scale drawing of two vector additions. The magnitude of resultant vector R is found using a rule and its direction is found using a protractor

• Note that with scale drawings, a scale may be given for the diagram such as 1 cm = 1 km since only limited lengths can be measured using a ruler
• The final answer is always converted back to the units needed in the diagram
  • Eg. For a scale of 1 cm = 2 km, a resultant vector with a length of 5 cm measured on your ruler is actually 10 km in the scenario

• There are two methods that can be used to combine vectors: the triangle method and the parallelogram method
• To combine vectors using the triangle method:
  • Step 1: link the vectors head-to-tail
  • Step 2: the resultant vector is formed by connecting the tail of the first vector to the head of the second vector

• To combine vectors using the parallelogram method:
  • Step 1: link the vectors tail-to-tail
  • Step 2: complete the resulting parallelogram
  • Step 3: the resultant vector is the diagonal of the parallelogram

Vector Addition

Vector Subtraction