The Diffraction Grating (AQA AS Physics) : Revision Note
The Diffraction Grating
A diffraction grating is a piece of optical equipment that also creates a diffraction pattern when it diffracts:
Monochromatic light into bright and dark fringes
White light into its different wavelength components
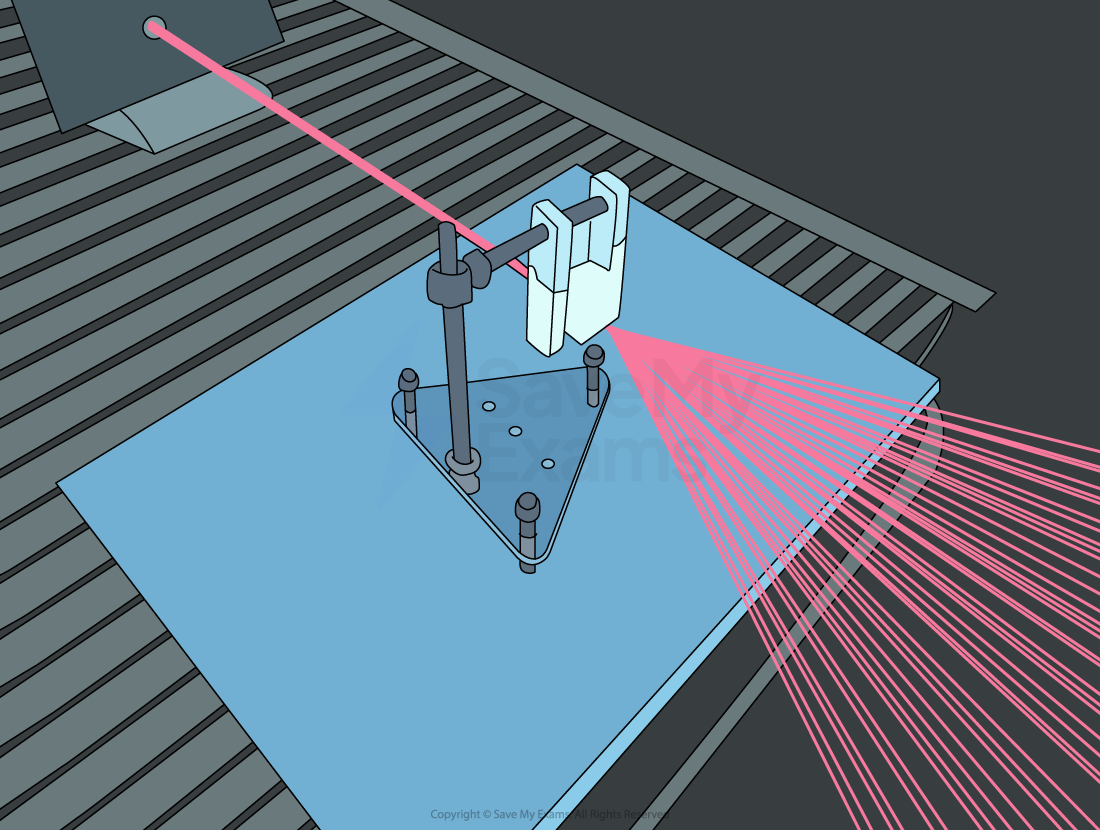
A laser light is diffracted using a diffraction grating
A diffraction grating consists of a large number of very thin, equally spaced parallel slits carved into a glass plate
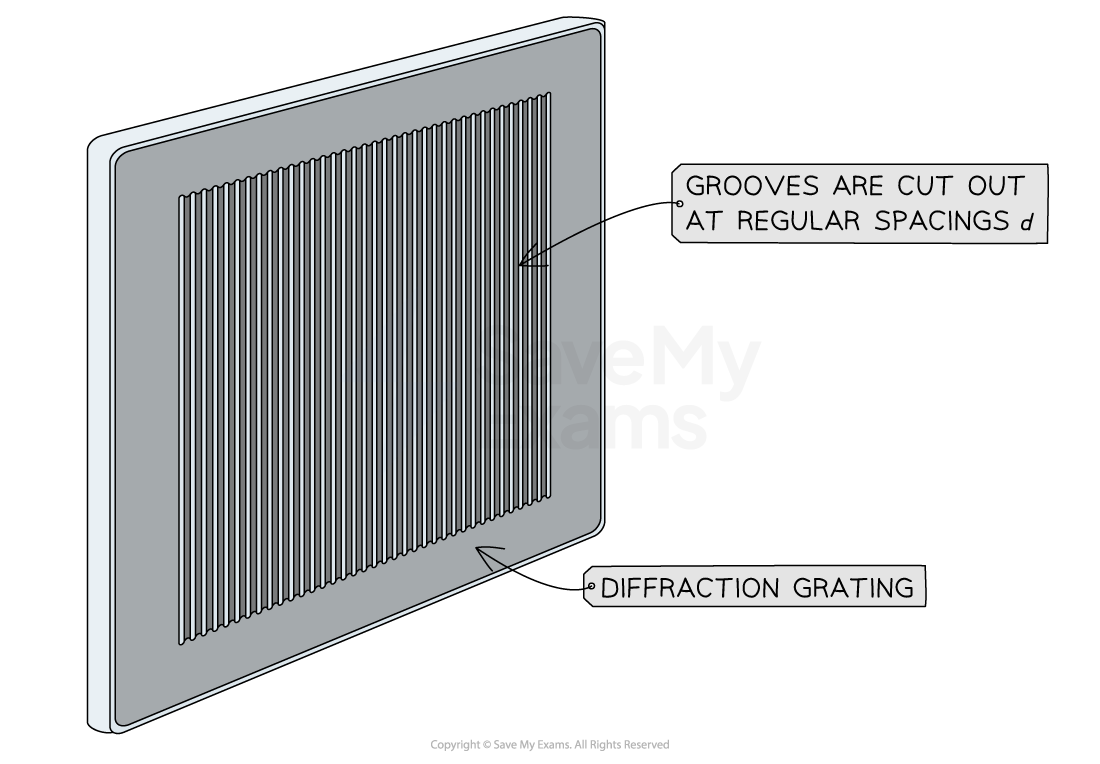
A diffraction grating consists of many parallel equally spaced slits cut into the glass plate
When you look closely at a diffraction grating you can see the curved shape of the slits
The Diffraction Grating Equation
Diffraction gratings are useful because they create a sharper pattern than a double slit
This means their bright fringes are narrower and brighter while their dark regions are wider and darker
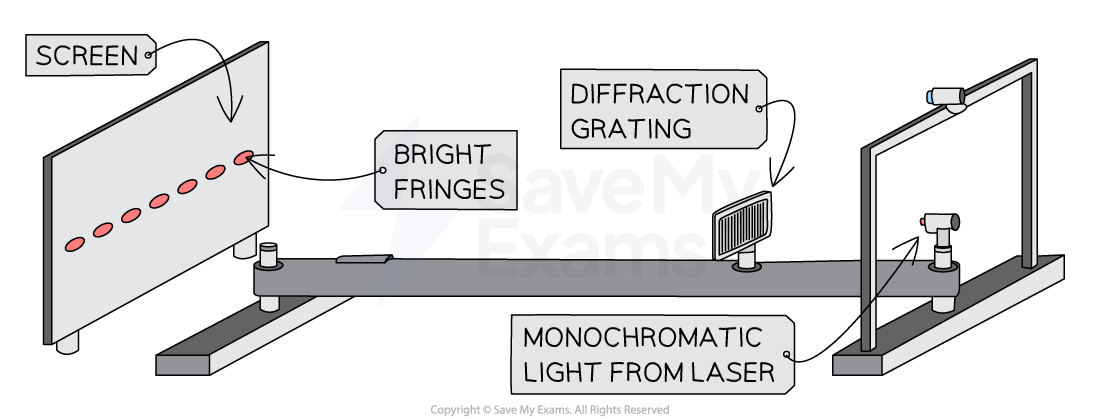
A diffraction grating is used to produce narrow bright fringes when laser light is diffracted through it
Just like for single and double-slit diffraction the regions where constructive interference occurs are also the regions of maximum intensity
Their location can be calculated using the diffraction grating equation
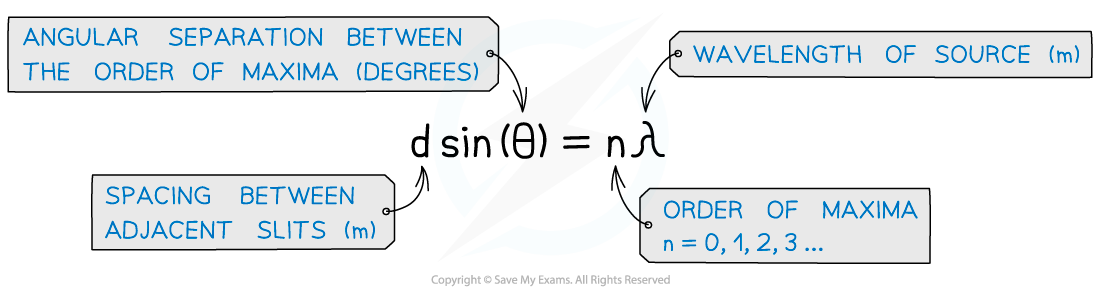
Where:
n is the order of the maxima, the number of the maxima away from the central (n = 0)
d is the distance between the slits on the grating (m)
θ is the angle of diffraction of the light of order n from the normal as it leaves the diffraction grating (°)
λ is the wavelength of the light from the source (m)
Slit Spacing
Diffraction gratings come in different sizes
The sizes are determined by the number of lines per millimetre (lines / mm) or lines per m
This is represented by the symbol N
d can be calculated from N using the equation
If N is given in terms of lines per mm then d will be in mm
If N is given in terms of lines per m then d will be in m
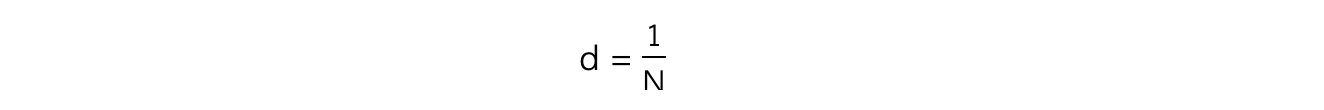
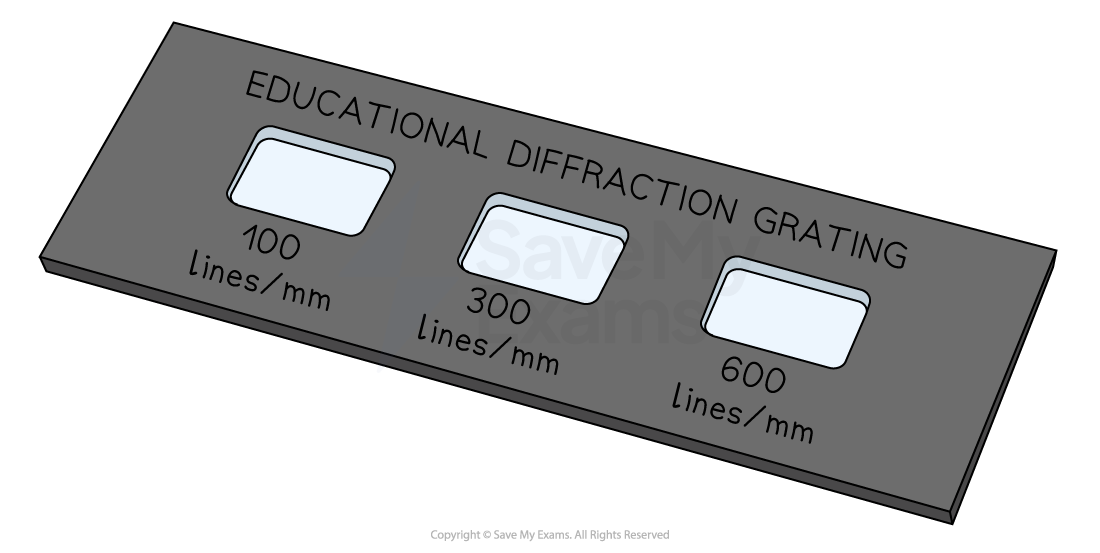
Diffraction gratings come in different sizes according to the number of lines per mm
Angular Separation
The angular separation of each maxima is calculated by rearranging the grating equation to make θ the subject
The angle θ is taken from the centre meaning the higher orders of n are at greater angles
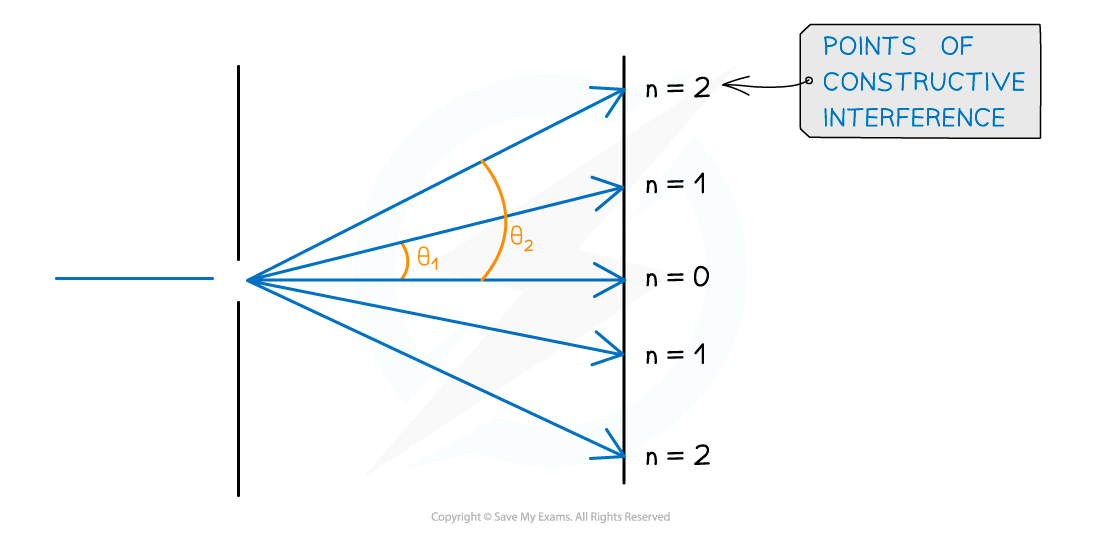
Angular separation increases as the order of maxima increases
The angular separation between two angles is found by subtracting the smaller angle from the larger one
The angular separation between the first and second maxima at n1 and n2 is θ2 – θ1
Orders of Maxima
The maximum angle of diffraction with which maxima can be seen is when the beam is at right angles to the diffraction grating
This means θ = 90o and sin θ = 1
The highest order of maxima visible is therefore calculated by the equation:
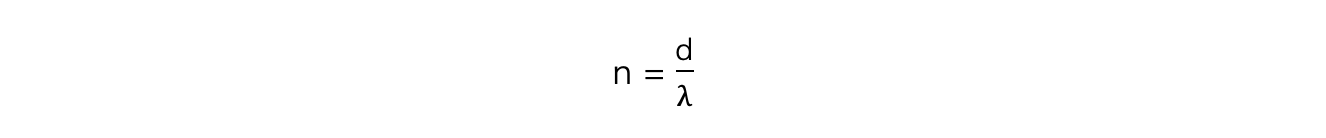
Since n is an integer number of maxima, if the value obtained is a decimal it must be rounded down to determine the highest-order visible
E.g If n is calculated as 2.7 then n = 2 is the highest-order visible
Worked Example
An experiment was set up to investigate light passing through a diffraction grating with a slit spacing of 1.7 µm. The fringe pattern was observed on a screen. The wavelength of the light is 550 nm.
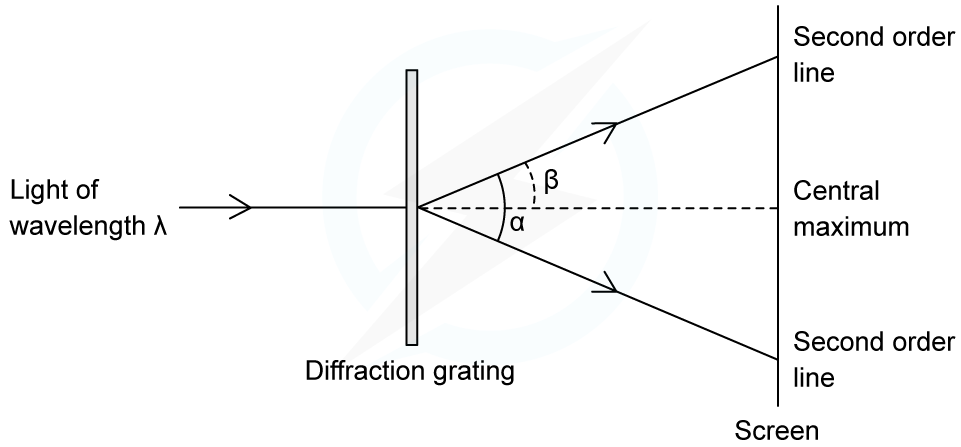
Calculate the angle α between the two second-order lines.
Answer:

Examiner Tips and Tricks
Take care that the angle θ is the correct angle taken from the centre and not the angle taken between two orders of maxima.
Derivation of the Diffraction Grating Equation
When light passes through the slits of the diffraction grating, the path difference at the zeroth order maximum is zero
At the first order maxima, there is constructive interference, hence the path difference is λ
Therefore, at the nth order maxima, the path difference is equal to nλ

Using this diagram and trigonometry, the diffraction grating equation can be derived
Using trigonometry, an expression for the first order maxima can be written:

Where:
θ = the angle between the normal and the maxima
λ = the wavelength of the light (m)
d = the slit separation (m)
This means, for n = 1:

Similarly, for n = 2, where the path difference is 2λ:

Therefore, in general, where the path difference is nλ:

A small rearrangement leads to the equation for the diffraction grating:
d sin θn = nλ
Applications of Diffraction Gratings
Diffraction gratings are useful for separating light of different wavelengths with high-resolution
They are used in spectrometers to:
Analyse light from stars
Analyse the composition of a star
Chemical analysis
Measure red shift / rotation of stars
Measure the wavelength / frequency of light from a star
Observe the spectra of materials
Analyse the absorption / emission spectra in stars
Diffraction gratings also play a role in X-ray crystallography:
X-rays are directed at a thin crystal sheet which acts as a diffraction grating to form a diffraction pattern
This is because the wavelength of X-rays is similar in size to the gaps between the atoms
This diffraction pattern can be used to measure the atomic spacing in certain materials
Diffraction gratings are also used in monochromators:
To specifically analyse a wavelength emitted by molecules in diseased cells from a biopsy sample
To help excite molecules in a sample with a specific wavelength of light
Diffraction gratings are used to select the optimum wavelength of light for use in an optical fibre

Diffraction gratings are most commonly used in spectrometers. These devices play a crucial role in areas of physics such as atomic physics and astrophysics
Examiner Tips and Tricks
Note that while you will be expected to know some applications of diffraction gratings, you will not be tested on specific apparatus or techniques such as spectrometry. When describing the use of spectrometers, avoiding using vague terms such as observe spectra’, ‘spectroscopy’, ‘view absorption / emission spectrum’, ‘compare spectra’, ‘look at light from stars’.

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
