Young's Double-Slit Experiment (AQA AS Physics) : Revision Note
Double Slit Interference
Young's double-slit experiment produces a diffraction and an interference pattern using either:
The interference of two coherent wave sources
A single wave source passing through a double slit
In this typical set-up for Young's double slit experiment:
The laser light source is placed behind the single slit
So the light is diffracted, producing two light sources at slits A and B
The light from the double slits is then diffracted, producing a diffraction pattern made up of bright and dark fringes on a screen
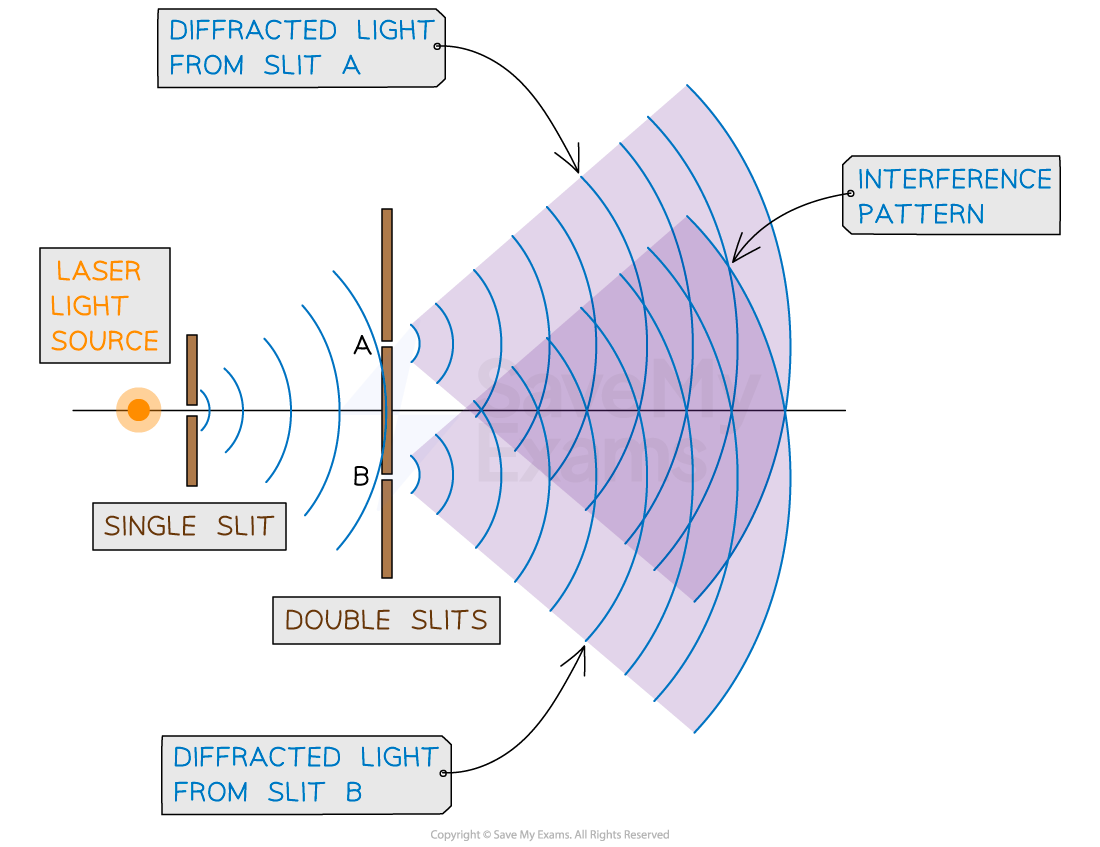
The typical arrangement of Young's double-slit experiment
Diffraction Pattern
The diffraction pattern from the interference of the two sources can be seen on the screen when it is placed far away
Constructive interference between light rays forms bright strips, also called fringes, interference fringes or maxima, on the screen
Destructive interference forms dark strips, also called dark fringes or minima, on the screen
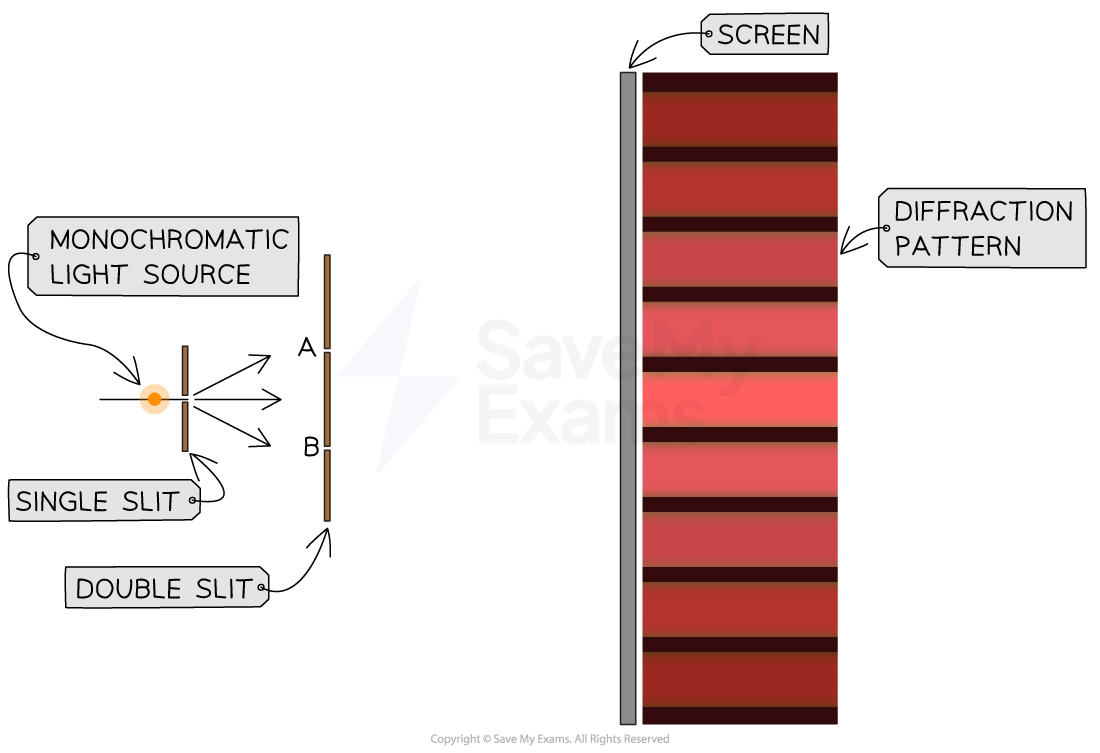
Young's double slit experiment and the resulting diffraction pattern
Each bright fringe is identical and has the same width and intensity
The fringes are all separated by dark narrow bands of destructive interference
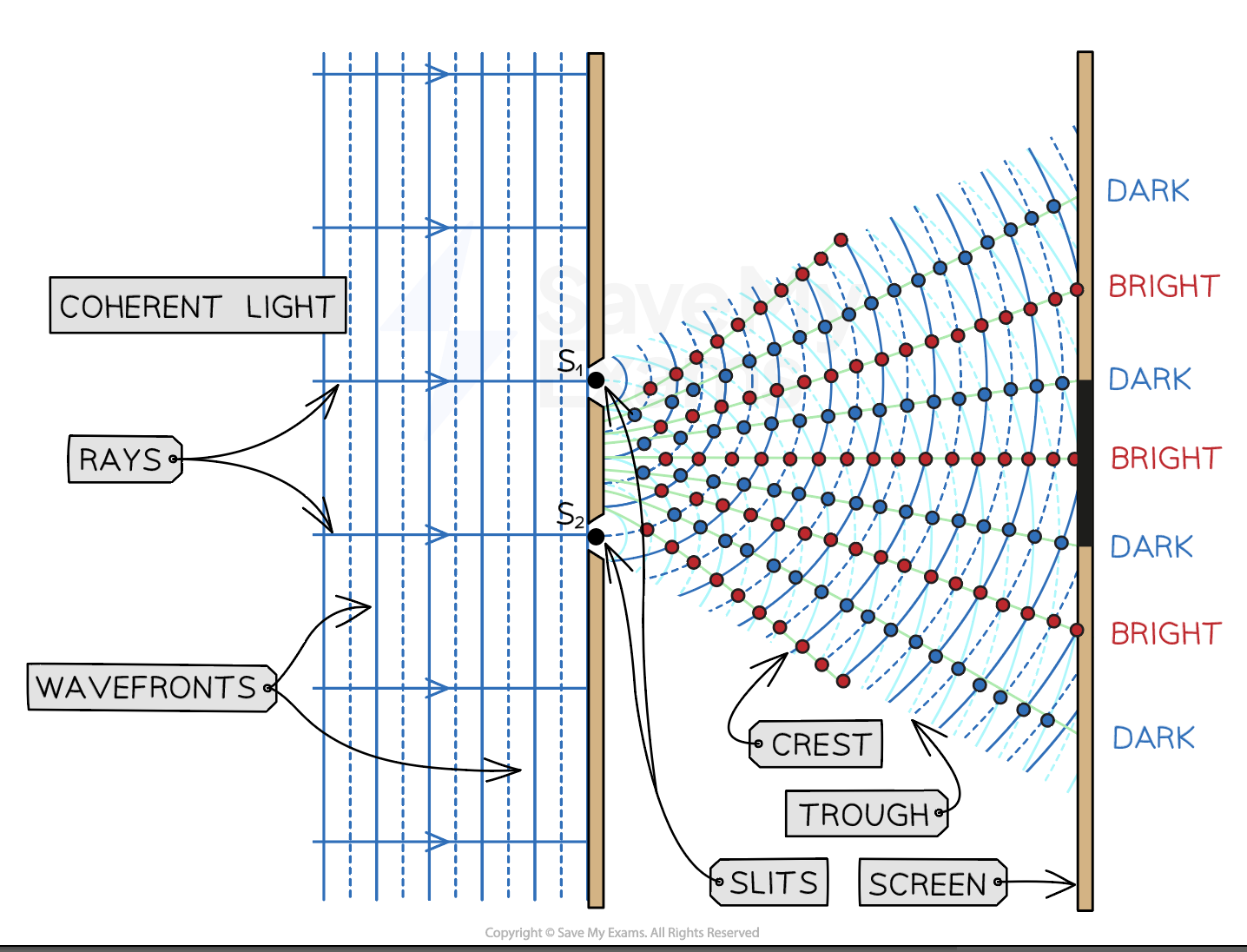
The constructive and destructive interference of laser light through a double slit creates bright and dark strips called fringes on a screen placed far away
Interference Pattern
The Young's double slit interference pattern shows the regions of constructive and destructive interference:
Each bright fringe is a peak of equal maximum intensity
Each dark fringe is a a trough or minimum of zero intensity
The maxima are formed by the constructive interference of light
The minima are formed by the destructive interference of light
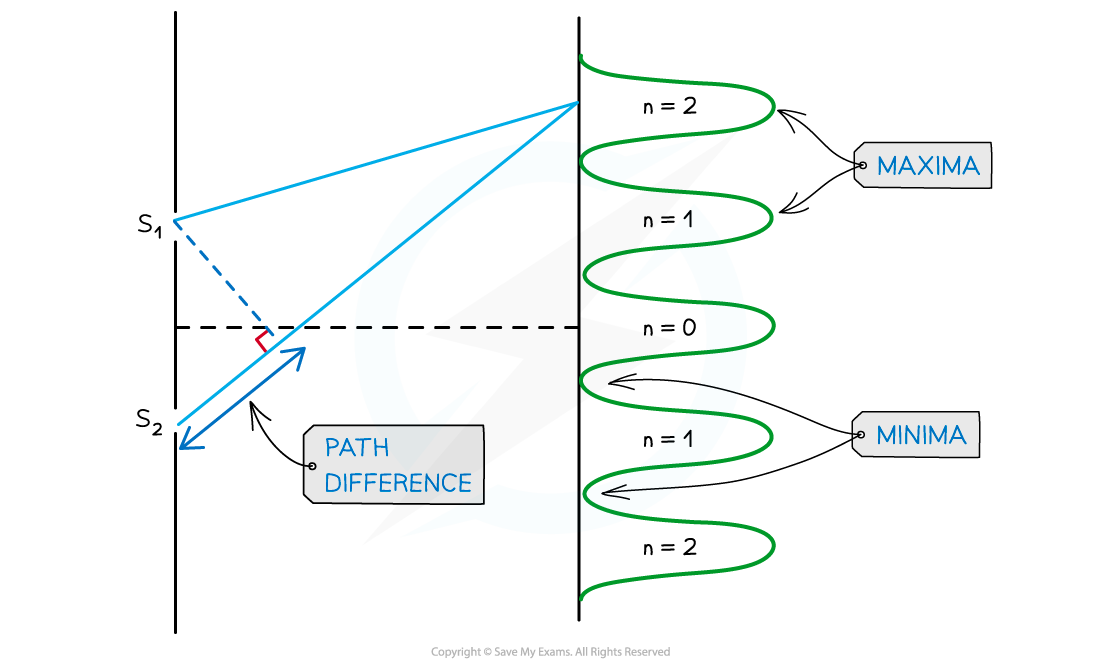
The interference pattern of Young's double-slit diffraction of light
When two waves interfere, the resultant wave depends on the path difference between the two waves
The wave from slit S2 has to travel slightly further than that from S1 to reach the same point on the screen
This extra distance is the path difference
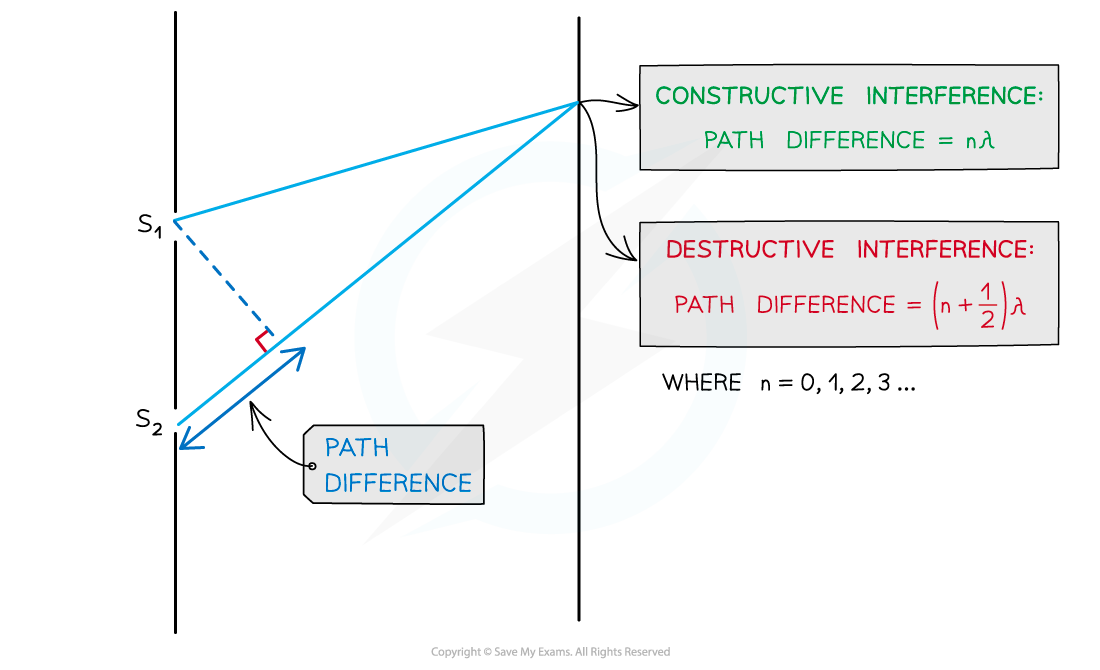
The path difference between two waves is determined by the number of wavelengths that cover their difference in length
Remember:
For constructive interference (or maxima), the difference in wavelengths will be an integer number of whole wavelengths
For destructive interference (or minima) it will be an integer number of whole wavelengths plus a half wavelength
For the maximum in the interference pattern:
There is usually more than one produced
n is the order of the maxima or minima; which represents the position of the maxima away from the central maximum
n = 0 is the central maximum
n = 1 represents the first maximum on either side of the central, n = 2 the next one along....
Worked Example
Two coherent sources of sound waves S1 and S2 are situated 65 cm apart in air as shown below.
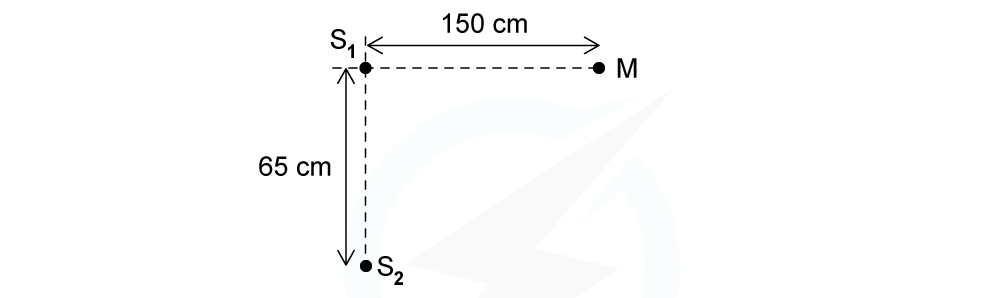
The two sources vibrate in phase but have different amplitudes of vibration. A microphone M is situated 150 cm from S1 along the line normal to S1 and S2. The microphone detects maxima and minima of the intensity of the sound. The wavelength of the sound from S1 to S2 is decreased by increasing the frequency.
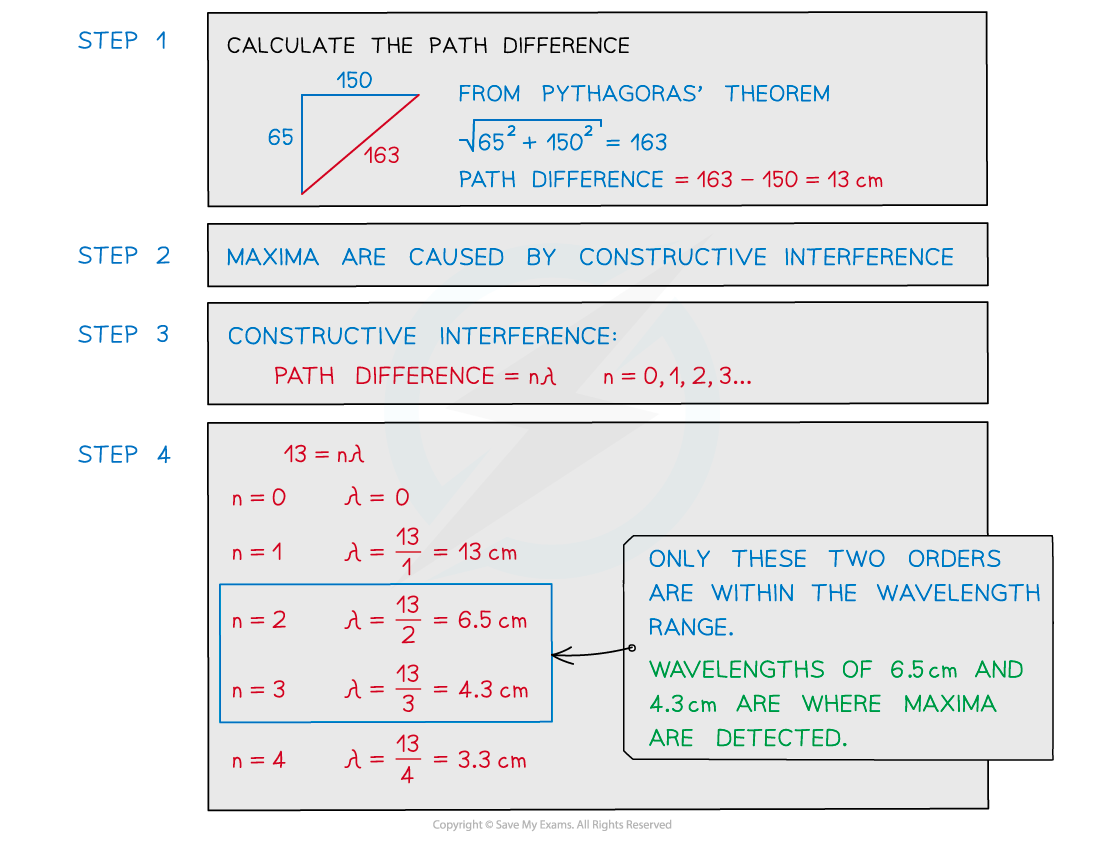
Determine which orders of maxima are detected at M as the wavelength is increased from 3.5 cm to 12.5 cm.
Answer:
Examiner Tips and Tricks
The path difference is more specifically how much longer, or shorter, one path is than the other. In other words, the difference in the distances. Make sure not to confuse this with the distance between the two paths.
Fringe Spacing Equation
The spacing between the bright or dark fringes in the diffraction pattern formed on the screen can be calculated using the double slit equation:
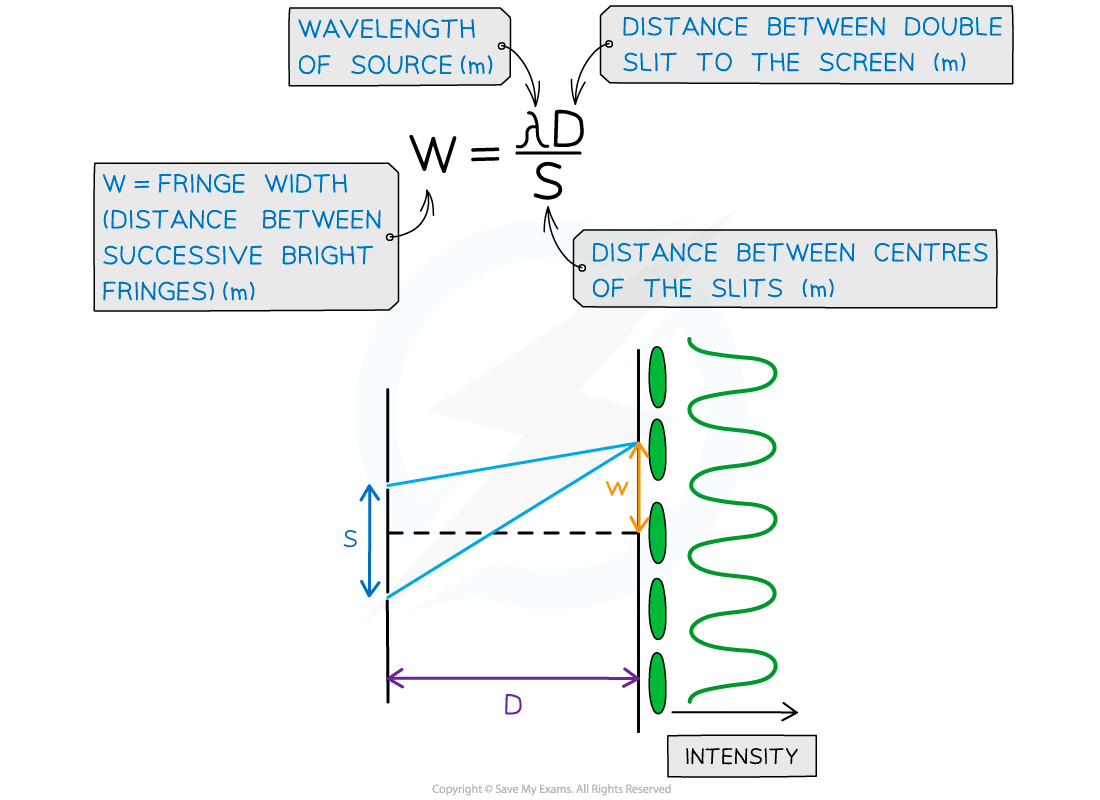
Double slit interference equation with w, s and D represented on a diagram
In this experiment:
D is much bigger than any other dimension, normally several metres long
s is the separation between the two slits and is often the smallest dimension, normally in mm
w is the distance between the fringes on the screen, often in cm. This can be obtained by measuring the distance between the centre of each consecutive bright spot.
The above equation shows that the separation between the fringes will increase if:
The wavelength, λ of the incident light increases
The distance, s between the screen and the slits increases
The separation, w between the slits decreases
Worked Example
A laser is placed in front of a double-slit as shown in the diagram below.
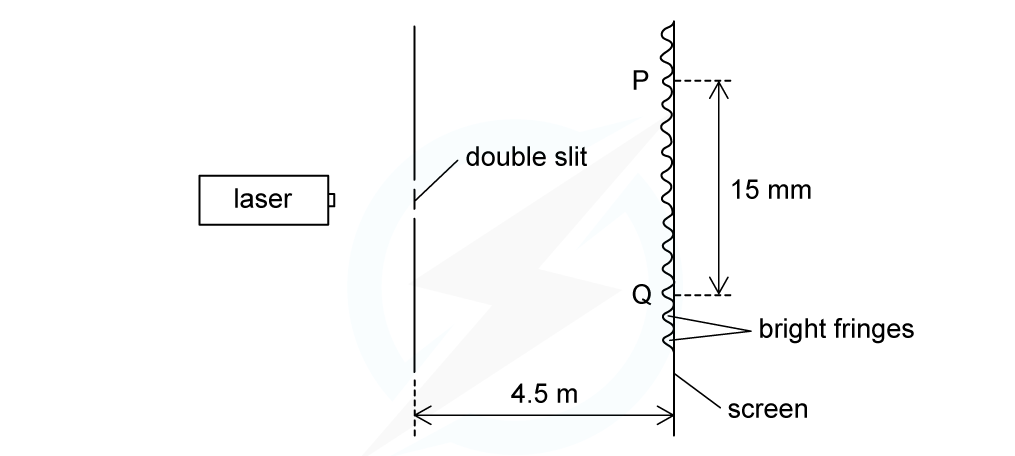
The laser emits light of frequency 750 THz. The separation of the maxima P and Q observed on the screen is 15 mm. The distance between the double slit and the screen is 4.5 m.
Calculate the separation of the two slits.
Answer:

Examiner Tips and Tricks
Since w, s and D are all distances, it's easy to mix up which they refer to. Labelling the double-slit diagram with each of these quantities can help ensure you don't use the wrong variable for a quantity.
Interference Patterns
A source of white light diffracted through a double slit will produce the following diffraction pattern
It is different to that produced by a single slit or a diffraction grating
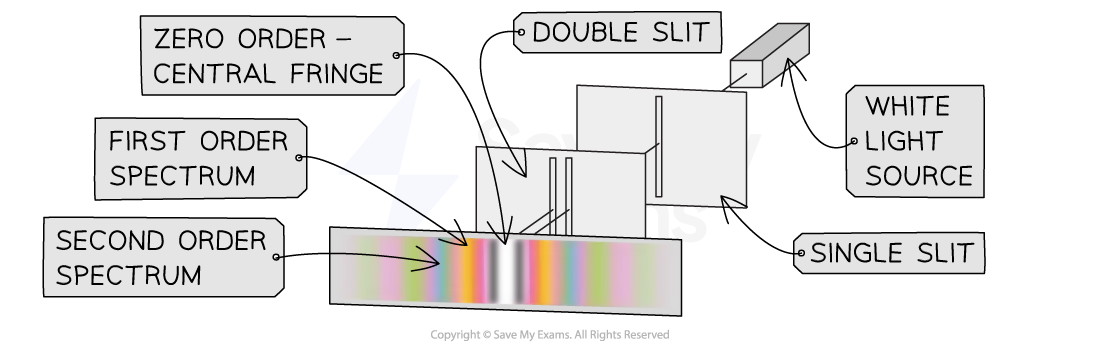
The interference pattern produced when white light is diffracted through a double slit
Each maximum is of roughly equal width
The central maximum is white because each wavelength interferes here constructively
There are two dark narrow destructive interference fringes on either side
All other maxima are composed of a spectrum
Separate diffraction patterns can be observed for each wavelength of light
The shortest wavelength (violet / blue) would appear nearest to the central maximum because it is diffracted the least
The longest wavelength (red) would appear furthest from the central maximum because it is diffracted the most
The colours look blurry and further away from the central maximum, the fringe spacing gets so small that the spectra eventually merge without any space between them
As the maxima move further away from the central maximum, the wavelengths of blue observed decrease and the wavelengths of red observed increase

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
