Path Difference & Coherence (AQA AS Physics)

Superposition and Interference

• When two or more waves arrive at the same point and overlap, their amplitudes combine  
  • This is called superposition
• The principle of superposition states that:

When two or more waves overlap at a point, the displacement at that point is equal to the sum of the displacements of the individual waves

• The superposition of surface water waves shows the effect of this overlap
  • There are areas of zero displacement, where the water is flat
  • There are areas of increased displacement, where the water waves are higher

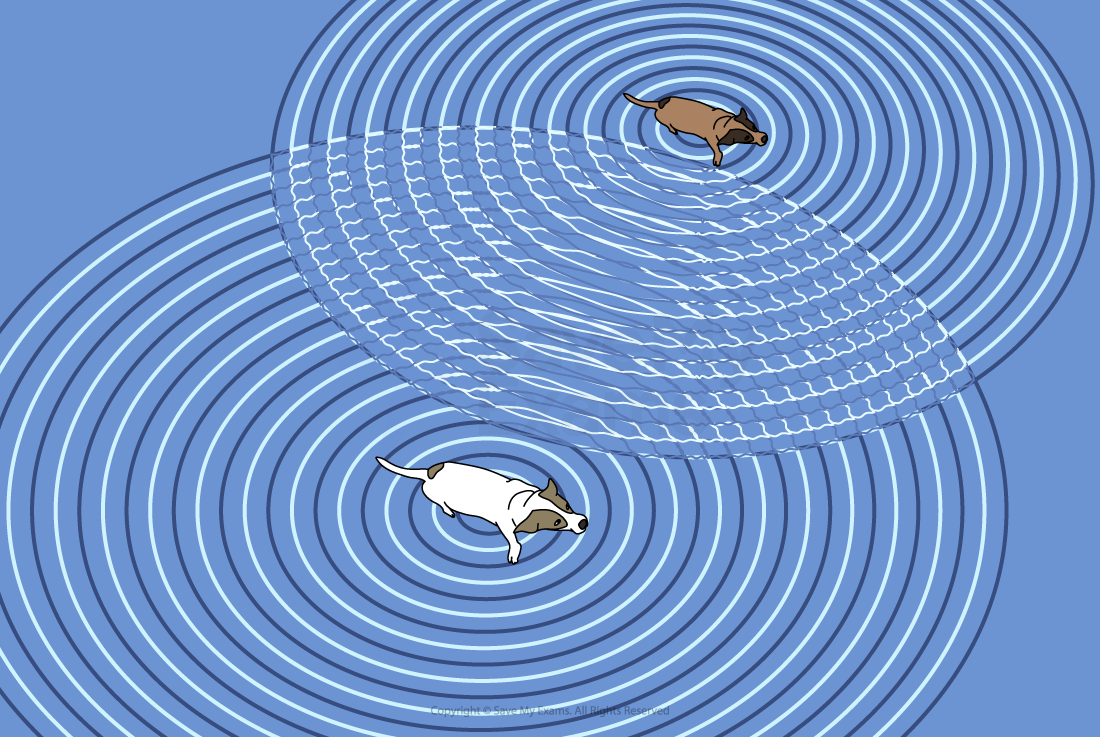
The dogs make waves in the water which superimpose to give areas of both zero and increased displacement.

• It is possible to analyse superposition clearly when the waves are drawn on a vertical displacement (amplitude)-displacement graph

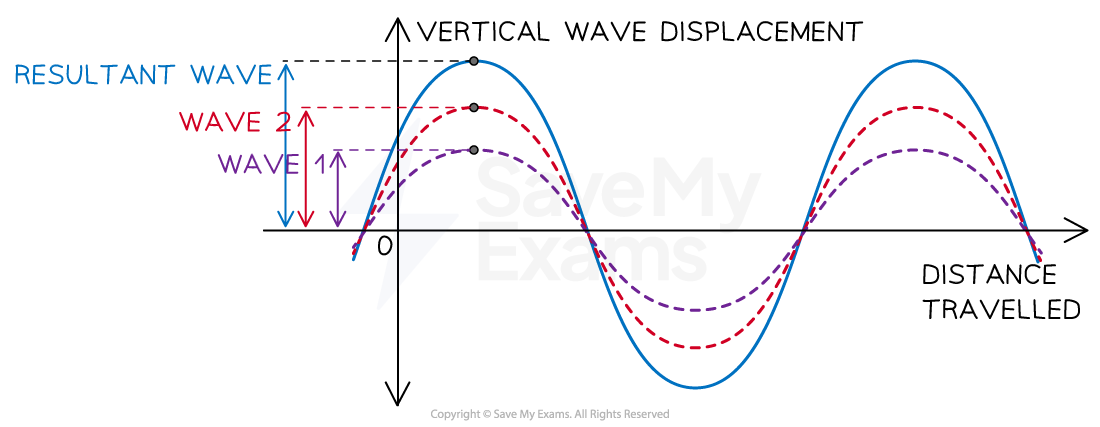
Waves can superimpose so their amplitudes are added together often creating a larger resultant amplitude

• Interference is the effect of this superposition
  • Interference can be seen clearly when waves overlap in phase or antiphase 
• When two waves are in antiphase, their combined effect means they cancel each other out
  • This is known as destructive interference
• When two waves are in phase, their combined effect makes the resultant wave amplitude larger
  • This is known as constructive interference.

 

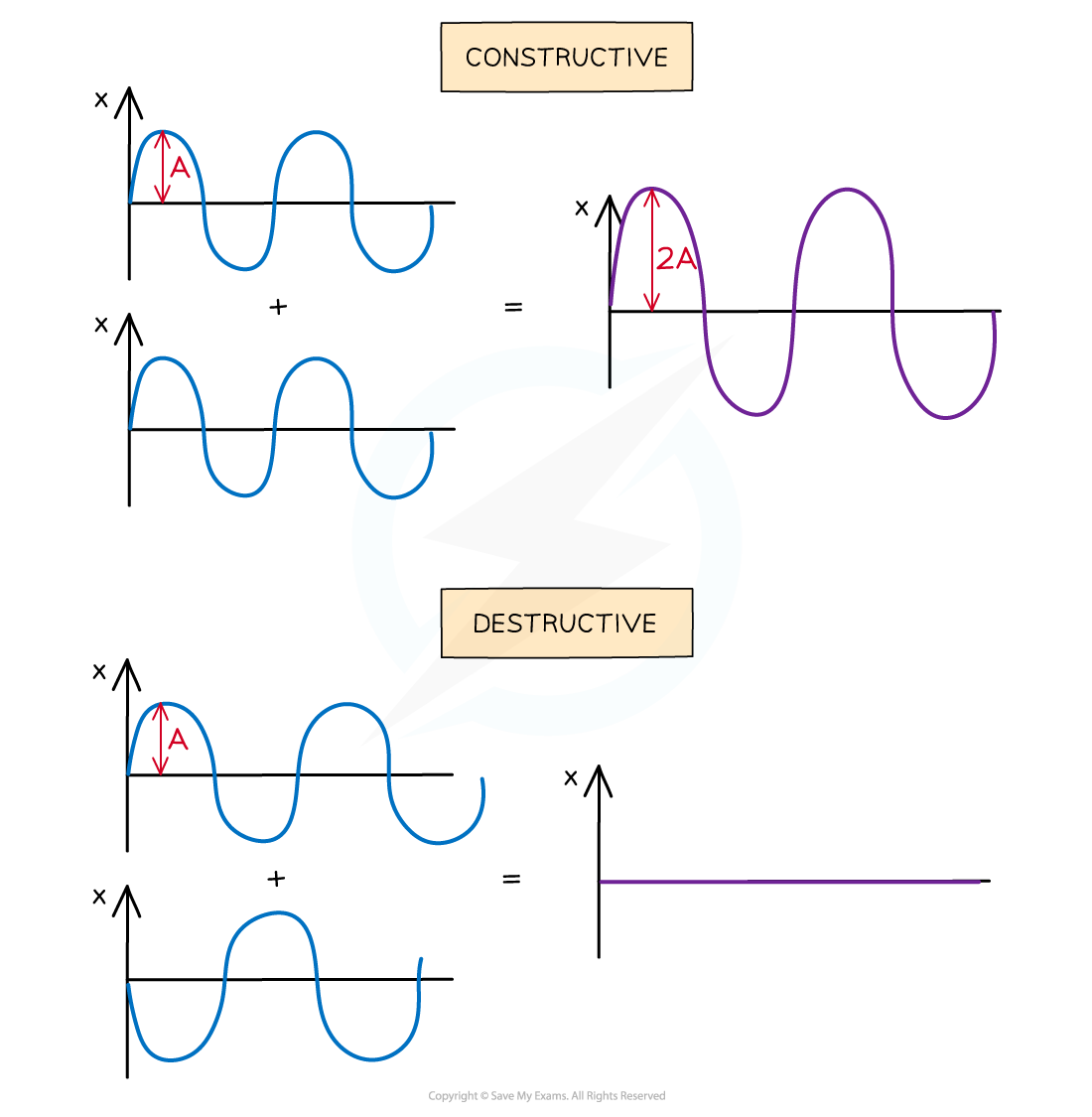
• At points where two waves are neither in phase nor in antiphase, the resultant amplitude is somewhere in between the two extremes
• Individual wave displacements may be positive or negative and are combined in the same way as other vector quantities

Coherence

• For waves to undergo constructive and destructive interference, they must be coherent
• Coherence occurs when waves have:
  • The same frequency
  • A constant phase difference

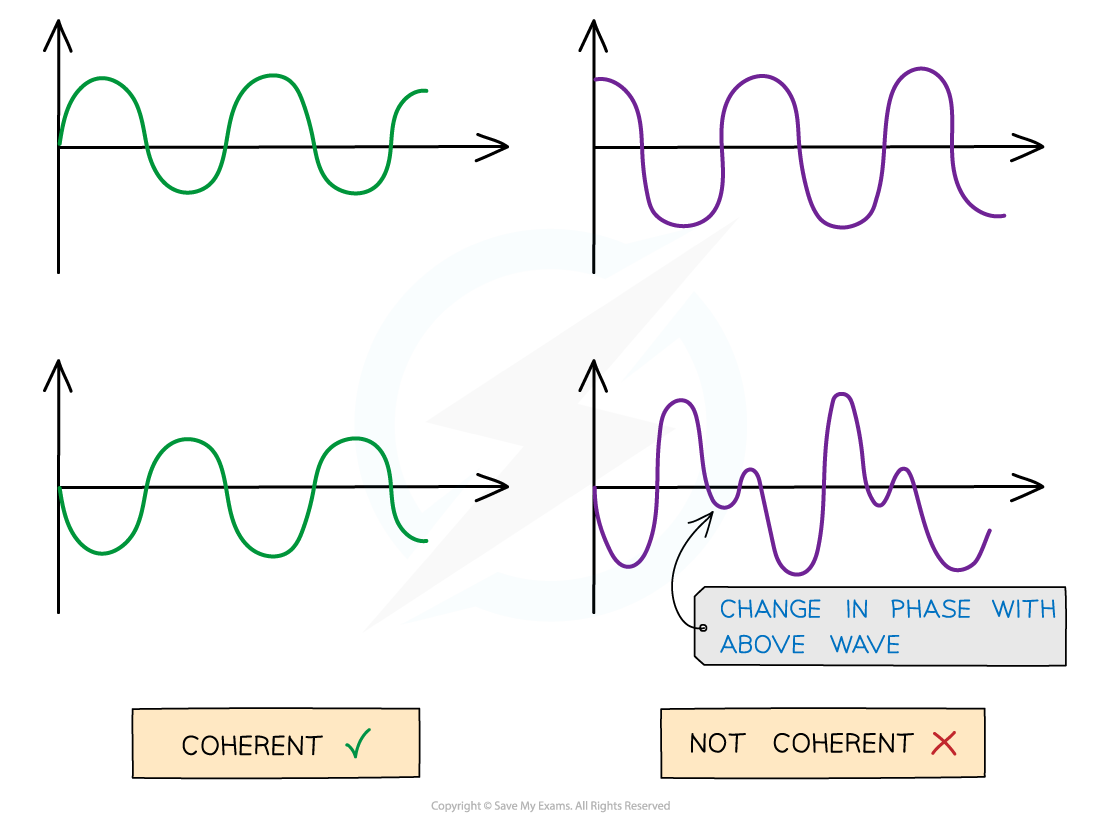
Coherent vs. non-coherent waves. The abrupt change in phase creates an inconsistent phase difference.

• Examples of interference from coherent light sources are:  
  • Monochromatic laser light 
  • Sound waves from two nearby speakers emitting sound of the same frequency

Path Difference

• Path difference is defined as:

The difference in distance travelled by two waves from their sources to the point where they meet

• Path difference vs phase difference
  • Path difference compares the amount of progress made by waves along a path 
  • Phase difference compares the distance between the phases (peaks and troughs) of coherent waves that are normally travelling parallel to each other at a point 
• The path difference between two coherent waves determines whether there is constructive or destructive interference where they meet

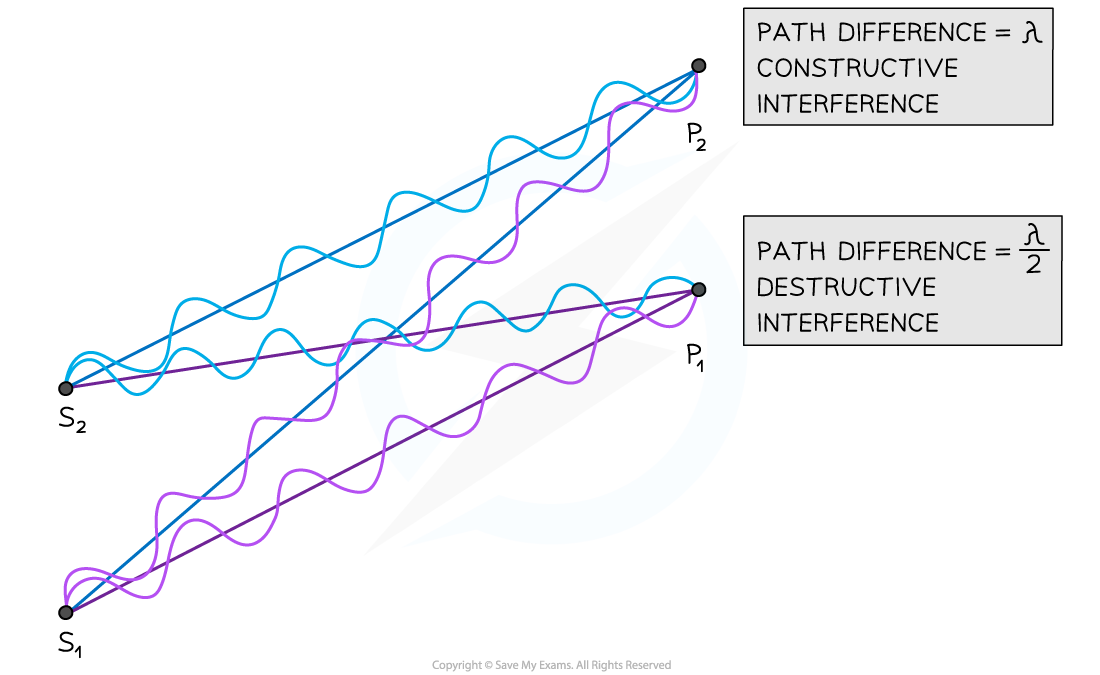
At point P₂ the waves from S₁ and S₂ have a path difference of a whole number of wavelengths resulting in constructive interference. At point P₁ the waves have a path difference of an odd number of half wavelengths resulting in destructive interference 

• Path difference is generally expressed in multiples of wavelength
  • Remember to count a whole number of wavelengths (the wave should go up, down and then back to where it started in one wavelength)
• In the diagram above, the number of wavelengths between:
  • S₁ ➜ P₁ = 6λ
  • S₂ ➜ P₁ = 6.5λ
  • S₁ ➜ P₂ = 7λ
  • S₂ ➜ P₂ = 6λ

• The path difference at point P₁ is 6.5λ – 6λ = λ / 2
• The path difference at point P₂ is 7λ – 6λ = λ

Conditions for Constructive and Destructive Interference

• In general, for waves emitted by two coherent sources very close together:
• The condition for constructive interference is:

path difference = 

• The condition for destructive interference is:

path difference =

• Where:
  • λ = wavelength of the waves in metres (m)
  • n = 0, 1, 2, 3... (any other integer)

Wavefront Diagrams

• Wave behaviour can also be shown by a wavefront diagram
• A curved line represents each wavefront (peak or trough)
• This can show the interference between waves more clearly

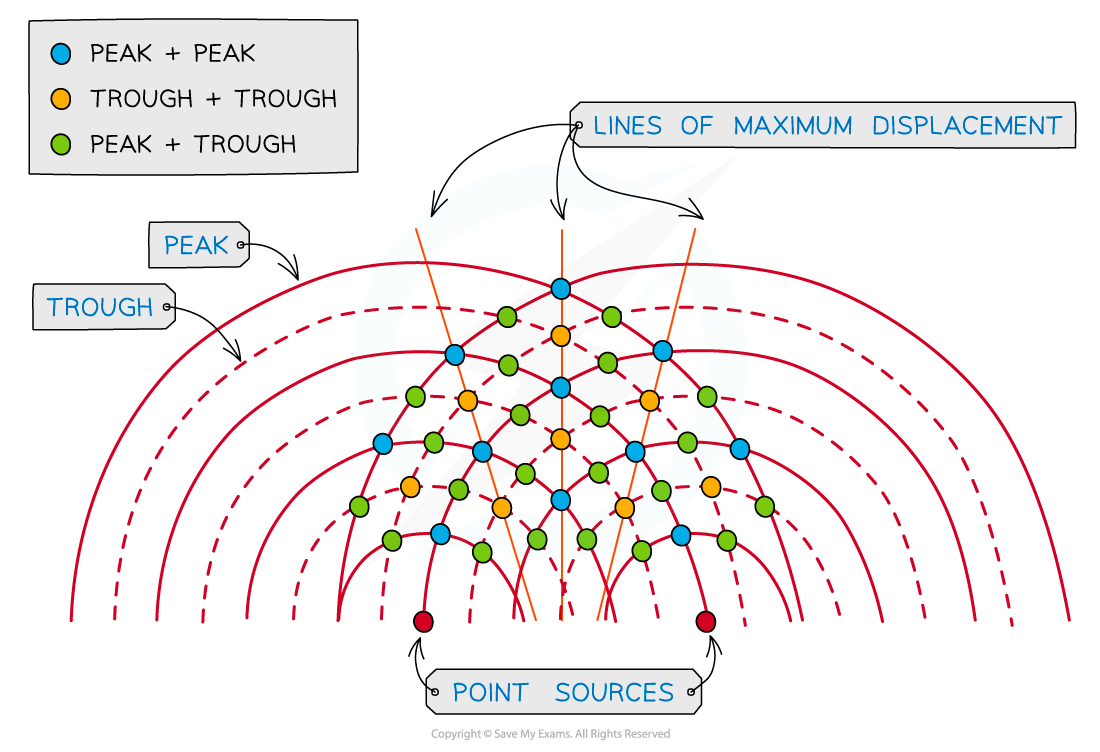
At the blue dot where the peak of two waves meet, constructive interference occurs. At the yellow dot where two troughs meet, constructive interference also occurs. Constructive interference occurs along the lines of maximum displacement. At the green dot, where a peak and a trough meet, destructive interference occurs

• On a wavefront diagram, it is possible to count the number of wavelengths to determine whether constructive or destructive interference occurs at a certain point

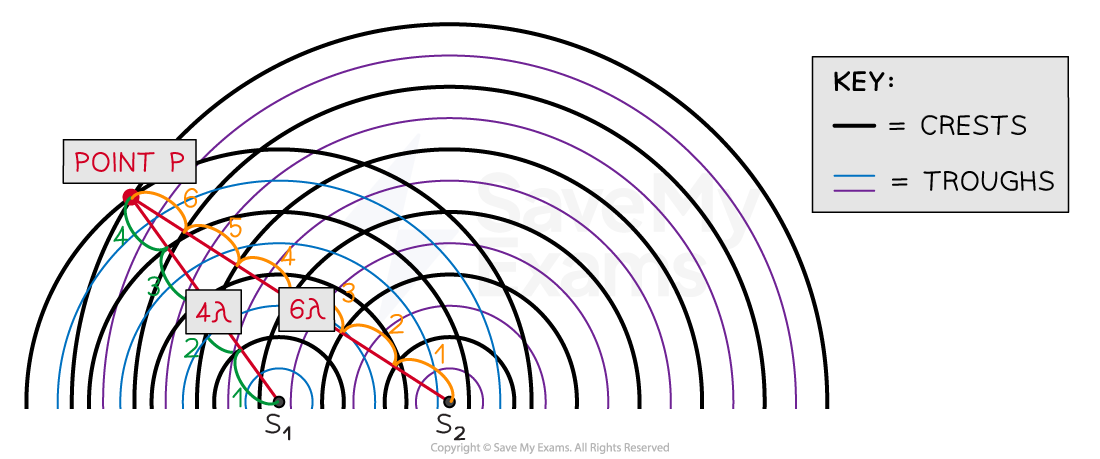
At point P the waves from S₁ and S₂ have a path difference of a whole number of wavelengths, resulting in constructive interference

• At point P, the number of crests from:
  • Source S₁ = 4λ
  • Source S₂ = 6λ

• So the path difference at P is 6λ – 4λ = 2λ
• This is a whole number of wavelengths, hence, constructive interference occurs at point P

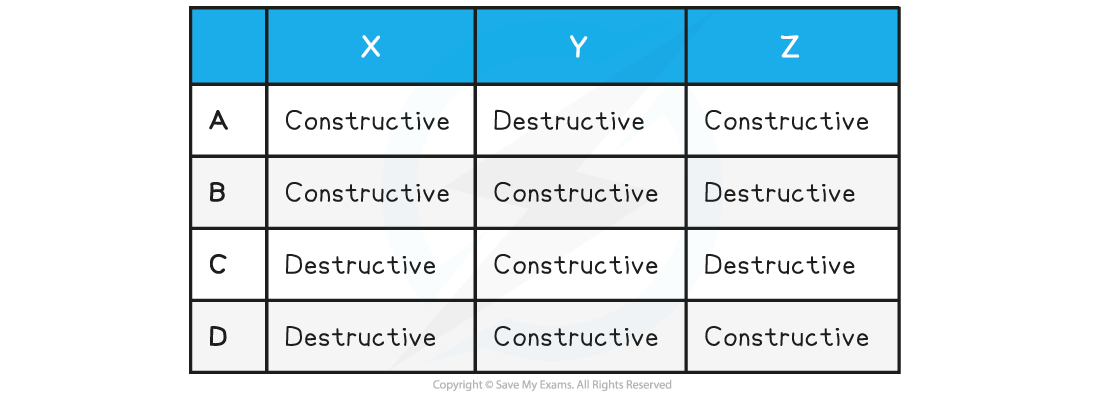
      ANSWER: B

• At point X:
  • Both peaks of the waves are overlapping
  • Path difference = 5.5λ – 4.5λ = λ
  • This is constructive interference and rules out options C and D

• At point Y:
  • Both troughs are overlapping
  • Path difference = 3.75λ – 3.75λ = 0
  • Therefore constructive interference occurs

• At point Z:
  • A peak of one of the waves meets the trough of the other
  • Path difference = 4λ – 3.5λ = λ / 2
  • This is destructive interference