Harmonics (AQA AS Physics)

• Stationary waves can have different wave patterns, known as harmonics
  • These depend on the frequency of the vibration and the situation in which they are created

• These harmonics can be observed on a string with two fixed ends
• As the frequency is increased, more harmonics begin to appear

Harmonics on a String

• When a stationary wave, such as a vibrating string, is fixed at both ends, the simplest wave pattern is a single loop made up of two nodes and an antinode
  • This is called the first harmonic or fundamental frequency

• The particular frequencies (i.e. resonant frequencies) of stationary waves formed depend on the length of the string L and the wave speed v
• The frequencies can be calculated from the string length and wave equation
• For a string of length L, the wavelength of the lowest harmonic is 2L
  • This is because there is only one loop of the stationary wave, which is a half wavelength

• Therefore, the frequency is equal to:

• The second harmonic has three nodes and two antinodes
• The wavelength is L and the frequency is equal to:

• The third harmonic has four nodes and three antinodes
• The wavelength is 2L / 3 and the frequency is equal to:

• The nth harmonic has n antinodes and n + 1 nodes
• The wavelengths and frequencies of the first three harmonics can be summarised as follows:

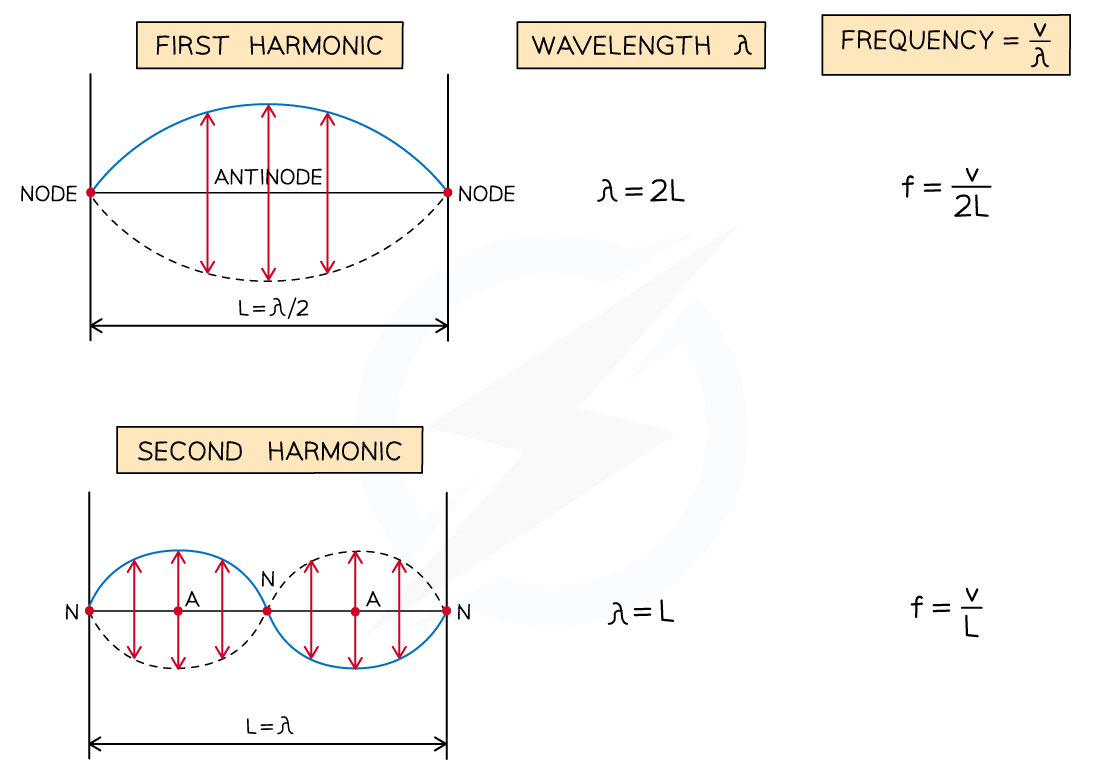
Diagram showing the first three modes of vibration of a stretched string with corresponding frequencies

• If you look carefully at the equations for frequency for the first, second and third harmonics then you will notice that for the

nth harmonic the frequency = n × frequency of first harmonic

Step 1: Calculate the frequency of the first harmonic

f₃ = 3 f₁

f₁ = f₃ ÷ 3 = 150 ÷ 3 = 50 Hz

Step 2: Calculate the frequency of the fifth harmonic

f₅ = 5 f₁

f₅ = 5 × 50 = 250 Hz

• The speed of a wave travelling along a string with two fixed ends is given by:

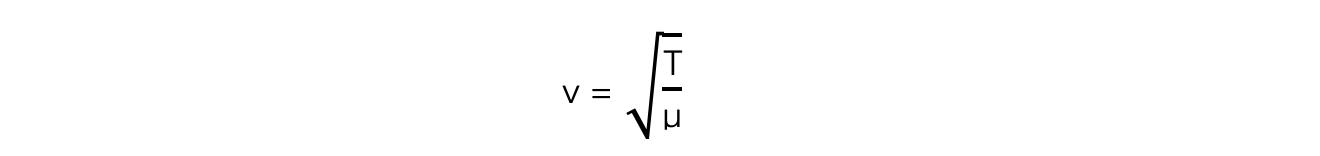
• Where:
  • T = tension in the string (N)
  • μ = mass per unit length of the string (kg m^–1)

• For the first harmonic of a stationary wave of length L, the wavelength, λ = 2L
• Therefore, according to the wave equation, the speed of the stationary wave is:

v = fλ = f × 2L

• Combining these two equations leads to the frequency of the first harmonic:

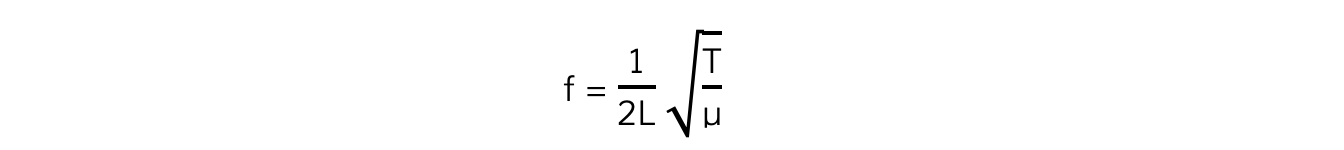
• Where:
  • f = frequency (Hz)
  • L = the length of the string (m)