Calculating Uncertainties (AQA AS Physics)

• There is always a degree of uncertainty when measurements are taken; the uncertainty can be thought of as the difference between the actual reading taken (caused by the equipment or techniques used) and the true value
• Uncertainties are not the same as errors
  • Errors can be thought of as issues with equipment or methodology that cause a reading to be different from the true value
  • The uncertainty is a range of values around a measurement within which the true value is expected to lie, and is an estimate

• For example, if the true value of the mass of a box is 950 g, but a systematic error with a balance gives an actual reading of 952 g, the uncertainty is ±2 g
• These uncertainties can be represented in a number of ways:
  • Absolute Uncertainty: where uncertainty is given as a fixed quantity
  • Fractional Uncertainty: where uncertainty is given as a fraction of the measurement
  • Percentage Uncertainty: where uncertainty is given as a percentage of the measurement

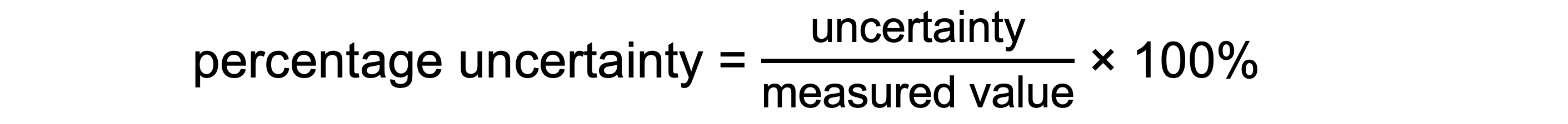
• To find uncertainties in different situations:
• The uncertainty in a reading: ± half the smallest division
• The uncertainty in a measurement: at least ±1 smallest division
• The uncertainty in repeated data: half the range i.e. ± ½ (largest - smallest value)
• The uncertainty in digital readings: ± the last significant digit unless otherwise quoted

How to calculate absolute, fractional and percentage uncertainty

• Always make sure your absolute or percentage uncertainty is to the same number of significant figures as the reading

• When combining uncertainties, the rules are as follows:

Adding / Subtracting Data

• Add together the absolute uncertainties

Multiplying / Dividing Data

• Add the percentage or fractional uncertainties

Raising to a Power

• Multiply the percentage uncertainty by the power

1. Calculate the mean value 

mean ω = = 0.153 rad s^–1

2. Calculate half the range (this is the uncertainty for multiple readings)

× (0.159 – 0.147) = 0.006 rad s^–1

3. Calculate percentage uncertainty

× 100 % = × 100 %

× 100 % = 3.92 %