Estimating Physical Quantities (AQA AS Physics) : Revision Note
Orders of Magnitude
When a number is expressed in an order of 10, this is an order of magnitude.
Example: If a number is described as 3 × 108 then that number is actually 3 × 100 000 000
The order of magnitude of 3 × 108 is just 108
Orders of magnitude follows rules for rounding
The order of magnitude of 6 × 108 is 109 as the magnitude is rounded up
A quantity is an order of magnitude larger than another quantity if it is about ten times larger
Similarly, two orders of magnitude would be 100 times larger, or 102
In physics, orders of magnitude can be very large or very small
When estimating values, it’s best to give the estimate of an order of magnitude to the nearest power of 10
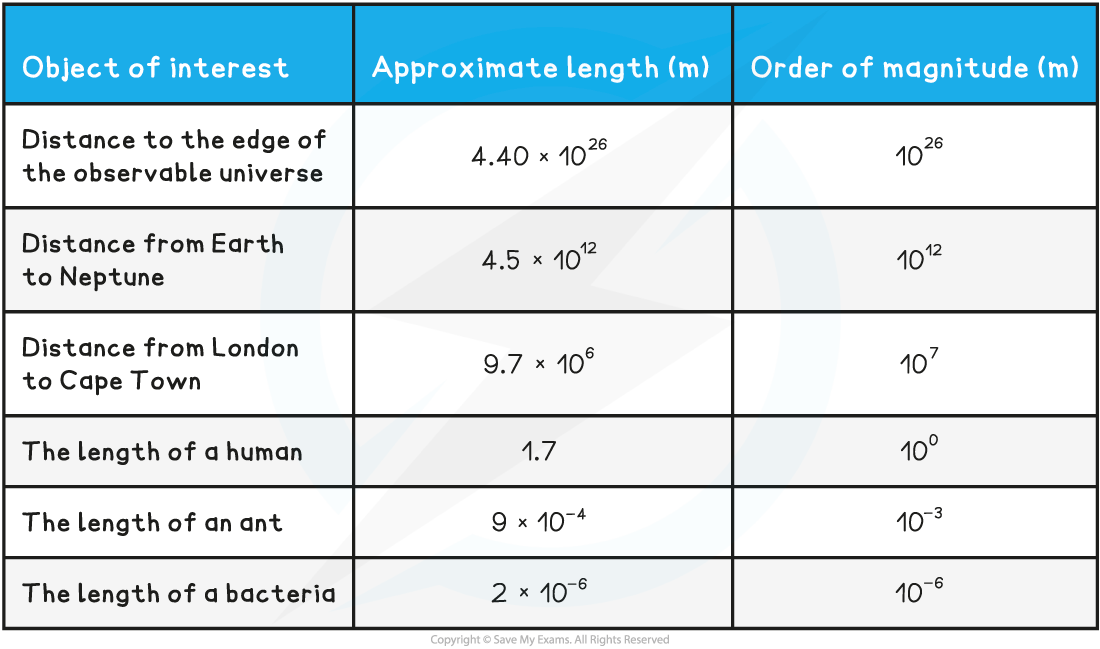
For example, the diameter of the Milky Way is approximately 1 000 000 000 000 000 000 000 m
It is inconvenient to write this many zeros, so it’s best to use scientific notation as follows:
1 000 000 000 000 000 000 000 = 1 × 1021 m
The order of magnitude is 1021
Orders of magnitude make it easier to compare the relative sizes of objects
For example, a quantity with an order of magnitude of 106 is 10 000 times larger than a quantity with a magnitude of 102
Order of Magnitudes Table
Worked Example
Estimate the order of magnitude for the following quantities:
The temperature of the surface of the Sun in Kelvin
The power of a standard lightbulb
The volume of the room you are in now
Answer:
1. The temperature of the surface of the Sun in Kelvin
The temperature of the surface of the Sun is about 6000 K
This is an order of magnitude of ~ 104 K
2. The power of a standard lightbulb
The power of a standard lightbulb is about 60 W
This is an order of magnitude of ~ 102 W
3. The volume of the room you are in now
This depends on the room you are in
The shape should roughly be cubic or (rectangular) cuboid
Volume = length × width × height
For a cubic room with length 3 m, volume = 33 = 27 m3
This is an order of magnitude of ~ 10 m3
Estimating Physical Quantities
There are important physical quantities to learn in physics
It is useful to know these physical quantities, they are particularly useful when making estimates
A few examples of useful quantities to memorise are given in the table below (this is by no means an exhaustive list)
Estimating Physical Quantities Table

Worked Example
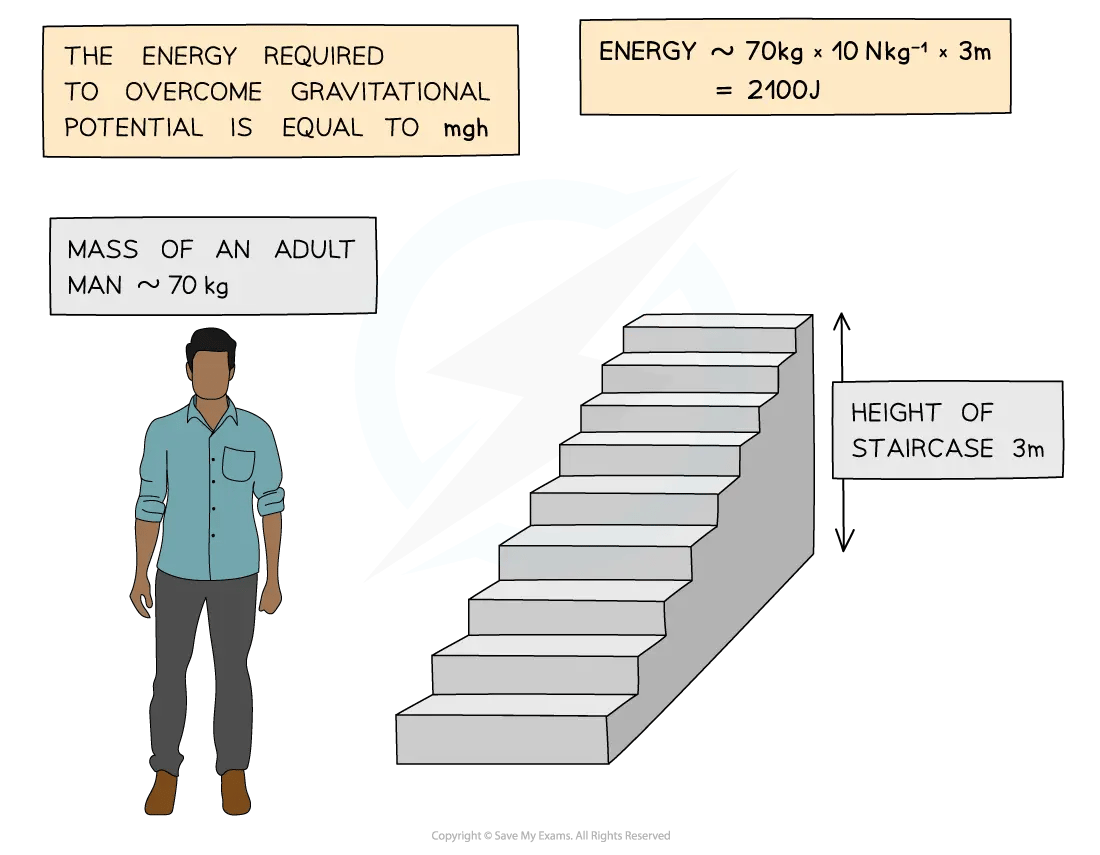
Estimate the energy required for an adult man to walk up a flight of stairs.
Answer:

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?

