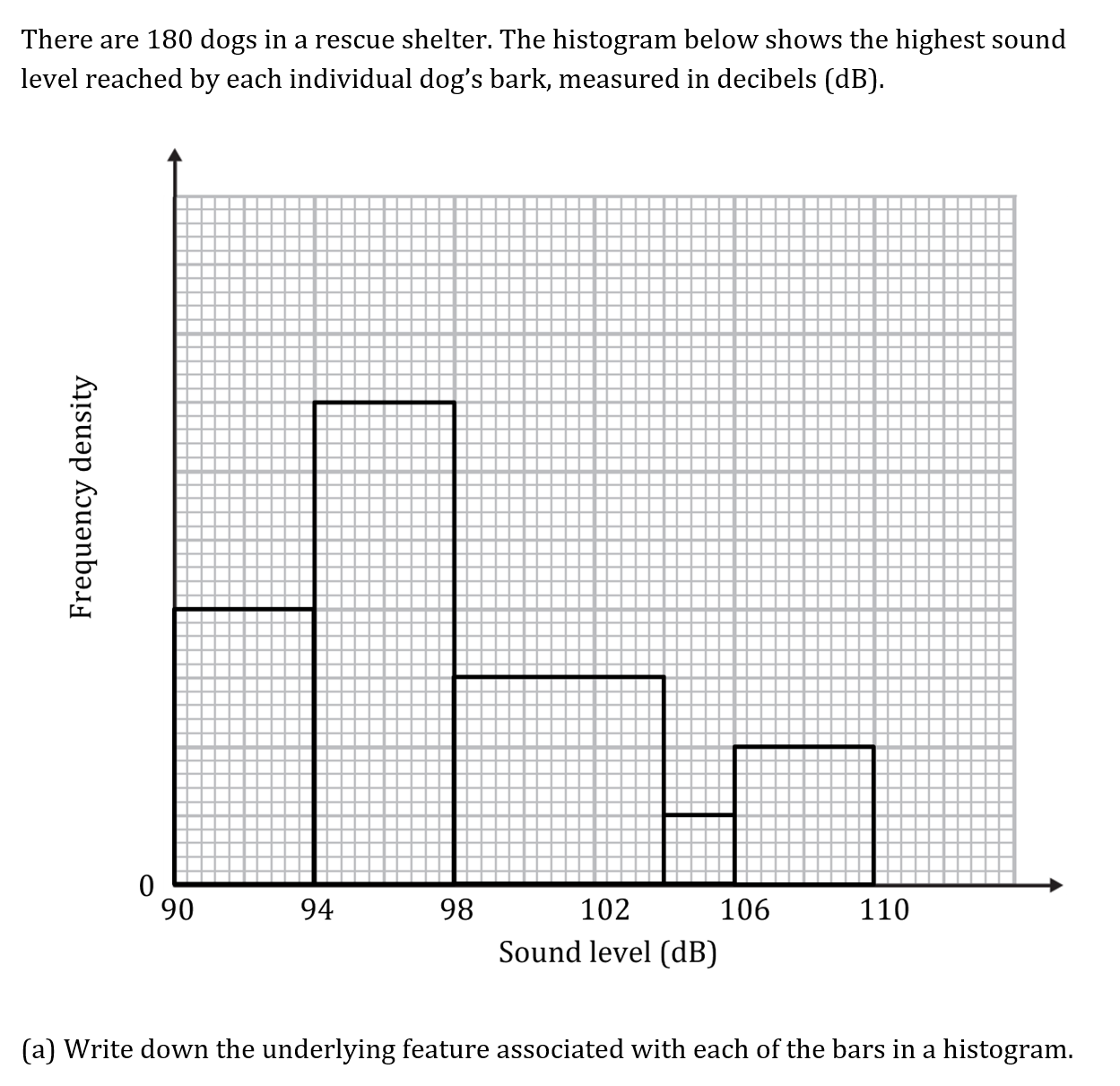
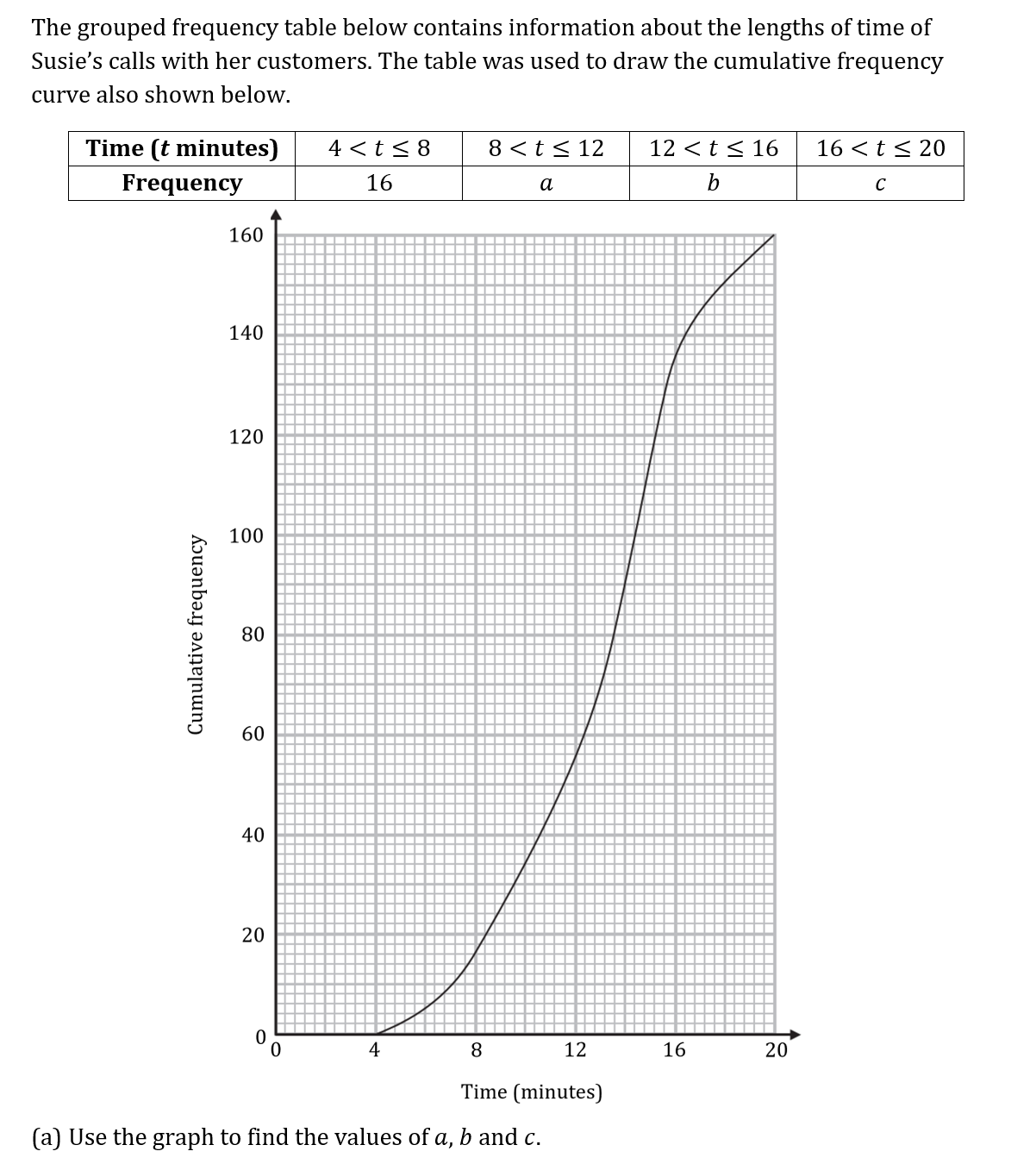
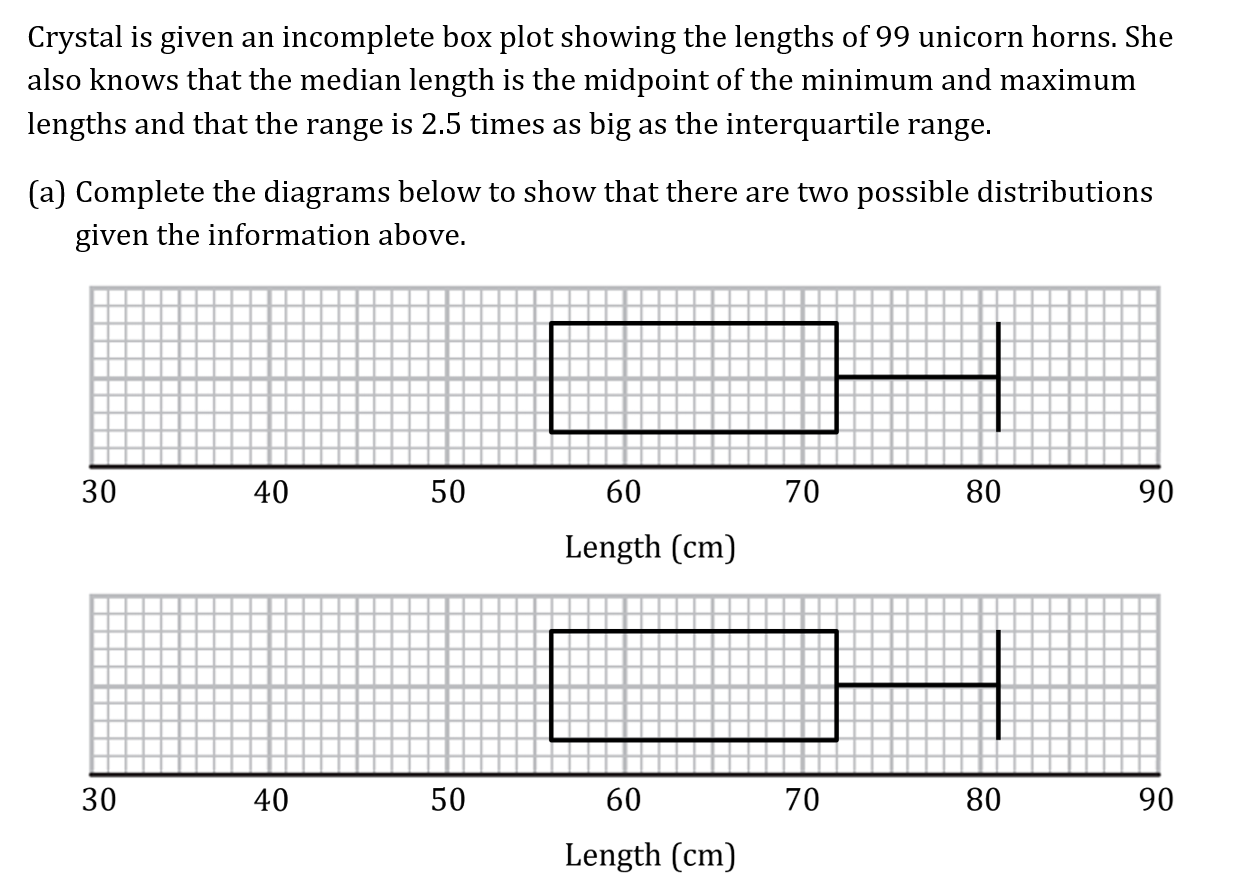
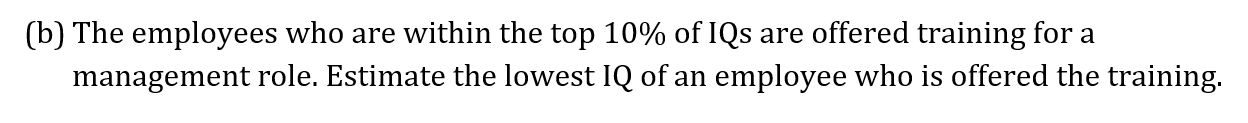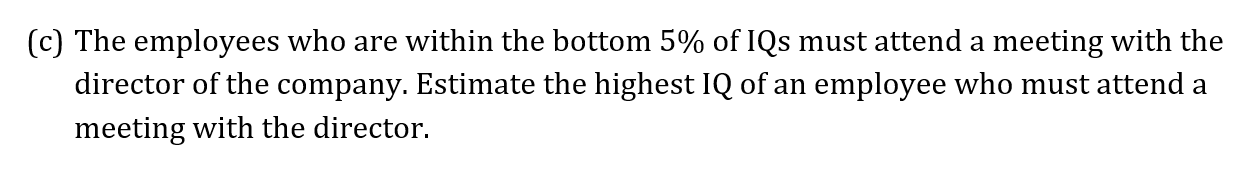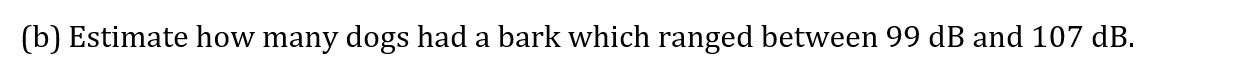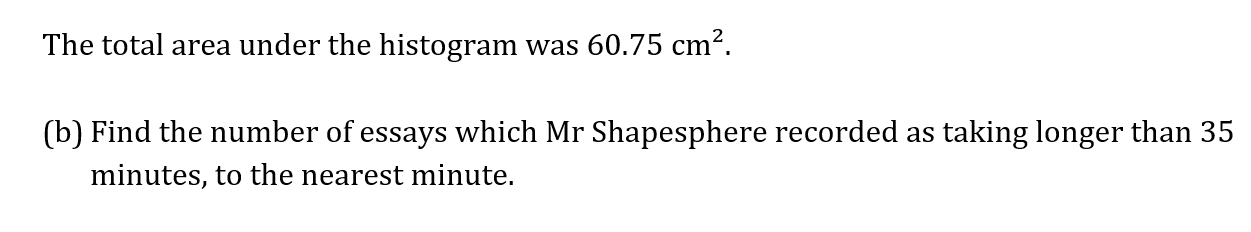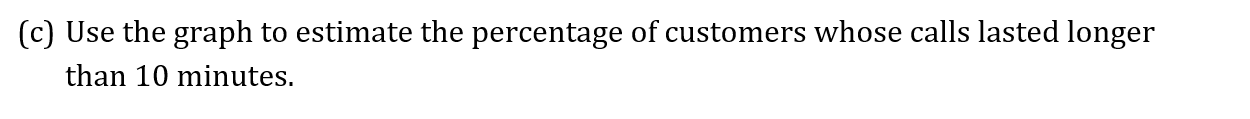The train journey times, in minutes, between March and Peterborough, are illustrated in the box and whisker diagram below.
Using the box and whisker diagram above to find
The above times show those for a weekday. The table below summarises the times for the same journey on a Saturday.
|
|
Journey Time |
|
Fastest |
16 |
|
Lower quartile |
18 |
|
Median |
19 |
|
Upper Quartile |
20 |
|
Slowest |
25 |
On the grid, draw a box plot for the information given in the table.

Did this page help you?