Increasing & Decreasing Functions (AQA AS Maths): Revision Note

Increasing & Decreasing Functions

What are increasing and decreasing functions?

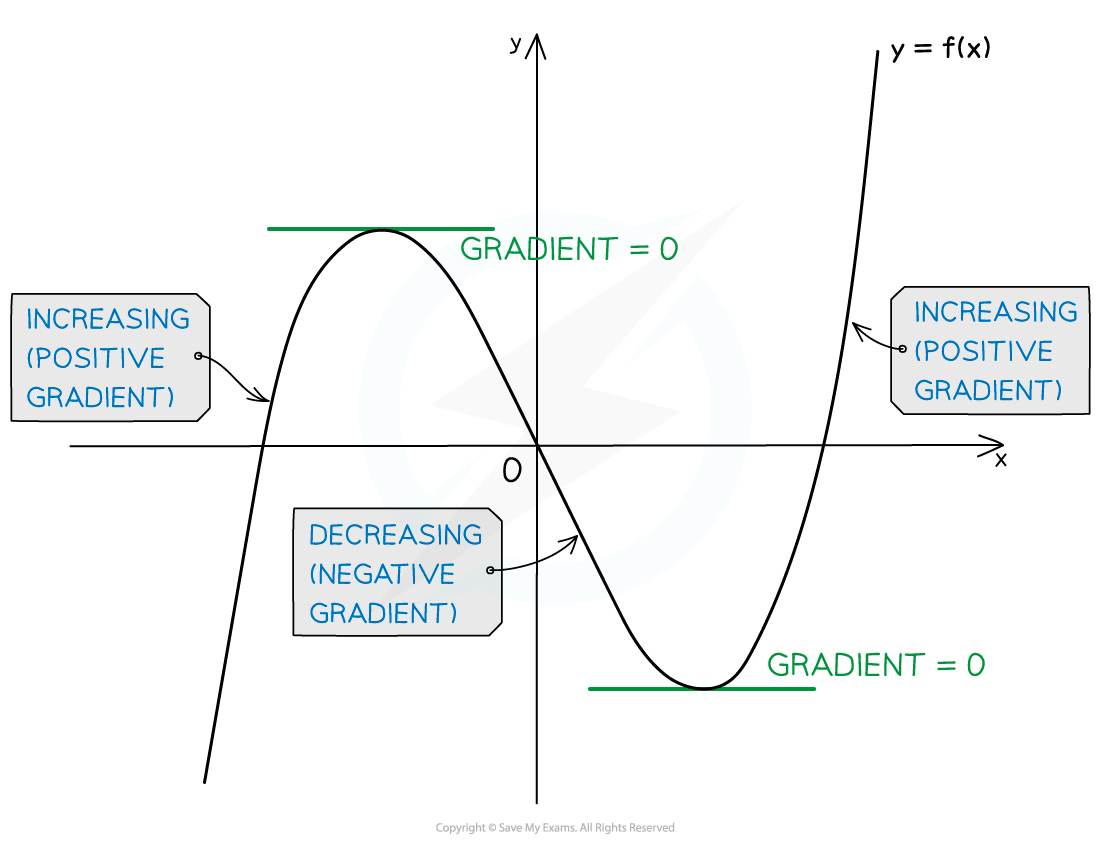
• A function f(x) is increasing on an interval [a, b] if f'(x) ≥ 0 for all values of x such that a< x < b.

  • If f'(x) > 0 for all x values in the interval then the function is said to be strictly increasing

  • In most cases, on an increasing interval the graph of a function goes up as x increases

• A function f(x) is decreasing on an interval [a, b] if f'(x) ≤ 0 for all values of x such that a < x < b

  • If f'(x) < 0 for all x values in the interval then the function is said to be strictly decreasing

  • In most cases, on a decreasing interval the graph of a function goes down as x increases

• To identify the intervals on which a function is increasing or decreasing you need to:

1. Find the derivative f'(x)

2. Solve the inequalities f'(x) ≥ 0 (for increasing intervals) and/or f'(x) ≤ 0 (for decreasing intervals)