Gradients, Tangents & Normals (AQA AS Maths): Revision Note

Gradients, Tangents & Normals

Using the derivative to find the gradient of a curve

• To find the gradient of a curve y= f(x) at any point on the curve, substitute the x‑coordinate of the point into the derivative f'(x)

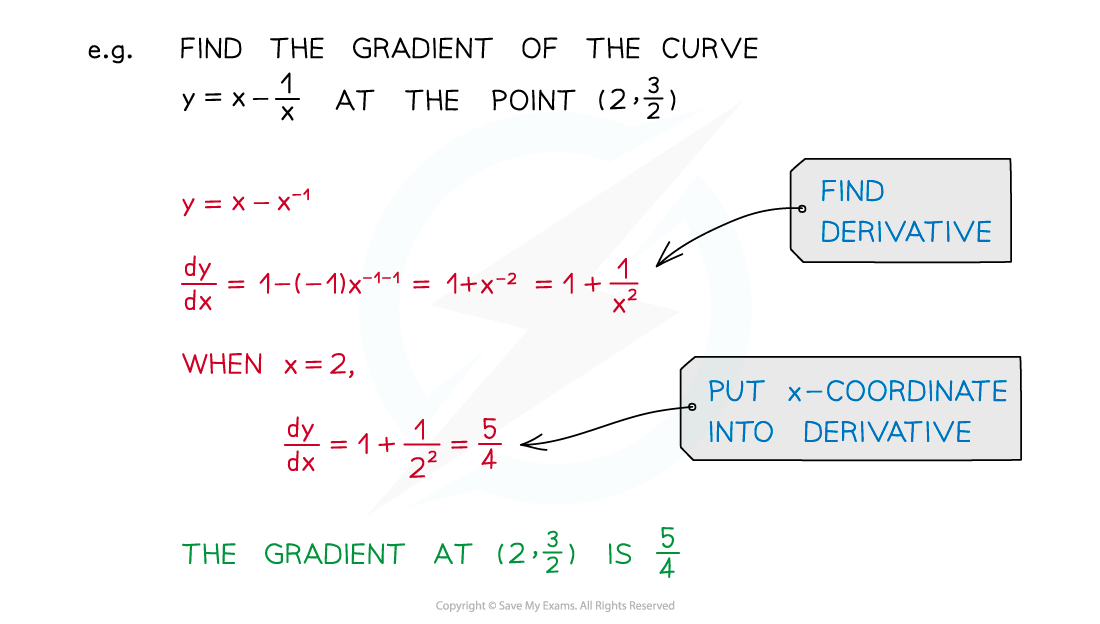
Using the derivative to find a tangent

• At any point on a curve, the tangent is the line that goes through the point and has the same gradient as the curve at that point

• For the curve y = f(x), you can find the equation of the tangent at the point (a, f(a)) using 

Using the derivative to find a normal

• At any point on a curve, the normal is the line that goes through the point and is perpendicular to the tangent at that point

• For the curve y = f(x), you can find the equation of the normal at the point (a, f(a)) using